14.0:　Realized causal observable in classical systems

Abstract (14.0:　Realized causal observable in classical systems )

Abstract: As mentioned in the previous chapters, what is important is

In this chapter, we discuss the relationship more systematically. That is, we add the further argument concerning the realized causal observable. This field is too vast, thus, we mainly concentrate our interest to classical systems, particularly, Zeno's paradox. That is,

$(\flat):$

to describe the flying arrow ( the best work in Zeno's paradoxes ) in terms of quantum language

We believe that this is the final answer to Zeno's paradox.

---

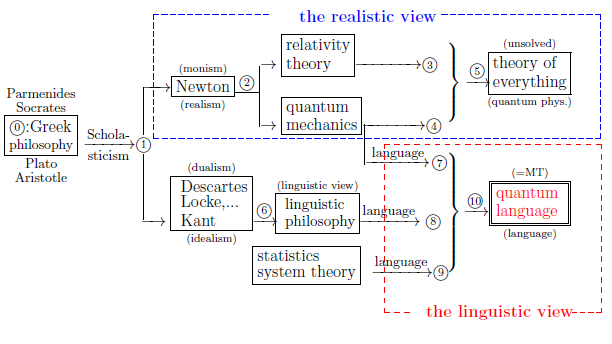
Again recall that, as mentioned in $\S$1.1, the main purpose of this book is to assert the following figure 1.1:

Fig.1.1: the location of "quantum language" in the world-views

This(particularly, ⑦--⑨) implies that quantum language has the following three aspects: $$ \left\{\begin{array}{ll} \mbox{ ⑦ :the standard interpretation of quantum mechanics} \\ \mbox{ $\qquad$ (i.e., the true colors of the Copenhagen interpretation) } \\ \\ \mbox{ ⑧ : the final goal of the dualistic idealism (Descartes=Kant philosophy) } \\ \\ \mbox{ ⑨ : theoretical statistics of the future } \end{array}\right. $$