言語ルール1の気分を感じるために, 簡単な例[コップの水は熱いか冷たいか]を示す.

  • 「この程度のことなんだ!!!」
と思ってもらえばよい.


["Cold or Hot" for water in a cup]
(量子言語の知識がなくても、読めるように以下を書いた)

いろいろな温度$\omega$℃ $(0 {{\; \leqq \;}}\omega {{\; \leqq \;}}100)$ のコップの水(お湯)を， 多くの被験者に 飲んでもらって，「熱いか？冷たいか？」を 二者択一のアンケート形式で質問する． そして，得られた データ(たとえば，$g_{冷}(\omega)$人が「冷たい」， $g_{熱}(\omega)$人が「熱い」と答えたとする) を正規化と，折れ線化により，以下の \begin{align} & f_{冷}(\omega)(=f_c(\omega )) = \frac{g_{冷}(\omega)}{被験者数} \\ & f_{熱}(\omega)(=f_h(\omega ))=\frac{g_{熱}(\omega)}{被験者数} \end{align} を得たとしよう．


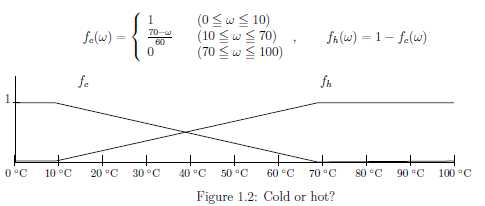
したがって, たとえば,,
$(A_1):$多くの被験者の中から一人を選んで，$55$℃のコップの水が 「熱いか？冷たいか？」を二者択一で質問すれば， その被験者が $ \left[\begin{array}{ll} \mbox{"cold"} \\ \mbox{"hot"} \end{array}\right] $と言う確率は$ \left[\begin{array}{ll} f_{\text c}(55)=0.25 \\ f_{\text h}(55)=0.75 \end{array}\right] $ である

この事実・現象を， 二元論的記述法(=測定理論的記述法=量子言語) で 記述することを以下に考える．

状態空間を$\Omega=区間[0, 100]$として， 測定値空間を$X=\{冷, 熱\}$とする． ここで， 次のような「冷熱-測定器」を考えよう:

$(A_2):$ $\left.\begin{array}{ll}\omega \\ \end{array}\right.$℃ の水に対して、 確率$ \left[\begin{array}{ll} f_{\text c}(\omega) \\ f_{\text h}(\omega) \end{array}\right] $ で $ \left[\begin{array}{ll} \mbox{c} \\ \mbox{h} \end{array}\right] $ を表示するような冷熱-測定器(=[C-H]-温度計)を考える． この 冷熱-測定器を ${\mathsf O} =$ $(f_{冷},f_{熱})$ と記す．
もちろん，このような 「冷熱-測定器」 を工学的に作ることは， 乱数発生回路を用いれば，容易である． ここで，
$(A_3):$ $\qquad$(A$_1$)$\Longleftrightarrow$(A$_2$)
と見なそう。

したがって, 日常言語の文言$(A_1)$を量子言語(=測定理論)に 翻訳 して、次を得る。

$(A_4):$ 55℃ (状態 $(=\omega =55 \in \Omega) )$の水に対して、 [C-H]-温度計(= 測定器 ${\mathsf O} =(f_{\text c},f_{\text h})$)で測定すれば、 測定値 $ \left[\begin{array}{ll} \mbox{c} \\ \mbox{h} \end{array}\right]$ を得る確率は $\left[\begin{array}{ll} f_{\mbox{c}}(55)=0.25 \\ f_{\mbox{h}}(55)=0.75 \end{array}\right]$ である。
すなわち、翻訳： $$ (A_1) \xrightarrow[翻訳]{}　(A_4) $$ を得た。
上は簡単すぎると思うかもしれない。「翻訳」だけでは、何も進展がないと思うかもしれない。



しかし、次章以降で、
  • 量子言語の記述力に驚愕してもらう
すなわち、
  • 量子言語が万能の呪文であることに納得してもらう
のが、 この講義の目的である。