であるが、このすこしの違い
「$\doteqdot$」
によって、量子言語は「言語的科学観」を主張できるようになる。
この意味で、この講義では「$=$」でなくて、
「$\doteqdot$」
の部分を強調することになる。
は気になる。
天才フォン・ノイマンは量子言語に限りなく接近したのに、そこに踏み込まなかった。
そうならば、
量子言語は、数学ではない。 「数学など、面倒!!」と思う向きは、数学をスキップして、2.5節から読み始めてもよい。
統計学と量子力学のたいていの書は、(数学でなくて)算数で書かれていて、それでも十分に役に立つ。
この事実を量子言語も見習うべきで、算数で書かれている量子言語の本が必要と思う。
本当に重要な所は数学ではないのだから、誰かにそういう本を書いてもらいたい。
 量子力学のヒルベルト空間による定式化はフォン・ノイマン(1903-1957)に拠る。
フォン・ノイマンのこの仕事の重要さは強調してもし過ぎることができないほど重要である。
物理学ならば、当然、微分積分学(やその一般化の微分幾何学)という数学で記述されると考えるのが普通であるが、
フォン・ノイマンは
量子力学のヒルベルト空間による定式化はフォン・ノイマン(1903-1957)に拠る。
フォン・ノイマンのこの仕事の重要さは強調してもし過ぎることができないほど重要である。
物理学ならば、当然、微分積分学(やその一般化の微分幾何学)という数学で記述されると考えるのが普通であるが、
フォン・ノイマンは
ことは、驚くべきことで、フォン・ノイマンにしかできなかったことと考える。
さて、
と量子言語を疑う気持ちにならない読者がいたとしたら、どうかしている。
この節ではヒルベルト空間論の初歩(大学3年程度)について復習しておく。
ヒルベルトは大数学者であるが、ヒルベルト空間について特出した業績があるわけではない。フォン・ノイマンは 「ヒルベルト空間」と名付けたが、「フォン・ノイマン空間」と名付けるべきであった。
2.1.1:ヒルベルト空間と作用素代数
複素数体を${\mathbb C}$として、 $H$を複素ヒルベルト空間とする。 内積 $\langle \cdot , \cdot \rangle : H \times H \to {\mathbb C} $ は次を満たすとする:
| $\bullet$ | ${\langle w, w \rangle} \ge 0 \; (\forall w \in H )$, $\qquad$ $\quad$ |
| $\bullet$ | ${\langle w, w \rangle}=0 \Leftrightarrow w=0$, |
| $\bullet$ | ${\langle w, \alpha_1 w_1 + \alpha_2 w_2 \rangle} = \alpha_1 {\langle w, w_1 \rangle}+ \alpha_2 {\langle w, w_2 \rangle} \quad (\forall w, w_1, w_2 \in H, \forall \alpha_1, \alpha_2 \in {\mathbb C})$, |
| $\bullet$ | ${\langle w_1, w_2 \rangle} = \overline{\langle w_2, w_1 \rangle}$ (i.e., 共役複素数) $(\forall w_1, w_2 \in H)$ |
ノルム$\| u \| $ (or $\|u \|_H $)を
$\| u \| =| \langle u , u \rangle|^{1/2} $で定義して、
バナッハ空間 $(H, \| \cdot \|)$を得る。
作用素空間$B(H)$
を次で定める:

作用素ノルム $\| \cdot \|_{B(H)}$を以下のように定めて、 $B(H)$をバナッハ空間と見なす:
\begin{align} \| T \|_{B(H)} = \sup_{\| x \|_H =1} \|T x \|_H \quad ( \forall T \in B(H) ) \tag{2.2} \end{align}さて、$T \in B(H)$としよう。$T$の 共役作用素 $T^* \in B(H)$を次のように定める:
\begin{align} \langle T^* u, v \rangle = \langle u, T v \rangle \quad (\forall u,v \in H) \end{align} 次は明らか: \begin{align}
(T^*)^* =T, \quad
(T_1 T_2 )^* = T_2^* T_1^*
\end{align}
\begin{align}
(T^*)^* =T, \quad
(T_1 T_2 )^* = T_2^* T_1^*
\end{align}
さらに, 次の等式(called "$C^*$-条件" )が成り立つ:
\begin{align} \|T^* T\|=\|T T^* \|=\|T\|^2=\|T^* \|^2 \quad (\forall T \in B(H)) \tag{2.3} \end{align}$T=T^*$が成り立つとき, $T$は 自己共役作用素 (or, エルミート作用素) と呼ばれる. $T_n (n \in {\mathbb N} =\{ 1,2, \cdots\} ),T \in B(H)$として、 点列$\{T_n \}_{n=1}^\infty $がノルム位相の意味で$T$へ収束するとは (すなわち, $(n)-\lim_{n \to \infty } T_n = T$), 次を満たすときを言う:
\begin{align} \lim_{n \to \infty} || T_n - T ||_{B(H)}=0 \end{align}また、$\{T_n \}_{n=1}^\infty $が$T$へ弱収束するとは (すなわち, $(w)-\lim_{n \to \infty } T_n = T$ ), 次を満たすときを言う:
\begin{align} \lim_{n \to \infty} \langle u, (T_n - T) u \rangle = 0 \qquad (\forall u \in H ) \tag{2.4} \end{align}$B(H)$内には様々な位相が考えられるが、 本書では、上の二つ(i.e.,ノルム収束と弱収束)だけを考える。
${\mathcal A} (\subseteq B(H) )$が次を満たすとき、 $C^*$-代数と呼ぶ。
| $(A_1):$ | ${\mathcal A} (\subseteq B(H) )$は、作用素ノルム$\| \cdot \|_{B(H)}$の意味で 閉部分空間: |
| $(A_2):$ | ${\mathcal A}$は$\ast$-代数, すなわち, 次を満たす。 \begin{align} F_1, F_2 \in {\mathcal A} \Rightarrow F_1 \cdot F_2 \in {\mathcal A}, \qquad F \in {\mathcal A} \Rightarrow F^* \in {\mathcal A} \end{align} |
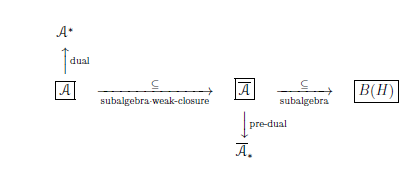
2.1.2 基本構造$[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]$;$\;\;$ 一般論
基本構造 $[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]$ $\Big($ or, denoted by $[{\mathcal A} \subseteq \overline{\mathcal A}]_{ B(H)}$ $\Big)$を考えよう. すなわち,
| $\quad$ | ${\mathcal A} ( \subseteq B(H))$は$C^*$-代数で、$\overline{\mathcal A} ( \subseteq B(H))$は${\mathcal A}$の弱閉包. $W^*$-代数 $\overline{\mathcal A}$は前共役バナッハ空間 $\overline{\mathcal A}_*$(よく知られた定理より、 $(\overline{\mathcal A}_*)^*=\overline{\mathcal A}$を一意に持つ。) |
- 一般基本構造:$[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]$
2.1.3: 基本構造$[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]$と状態空間;$\;\;$一般論
状態空間は, $C^*$代数${\mathcal A}$の共役空間${\mathcal A}^*$
(と
$W^*$代数$\overline{\mathcal A}$の前共役空間${\mathcal A}_*$
)の中で定義される.
以下の通りである.
 基本構造:
\begin{align}
[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]
\end{align}
を考えよう。
$C^*$-代数${\mathcal A}$の共役空間を${\mathcal A}^*$とする.
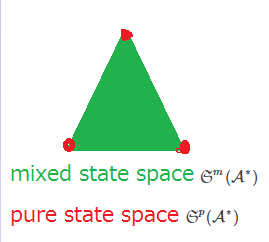
混合状態空間${\frak S}^m({\mathcal A}^*)$
と
純粋状態空間${\frak S}^p({\mathcal A}^*)$
を次のように定義する.
基本構造:
\begin{align}
[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]
\end{align}
を考えよう。
$C^*$-代数${\mathcal A}$の共役空間を${\mathcal A}^*$とする.
混合状態空間${\frak S}^m({\mathcal A}^*)$
と
純粋状態空間${\frak S}^p({\mathcal A}^*)$
を次のように定義する.
| (a): | ${\frak S}^m({\mathcal A}^*)=\{ \rho \in {\mathcal A}^* \;| \; \|\rho \|_{{\mathcal A}^*}=1, \rho \ge 0 \mbox{ (i.e., $\rho(T^* T) \ge 0 (\forall T \in {\mathcal A})$)}\}$ |
| (b): | ${\frak S}^p({\mathcal A}^*)=\{ \rho \in {\frak S}^m({\mathcal A}^*) \; | \; \rho \mbox{ は純粋状態} \}$. ここに, $\rho (\in {\frak S}^m({\mathcal A}^*))$が純粋状態であるとは, 次を満たすことである. \begin{align} \rho = \alpha \rho_1 + (1-\alpha ) \rho_2, \rho_1 , \rho_2 \in {\frak S}^m({\mathcal A}^*), 0 < \alpha <1 \Longrightarrow \rho=\rho_1=\rho_2 \end{align} |
また,$\overline{\mathcal A}$の前共役空間を$\overline{\mathcal A}_*$とする. このとき,もう一つの 混合状態空間 $\overline{\frak S}^m(\overline{\mathcal A}_*)$}を次のように定める.
| (c): | $\overline{\frak S}^m({\overline{\mathcal A}}_*) =\{ \rho \in {\overline{\mathcal A}}_* \;| \; \|\rho \|_{\overline{\mathcal A}_*}=1, \rho \ge 0 \mbox{ (i.e., $\rho(T^* T) \ge 0 (\forall T \in \overline{\mathcal A})$)}\}$ |
上で,二つの混合状態空間を区別したい場合は, $C^*$-混合状態空間${\frak S}^m({\mathcal A}^*)$と $W^*$-混合状態空間$\overline{\frak S}^m({\overline{\mathcal A}}_*)$ のように呼ぶ.
以上を,図式でまとめて,次のようになる.- 一般基本構造:$[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]$と状態空間
| (D): | $ \left\{\begin{array}{ll} \mbox{フィッシャー統計学} & \cdots \mbox{純粋状態空間:}{{\frak S}^p({\mathcal A}^*)} \textcolor{blue}{\mbox{: most fundamental }} \\ \\ \mbox{ベイズ統計学} & \cdots \left\{\begin{array}{ll} \mbox{{$C^*$-混合状態空間:}${{\frak S}^m({\mathcal A}^*)}$} \textcolor{blue}{\mbox{: easy }} \\ \\ \mbox{{$W^*$-混合状態空間:}${\overline{\frak S}^m(\overline{\mathcal A}_*)}$} \textcolor{blue}{\mbox{: natural, useful }} \end{array}\right. \end{array}\right. $ |