数学系の学科の3,4年で履修することであるが、
ヒルベルト空間論は「行列(線形代数):$(\flat_2)$」の無限次元版で、
量子系の場合には, 基本構造$[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]$は次のようになる。
以下の定理 2.6と2.7で、"コンパクト作用素クラス ${\mathcal C}(H)$"と"トレースクラス${\mathcal Tr}(H)$"を説明するが、
その前に、"ディラック記号"と"CONS"について述べておく。
$u, v \in H$として,
$| u \rangle \langle v | \in B(H)$を以下のように定める.
\begin{align}
(| u \rangle \langle v |)w = \langle v , w \rangle u
\quad (\forall w \in H)
\tag{2.9}
\end{align}
ここで,
$\langle u |$をブラ・ベクトル,
$| u \rangle$をケット・ベクトルと呼ぶ.
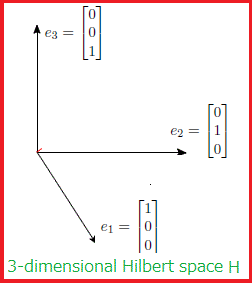
ヒルベルト空間$H$内の
点列$\{e_k\}_{k=1}^\infty$
は、次を満たすときONS(orthonormal system;正規直交系)
と呼ばれる:
さらに、
ONS
$\{e_k\}_{k=1}^\infty$
が次を満たすとき、CONS(complete orthonormal system;完全正規直交系)
と呼ばれる:
となる.
しかし,
空間(集合)は同じであるが,
ノルムは,上記の($C_3$)と($D_3$)のように異なるので,注意しなければならない.
理工系の大学一年の数学は、「微積分」と「行列(線形代数)」の二本立てになっている
と進み、
$(\flat_1)$
「微積分」は、
[偏微分・重積分]$\longrightarrow$[ベクトル解析(ストークスの定理、ガウスの発散定理(微分幾何)]
と進んだのであった。
$(\flat_2)$
「行列(線形代数)」は、
[有限次元ベクトル空間]$\longrightarrow$[行列(=線形写像)]$\longrightarrow$[対角化定理]
と進む。したがって、「$(\flat_2) \doteqdot (\flat_3)$」と思っていいだろう。
$(\flat_3)$
「ヒルベルト空間論」は、
[無限次元ベクトル空間]$\longrightarrow$[線形写像]$\longrightarrow$[対角化定理(=スペクトル分解定理)]
ここで、次の疑問は当然だろう
この答えとしては、「昔からそうだから」とか「世界的にそうだから」としか、大学教員も答えられないかもしれないが、世界記述的(本書的)観点からいえば
$$
\begin{cases}
\mbox{「微積分(微分幾何学)」} & \cdots \cdots 相対性理論(実在的科学観)
\\
\mbox{「行列(線形代数・ヒルベルト空間論)」} & \cdots \cdots 量子力学(言語的科学観)
\end{cases}
$$
同じ意味で、はっきり言ってしまうと、
$$
\begin{cases}
(\flat_1) \doteqdot \mbox{電磁気学}
\\
(\flat_2) \doteqdot \mbox{量子力学}
\end{cases}
$$
であって、標語的に言えば、
$(\flat_4)$
数学には、代数とかいろいろあるのに、なぜ「微積分」と「行列(線形代数)」を大学一年で学ぶのだろうか?
である。
2.2.1: 量子系の基本構造$[{\mathcal C}(H) \subseteq B(H) \subseteq B(H)]$: コンパクト作用素, トレース作用素
\(\require{AMScd}\)
\begin{align}
\begin{CD}
{\mathcal Tr}(H)
@.
@.
\\
@AA{\mbox{ dual}}A
@.
\\
\quad \fbox{${\mathcal C}(H)$} \quad
@>{\subseteq}>\mbox{ subalgebra$\cdot$weak-closure}>
\quad \fbox{$B(H) $}\quad
@>{\subseteq}>\mbox{ subalgebra}>
\quad
\fbox{${B(H)}$}\quad
\\
@.
@VV{\mbox{ pre-dual}}V
\\
@.
{\mathcal Tr}(H)
@.
\\
\tag{2.8}
\end{CD}
\end{align}
ここで、"コンパクト作用素クラス ${\mathcal C}(H)$"と"トレースクラス${\mathcal Tr}(H)$"は、以下に説明する。
 定義2.5 [(i): ディラック記号]
定義2.5 [(i): ディラック記号]
$(\sharp)$ $\langle e_k, e_j \rangle = \left\{\begin{array}{ll}
1 \quad & (k = j )
\\
0 \quad & (k \not= j )
\end{array}\right.
$
$(\sharp)$
$\langle x, e_k \rangle =0
\;
(\forall k=1,2,...)$
$\;\; \Longrightarrow \;\;$
$x=0$.
簡単のため,以下での「$B(H)$内
での収束」は「弱収束」とする.
${\mathcal C}(H) (\subseteq B(H))$をコンパクト作用素全体の空間とする.
このとき,
次の($C_1$)-($C_4$)(
特に,
($C_1$)$\leftrightarrow$
($C_2$)
)
が,成立する.

$(C_1):$
$T \in {\mathcal C}(H)$. ここで,$T ( \in B(H) )$がコンパクト作用素であるとは,
ヒルベルト空間$H$内の点列
$\{u_n \}_{n=1}^\infty$が有界列ならば,
$\{Tu_n \}_{n=1}^\infty$は収束する部分列を持つ
ことである。
$(C_2):$
ヒルベルト空間$H$内に二つの正規直交系
$\{e_k\}_{k=1}^\infty$
と
$\{f_k\}_{k=1}^\infty$
と
$\lim_{k \to \infty } \lambda_k =0$なる
非負数列$\{\lambda_k \}_{k=1}^\infty$を定めて
\begin{align}
T=\sum_{k=1}^\infty \lambda_k |e_k \rangle \langle f_k|
%\quad \mbox{()}
\tag{2.10}
\end{align}
と表現できる.
$(C_3):$
コンパクト作用素の空間
${\mathcal C}(H)( \subseteq B(H))$は
$C^*$-代数で,$T (\in {\mathcal C}(H))$を($C_2$)のように表現したとき,
\begin{align}
\| T \|_{B(H)}= \max_{k=1,2, \cdots } \lambda_k
\tag{2.11}
\end{align}
と計算できる.
$(C_4):$
コンパクト作用素の空間${\mathcal C}(H)$の弱閉包は,
$B(H)$となる. すなわち,
\begin{align}
\overline{{\mathcal C}(H)}=B(H)
\tag{2.12}
\end{align}
 定理 2.7 [トレースクラス${\mathcal Tr}(H)$の性質]
定理 2.7 [トレースクラス${\mathcal Tr}(H)$の性質]
簡単のため,以下での収束は「弱収束」とする.
次の($D_1$)-($D_4$)が,成立する.
($D_1$)と($D_2$)は同値として,すなわち,
${\mathcal Tr}(H)$(トレース作用素全体の空間)の定義を
($D_2$)とする.
$(D1):$ $T (\in {\mathcal C}(H) \subseteq B(H))$をトレース作用素とする. すなわち,
$T \in {\mathcal Tr}(H)$
$(D2):$ ヒルベルト空間$H$内に二つの正規直交系
$\{e_k\}_{k=1}^\infty$
と
$\{f_k\}_{k=1}^\infty$
と
$\sum_{k=1}^\infty \lambda_k < \infty$なる
正数列$\{\lambda_k \}_{k=1}^\infty$を定めて
\begin{align}
T=\sum_{k=1}^\infty \lambda_k |e_k \rangle \langle f_k|
%\quad \mbox{()}
\end{align}
と表現できる.
$(D3):$
トレース空間
${\mathcal Tr}(H)( \subseteq B(H))$は,コンパクト作用素の空間${\mathcal C}(H)( \subseteq B(H))$の共役バナッハ空間である.すなわち,
\begin{align}
{\mathcal C}(H)^*={\mathcal Tr}(H)
\tag{2.13}
\end{align}
さらに,
共役ノルム$\| \cdot \|_{{\mathcal C}(H)^*}$はトレースノルムと呼ばれ,
$\| \cdot \|_{tr}$と記されて,
\begin{align}
\|T\|_{tr}= \sum_{k=1}^\infty \lambda_k
\tag{2.14}
\end{align}
となる.
$(D4):$
トレース空間
${\mathcal Tr}(H)( \subseteq B(H))$の共役バナッハ空間は,
$B(H)$となる.
すなわち,
\begin{align}
{\mathcal Tr}(H)^*=B(H)
\qquad
\mbox{ 同じ意味で,}
\qquad
{\mathcal Tr}(H)=B(H)_*
\tag{2.15}
\end{align}
となる.
2.2.2 量子系の基本構造$[{\mathcal C}(H) \subseteq B(H) \subseteq B(H)]$と状態空間e
量子系の基本構造:
\begin{align}
[{\mathcal C}(H) \subseteq B(H) \subseteq B(H)]
\end{align}
と次の図式を考えよう
\begin{align}
&
\begin{array}{rlrlll}
\underset{{{\mbox{ $C^*$-純粋状態}}}}{
{{\frak S}^p({\mathcal Tr}(H))}}
\subset \underset{{\mbox{ $C^*$-混合状態}}}{
{{\frak S}^m({\mathcal Tr}(H))}}
\subset
&
{\mathcal Tr}(H) &&&&
\\
&
\Big\uparrow \mbox{ dual}
&&&&
\\
&
\fbox{$
{\mathcal C}(H)$}
&
\xrightarrow[\mbox{ subalgebra$\cdot$weak-closure}]{\subseteq}
&
\fbox{${B(H)}$}
&
\xrightarrow[\mbox{ subalgebra}]{\subseteq}
\fbox{${B(H)}$}
&
\\
& &&
\Big\downarrow \;\mbox{ pre-dual}
&&
\end{array}
\\
&
\qquad \qquad \qquad \qquad \qquad \qquad
\qquad \qquad \qquad \qquad \qquad \qquad
\underset{{\mbox{ $W^*$-混合状態}}}{\overline{\frak S}^m({\mathcal Tr}(H))} \subset
{\mathcal Tr}(H)
\nonumber
\end{align}
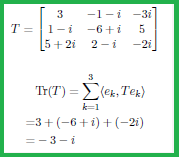 定義2.9 [Tr: トレース].
トレース${\mbox{Tr}}: {\mathcal Tr}(H) \to {\mathbb C}$
を次のように定める。
\begin{align}
{\mbox{Tr}}(T)
=
\sum_{n=1}^\infty \langle e_n, T e_n \rangle
\qquad (\forall T \in {\mathcal Tr}(H) )
\tag{2.23}
\end{align}
ここで、$\{e_n\}_{n=1}^\infty $はヒルベルト空間$H$内のCONS(完全正規直交系)。
${\mbox{Tr}}(T)$の値はCONS
$\{e_n\}_{n=1}^\infty $の選び方に依存しない。
また、次は頻繁に使う:
\begin{align}
_{_{{\mathcal Tr}{(H)}}}\Big(
|u \rangle \langle u |,
F
\Big)
{}_{_{B(H)}}
=
{\mbox{Tr}}
(
|u \rangle \langle u |
\cdot
F
)
=
\langle u, F u \rangle
\quad
(\forall ||u||_H=1, F \in B(H)
)
\tag{2.24}
\end{align}
定義2.9 [Tr: トレース].
トレース${\mbox{Tr}}: {\mathcal Tr}(H) \to {\mathbb C}$
を次のように定める。
\begin{align}
{\mbox{Tr}}(T)
=
\sum_{n=1}^\infty \langle e_n, T e_n \rangle
\qquad (\forall T \in {\mathcal Tr}(H) )
\tag{2.23}
\end{align}
ここで、$\{e_n\}_{n=1}^\infty $はヒルベルト空間$H$内のCONS(完全正規直交系)。
${\mbox{Tr}}(T)$の値はCONS
$\{e_n\}_{n=1}^\infty $の選び方に依存しない。
また、次は頻繁に使う:
\begin{align}
_{_{{\mathcal Tr}{(H)}}}\Big(
|u \rangle \langle u |,
F
\Big)
{}_{_{B(H)}}
=
{\mbox{Tr}}
(
|u \rangle \langle u |
\cdot
F
)
=
\langle u, F u \rangle
\quad
(\forall ||u||_H=1, F \in B(H)
)
\tag{2.24}
\end{align}
2.2: 量子系の基本構造 $[{\mathcal C}(H) \subseteq$ $ B(H) \subseteq B(H)]$
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
定理 2.6 [コンパクト作用素クラス ${\mathcal C}(H)$の性質]
