基本構造$[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]$は,
古典系では,
古典系の$C^*$代数は, 可換$C^*$代数${{\mathcal A}} =C_0(\Omega)$と見なせる.
ここに, $\Omega$は局所コンパクト空間であるが, 具体的には,
たとえば, $\Omega$として,
局所コンパクト空間$\Omega$上の関数空間$C_0(\Omega)$を次のように定義する.
ここに, 「$\lim_{\omega \to \infty} f(\omega)=0$」の意味は,
したがって, $\Omega$がコンパクトならば, 条件「$\lim_{\omega \to \infty} f(\omega)=0$」は不要で, $C_0(\Omega)$を$C(\Omega)$と記すことが普通である.
ただし,本書では,$\Omega$がコンパクトでも$C_0(\Omega)$と記すことが多々ある.
複素ベクトル空間$C_0(\Omega)$のノルム$\| \cdot \|_{C_0(\Omega )}$を
\begin{align}
\| f \|_{C_0(\Omega )}= \max_{\omega \in \Omega } |f(\omega)|
\tag{2.31}
\end{align}
と定めて, バナッハ空間$( C_0(\Omega) ,\| \cdot \|_{C_0(\Omega )} )$を得る.
さて,$\Omega$を
局所コンパクト空間として,
測度空間$(\Omega, {\cal B}_{\Omega}, \nu)$を考える.
ここで,
${\cal B}_{\Omega}$
はボレル集合体,
すなわち,
$\Omega$内の
すべての開集合を含む最小の$\sigma$-集合体とする.
更に,
次を仮定する:
バナッハ空間
$L^r (\Omega, \nu)$
(ここで,
$r = 1, 2, \infty $)
を
複素数値可測関数$f: \Omega\to {\mathbb C}$
で,
$\|f\|_{L^r (\Omega, \nu)} < \infty$
を満たす関数全体とする.
ここで,
関数$f$の
ノルム
$\|f\|_{L^r (\Omega, \nu)} $
は
$L^r (\Omega, \nu)$
は,
略して
$L^r (\Omega)$
$($
または,詳しくは$L^r (\Omega, {\cal B}_{\Omega}, \nu)$
$)$
と記すこともある.
次は, 可換$C^*$代数$( C_0(\Omega) ,\| \cdot \|_{C_0(\Omega )} )$の共役バナッハ空間$( C_0(\Omega)^* ,\| \cdot \|_{C_0(\Omega )^*} )$について考える. リースの定理によって,
である.
したがって, $F \in C_0(\Omega)$, $\rho \in C_0(\Omega)^*={\mathcal M}(\Omega)$のとき, 双線形形式はいろいろな表現ができる. たとえば,
ここに,
$\Xi^c$は$\Xi$の補集合で, $Re(z)$="複素数$z$の実部",
$Im(z)$="$z$の虚部"とする.
古典系の基本構造 $[C_0(\Omega ) \subseteq L^\infty (\Omega, \nu ) \subseteq {B(L^2( \Omega, \nu ))}]$を考えよう.
このとき, 状態空間としては,次の図式を得る.
となる.
ここで, 点$\omega_0(\in \Omega)$での
点測度
$\delta_{\omega_0}\in {\mathcal M}(\Omega)$は次を満たす測度である.
注意2.13[有限集合$\Omega$について:
$C_0(\Omega)=L^\infty(\Omega,\nu)$,
${\mathcal M}(\Omega ) = L^1(\Omega, \nu )$
]
2.3.1 古典系の基本構造$[C_0(\Omega ) \subseteq L^\infty (\Omega, \nu ) \subseteq {B(L^2( \Omega, \nu ))}]$
以下に,この図式を説明する.
2.3.1.1 可換$C^*$-代数 $C_0(\Omega)$
(B):
任意の$\epsilon >0$に対して, 次を満たすコンパクト集合$K (\subseteq \Omega)$が存在する:
\begin{align}
\{ \omega \;|\; \omega \in \Omega \setminus K, |f(\omega)| > \epsilon \}
=
\emptyset
\end{align}
たとえば,,
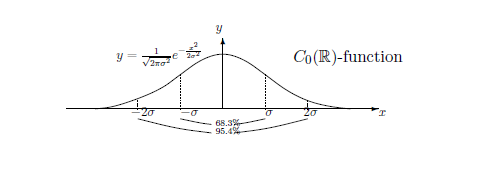
(C):
任意の開集合$U \subseteq \Omega$
に対して,$0 < \nu (U) {\; \leqq \;} \infty$
が成立する.
また,
測度$\nu$
は
$\sigma$-有限
とする
$\fbox{注釈2.1}$
コンパクト化(Stone-Cechコンパクト化)して,
$\Omega$を
コンパクト空間とすると、理論的にはスッキリするが、本書ではそうしない。
また,
測度$\nu$は
有限測度
としても一般性を損なわない.
たとえば,
$\nu(\Omega)=1$としてもよい.
したがって,
\begin{align}
\lim_{n \to \infty }
|
\Big\langle
\phi,
(f-f_n) \phi \Big\rangle_{L^2(\Omega, \nu )}
|
\le
&
\lim_{n \to \infty } \int_\Omega
|f_n(\omega ) - f(\omega ) |
\cdot
|
\phi ( \omega )|^2 \nu (d \omega )
\\
=
&
0
\qquad \qquad
(\forall \phi \in L^2 ( \Omega , \nu ))
\end{align}
だから,
\begin{align}
\mbox{$C_0(\Omega )$の弱閉
=
$L^\infty ( \Omega, \nu )$
}
\end{align}
よって、次の古典系の基本構造を得る:
\begin{align}
[
C_0(\Omega )
\subseteq L^\infty (\Omega )
\subseteq
B(L^2( \Omega, \nu ) )
]
\tag{2.38}
\end{align}
2.3.2 古典系の基本構造$[C_0(\Omega ) \subseteq L^\infty (\Omega, \nu ) \subseteq {B(L^2( \Omega, \nu ))}]$と状態空間
純粋状態空間${\frak S}^p(C_0(\Omega)^*)$は,
\begin{align}
{\frak S}^p(C_0(\Omega)^*)
&
=
\{ \rho=\delta_{\omega_0} \in {\frak S}^p(C_0(\Omega)^*) \;:\; \delta_{\omega_0}
\mbox{は点$\omega_0(\in \Omega)$での点測度}, \omega_0 \in \Omega\}
\nonumber
\\
&
\equiv
{\mathcal M}_{+1}^p(\Omega)
%\\
%=
%&
%%{\frak S}^m(C_0(\Omega))
%%=
%\{ \rho \in {\mathcal M}(\Omega) \;:\; \rho \mbox{は$\Omega$上の確率測度
%}\}
\tag{2.41}
\end{align}
$\Omega$を有限集合$\{\omega_1,\omega_2,...,\omega_n \}$とする。
離散距離$d_D$
と個数測度
$\nu$、
すなわち、
\begin{align}
\nu( D )= \sharp [D]
(=
\mbox{"$D$の要素の個数"}
)
\end{align}
とする。
このとき次は明らか:
\begin{align}
C_0(\Omega ) = \{ F : \Omega \to {\mathbb C} \;|\;
\mbox{ $F$は$\Omega$上の複素数値関数}
\}
=
L^\infty (\Omega, \nu )
\end{align}
また、
\begin{align}
&
\rho \in {\mathcal M}_{+1}(\Omega )
\;\;
\Longleftrightarrow
\;\;
\rho = \sum_{k=1}^n p_k \delta_{\omega_k }
\;\;( \sum_{k=1}^n p_k=1, p_k \ge 0)
\end{align}
そして
\begin{align}
&
f \in L^1_{+1}(\Omega, \nu )
\;\;
\Longleftrightarrow
\;\;
\sum_{k=1}^n f(\omega_k ) =1.
\;\;
f(\omega_k )\ge 0
\end{align}
したがって、次の同一視を得る:
\begin{align}
{\mathcal M}_{+1}(\Omega )
=
L^1_{+1}(\Omega, \nu )
\quad
(\mbox{ or, }
{\mathcal M}(\Omega )
=
L^1 (\Omega, \nu )
)
\end{align}
結局、
\begin{align}
C_0(\Omega )=
L^\infty(\Omega)
=
{\mathbb C}^n
\qquad
{\mathcal M}(\Omega )=
L^1(\Omega)
=
{\mathbb C}^n
\tag{2.44}
\end{align}
を得る。
ここに、
ノルム
$\| \cdot \|_{C_0(\Omega )}$
は
\begin{align}
\| z \|_{C_0(\Omega )}= \max_{k=1,2,...,n} |z_k |
\qquad
\forall z= \left[\begin{array}{l}
z_1
\\ z_2
\\
\vdots
\\
x_n \end{array}\right]
\in {\mathbb C}^n
\tag{2.45}
\end{align}
で定まり、
ノルム
$\| \cdot \|_{{\mathcal M}(\Omega )}$
は
\begin{align}
\| z \|_{{\mathcal M}(\Omega )}= \sum_{k=1}^n |z_k |
\qquad
\forall z= \left[\begin{array}{l}
z_1
\\ z_2
\\
\vdots
\\
x_n \end{array}\right]
\in {\mathbb C}^n
\tag{2.46}
\end{align}
2.3: 古典系の基本構造 $[C_0(\Omega ) \subseteq$ $ L^\infty ( \Omega, \nu ) \subseteq B(L^2 ( \Omega, \nu ))]$
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
(A): 古典系の基本構造: $[C_0(\Omega ) \subseteq L^\infty (\Omega, \nu )
\subseteq {B(L^2( \Omega, \nu ))}]$
\(\require{AMScd}\)
\[
\begin{CD}
{\mathcal M}(\Omega)
@.
@.
\\
@AA{\mbox{ dual}}A
@.
\\
\quad
\fbox{$C_0(\Omega)$}
\quad
@>{\subseteq}>\mbox{ subalgebra$\cdot$weak-closure}>
\quad \fbox{$ L^\infty(\Omega, \nu )$} \quad
@>{\subseteq}>\mbox{ subalgebra}>
\quad
\fbox{$ B(L^2(\Omega, \nu ))$}
\quad
\\
@.
@VV{\mbox{ pre-dual}}V
\\
@.
L^1(\Omega, \nu )
@.
\\
\end{CD}
\]
注意2.11
[$C_0(\Omega )\subseteq
B(L^2( \Omega, \nu ) )$」の見方]
ヒルベルト空間$H$を
\begin{align}
H=L^2( \Omega, \nu )
\end{align}
とする.
$f \in C_0(\Omega ) $に対して,
$T_f \in B(L^2( \Omega, \nu ) )$
を
\begin{align}
L^2( \Omega, \nu )
\ni \phi \longrightarrow T_f( \phi) = f \cdot \phi \in L^2( \Omega, \nu )
\tag{2.33}
\end{align}
と定めて,次の同一視:
\begin{align}
C_0(\Omega )
\ni f \underset{同一視}{\longleftrightarrow} T_f
\in B(L^2( \Omega, \nu ) )
\end{align}
の下に,
\begin{align}
f
\in C_0(\Omega )
\subseteq
B(L^2( \Omega, \nu ) )
\tag{2.34}
\end{align}
と見る.
定理 2.12 [ゲルファントの定理]
一般基本構造:
\begin{align}
[
{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)
]
\end{align}
において、
${\mathcal A} $は可換$C^*$-代数とする。
このとき、
次を満たす測度空間
$(\Omega, {\mathcal B}_\Omega, \nu )$
(ここに$\Omega$は局所コンパクト空間)
が存在する:
\begin{align}
{\mathcal A}=C_0(\Omega ),
\;\;
\overline{\mathcal A}=L^\infty (\Omega, \nu ),
\;\;
B(H)=B(L^2 (\Omega, \nu ))
\end{align}
このとき、$\Omega$は
スペクトラム
と呼ばれる.
(D):古典系の基本構造と状態空間
\begin{align}
&
\begin{array}{rlrlll}
\underset{{\mbox{ $C^*$-純粋状態}}}{
{\underset{(\approx \Omega )}{{\mathcal M}_{+1}^p (\Omega )}}
} \subset
\underset{{\mbox{ $C^*$-混合状態}}}{\underset{\mbox{ (probability measure)}}{{{\mathcal M}_{+1} (\Omega )} }}\subset
&
{\mathcal M}(\Omega ) &&&&
\\
&
\Big\uparrow \mbox{ dual}
&&&&
\\
&
\fbox{$
C_0(\Omega ) $}
&
\xrightarrow[\underset{\mbox{ weak-closure}}{\mbox{ subalgebra}}]{\subseteq}
&
\fbox{$L^\infty ( \Omega) $}
&
\xrightarrow[\mbox{ subalgebra}]{\subseteq}
\fbox{${B(L^2( \Omega))}$}
&
\\
& &&
\;\;\;
\Big\downarrow \;\mbox{ pre-dual}
&&
\end{array}
%\tag{2.39}
\\
& \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad
\underset{{\mbox{ $W^*$-混合状態}}}{\underset{\mbox{ (probability density function)}}{{L^1_{+1}( \Omega, \nu )}}} \subset
L^1( \Omega, \nu )
\end{align}
混合状態空間${\frak S}^m(C_0(\Omega)^*)$は,
\begin{align}
{\frak S}^m(C_0(\Omega)^*)
=
&
\{ \rho \in {\mathcal M}(\Omega) \;:\; \rho \ge 0, ||\rho||_{{\mathcal M}(\Omega)}=1\}
\nonumber
\\
=
&
%{\frak S}^m(C_0(\Omega))
%=
\{ \rho \in {\mathcal M}(\Omega) \;:\; \rho \mbox{は$\Omega$上の確率測度
}\}
\nonumber
\\
=:
&
{\mathcal M}_{+1} (\Omega )
\tag{2.40}
\end{align}
となる.
