前節では、上の$(\sharp_1)$を議論した。
上で、「システム(system)」はニュートン力学の「質点(point mass」と思えば、理解しやすいだろう。
また、統計学の母集団(population)の説明で、上表ほど分かり易い説明を著者は知らない。
たとえば,
第1章の図1.2
を見れば,
$\big( f_{冷}, f_{熱} \big)$
は,
「冷たい」と「熱い」という言葉の
仕切りを表しているとも言える.
測定器は,
「言葉の仕切り」を測定する装置
(すなわち,
仕切られた言葉たちから,一つの言葉を
選び出す装置)
である.
したがって,気分的には
「観測量$\not=$測定器」
であるが,本質的には同じものと考えてよい。
また,イギリス経験論の父であるジョン・ロック(1632年--1704年
)のアイデアとされている
「第一次性質」と「第二次性質」
は有名であるが(高校の「倫理」の教科書参照),これらのそれぞれが
測定理論の
「状態」と「観測量」に
対応していると思えばよい.
もちろん,
哲学的疑問($C_1$)を次の数学の問い掛け($C_3$)と関連させたい.
で, これならば, 「計算がドンドン進む」ことを期待できる.
この対応が, 「量子言語」として成功したと認められるとすれば,
疑問($C_1$)の「真の答え」は, 「常識的な($C_2$)」ではなくて,
2.4.1 二元論 (John Locke)
当面の目的は, 言語ルール1(測定:$\S$2.7))を「丸暗記」することである.
このためには、次の「基本構造、状態空間、観測量」等の数学的定義を理解しなければならない。
$(\sharp_1):$ 基本構造$[ {\mathcal A} \subseteq \overline{\mathcal A}]_{B(H)}$, 状態空間 ${\frak S}^p({\cal A}^*)$
$(\sharp_2):$ 観測量 ${\mathsf O}{{=}} (X, {\cal F} , F)$, etc.
 本節では、$(\sharp_2)$, i.e.,
本節では、$(\sharp_2)$, i.e.,
を議論する。
「状態」と「観測量(=測定器)」の二つは, ジョン・ロック(J. Locke)の「第一次性質」と「第二次性質」に対応する概念, すなわち,
\begin{align}
\left\{\begin{array}{ll}
\mbox{[状態(state)]} & \longleftrightarrow \mbox{[第一次性質(pimary quality)]}
\\
\mbox{[観測量(observable)]} & \longleftrightarrow \mbox{[第二次性質(secondary quality)]}
\end{array}\right.
\tag{2.47}
\end{align}
であり, したがって、
である.
また、次の表は「量子言語のキーワードと他の世界記述法のキーワード」の関係を理解し易くするだろう。

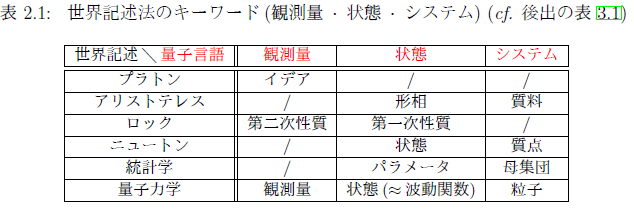
「存在論」という分野のことに精通しいるわけではないが、各世界記述法において、
「キーワードは存在している」と見なすのだと考える。
$\fbox{注釈2.2}$
「観測量(=測定器)」
について多少のことを説明しておく.
「観測量=言葉の仕切り」
と思えばよい.すなわち、
\begin{align}
\mbox{
"観測量" ="言葉の仕切り"="第二次性質"
}
\tag{2.48}
\end{align}
からである.一見、幼稚と思える概念が有名だとしたら、それにはそれなりの理由がある。
この言葉が
二元論の根幹を形成している
2.4.2 二元論 (in philosophy)と共役(in mathematics)
哲学のことをよく知っているわけではないが, やはり, 次の疑問:
は気にかかる.
常識的な答えは,
$(C_1):$ 失敗の連続であったにもかかわらず,
哲学者たちは、何故「二元論」に拘るのか?
だと思う. しかし、こんな答えで満足していたのでは、失敗の連鎖は断ち切れないと思う。
$(C_2):$ 「我」は特別なのもで,「世界」と一線を画したい
数学には, 「何故?」という疑問は原理的に無いわけで, 結果論的な答えしかない. すなわち
$(C_3):$ 関数空間${\mathcal A}$を考えたとき, 何故その共役空間${\mathcal A}^*$を考えるのか?
からである.
そうならば,
ジョン・ロックの二元論の根幹を形成する概念(「第一次性質」と「第二次性質」)に
共役関係を関連付けたくなる.
すなわち、
\begin{align}
\left\{\begin{array}{ll}
\mbox{[第一次性質]} & \longleftrightarrow \mbox{共役空間${\mathcal A}^*$内の[状態]}
\\
\mbox{[第二次性質]} & \longleftrightarrow \mbox{$C^*$代数${\mathcal A}$内
(計算の都合で,$W^*$代数$\overline{\mathcal A}$内)の[観測量]}
\end{array}\right.
\end{align}
(D): 共役空間${\mathcal A}^*$を考えると, 計算がドンドン進む
ということになる. このことを,
哲学者たちの鋭い嗅覚が感じ取っていたから,「二元論」に拘ったのだと思う.
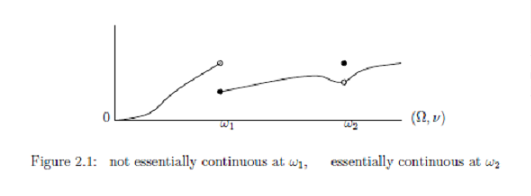
2.4.3 本質的 連続
2.1.2節では, 次の図式を述べた.| (F1): | もし$\rho$ $( \in {\overline{\frak S}^m(\overline{\mathcal A}_*)})$ が $\rho_0 (\in {\frak S}^p ({\cal A}^*))$ に弱収束すれば (すなわち, $\rho(G) \xrightarrow[\quad]{} \rho_0 (G) $ $ $ $(\forall G \in {\cal A} (\subseteq \overline{\cal A} )$ ), $\rho(F)$ は $\alpha $ に収束する |
もちろん, $F \in {\mathcal A}$は, $\rho_0 (\in {\frak S}^p ({\cal A}^*))$ で 本質的に連続 である.
注意2.1 [本質的連続(量子系と古典系)] [I]: 基本構造が $[{\mathcal C}(H) \subseteq B(H)]_{B(H)}$となる 量子系 では,
\begin{align} ({\mathcal C}(H))^*= {\mathcal Tr(H)} = B(H)_* \end{align}なので,$\rho \in {\frak S}^p({\mathcal C}(H)^*) \subseteq {\mathcal Tr}(H)$, $F \in \overline{{\mathcal C}(H)}=B(H)$となり,
\begin{align} \rho(G)= _{{\mathcal Tr}(H)} \Big( \rho, F )\Big)_{B(H)} \tag{2.51} \end{align} はいつも定義可能で,「本質的連続」は,「連続」と同値になる.[II]: また, 古典系 の基本構造 $[C_0(\Omega ) \subseteq L^\infty (\Omega, \nu ) \subseteq B(L^2 (\Omega, \nu ))]$を考えよう. 関数 $F$ $( \in L^\infty ( \Omega, \nu ))$ が 「 点$\omega_0$ $( \in \Omega = {\frak S}^p(C_0(\Omega )^*) )$ で本質的連続」 であるとは, 次の条件($F_2$)を満たす ことである:
| (F2): | もし $\rho_n (\in L_{+1}^1(\Omega, \nu )$ が \begin{align} \lim_{n \to \infty } \int_\Omega G(\omega ) \rho_n(\omega) \nu (d \omega ) =G(\omega_0) \qquad (\forall G \in C_0(\Omega ) ) \end{align} を満たすならば, \begin{align} \lim_{n \to \infty } \int_\Omega F(\omega) \rho_n (\omega) \nu (d \omega ) = \alpha \tag{2.52} \end{align} となる複素数$\alpha$が一意に存在する. |
このとき,$F$の $\omega_0 (\in \Omega )$ での値を $\alpha$ で定める. すなわち, $F(\omega_0 )$ $=$ $\alpha$ とする.
2.4.4 "観測量 (=測定器)"の定義
$X$を集合(普通は,局所コンパクト空間を想定するが,コンパクト化して,コンパクト空間と仮定しても,特に一般性を損ねることはない)とする. ${\cal F}( \subseteq 2^X (={\mathcal P}(X)=\{ \Xi \;|\; \Xi \subseteq X\}))$ (または, 2つ組$(X, {\mathcal F})$) は次の条件(a)-(c)を満たすとき 集合環 という.
\begin{align} & ({\rm a}): \emptyset (\mbox{="empty set"})\in {\cal F}, \quad \\ & ({\rm b}): \Xi_i \in {\cal F} \quad (i=1,2,\ldots) \Longrightarrow { \bigcup\limits_{i=1}^n } \;\; \Xi_i \in {\cal F} ,\quad { \bigcap\limits_{i=1}^n } \;\; \Xi_i \in {\cal F} \\ & ({\rm c}): \Xi_1 , \Xi_2 \in {\cal F} \Longrightarrow \Xi_1 \setminus \Xi_2 \in {\cal F} \quad (\mbox{ where, } \Xi_1 \setminus \Xi_2= \{ x \;| \; x \in \Xi_1 , x \notin \Xi_2 \}) \end{align}さらに条件$X \in {\mathcal F}$を満たすとき,集合環${\mathcal F}$(または, 対$(X, {\mathcal F})$)を 集合体 とよぶ. また,
| (d): | さらに,(b)で, 「$n=\infty$」とできるとき, 集合体${\mathcal F}$ (または, 対$(X, {\mathcal F})$)を $\sigma$-集合体 とよぶ. |
以下で、二つ((G$_1$)と(G$_2$))あって面倒であるが、${\mathcal A}$が有限次元の場合は (G$_1$)=(G$_2$)である。 無限次元の場合は、(G$_2$)の方が使い出がある。
(G$_1$):$C^*$- 観測量: 3つ組${\mathsf{O}} {=} (X, {\cal F}, F)$ は,次の条件(i)と(ii)を満たすとき, ${\mathcal A}$ 内の $C^*$-観測量(=測定器) と呼ばれる:| $\mbox{(i):}$ | $(X, {\mathcal F})$を 集合環 とする. | ||||||
| $\mbox{(ii):}$ | 写像$F: {\cal F} \to {\mathcal A}$
は次を満たす.
|
(G$_2$):$W^*$- 観測量: 3つ組${\mathsf{O}} {=} (X, {\cal F}, F)$ は,次の条件(i)と(ii)を満たすとき, $\overline{\mathcal A}$ 内の $W^*$-観測量(=測定器) と呼ばれる:
| $\mbox{(i):}$ | $(X, {\mathcal F})$は$\sigma$-集合体. | ||||||
| $\mbox{(ii):}$ | 写像$F: {\cal F} \to \overline{\mathcal A}$
は次を満たす.
|
また, $X$を 測定値空間 ,その元 $x (\in X)$を 測定値 と呼ぶ. また,
\begin{align} F(\Xi)^2 = F(\Xi) \qquad (\forall \Xi \in {\mathcal F} \end{align} のとき,${\mathsf{O}} {=} (X, {\cal F}, F)$を 射影観測量 と呼ぶ.定義2.18 $\rho \in {\frak S}^m({\mathcal A}^*) $で、 $(X, {\mathcal F}, F )$ は$W^*$-観測量 (in $\overline{\mathcal A}$)とする. ${\mathcal F}_\rho = \{ \Xi \in {\mathcal F} \;|\;$ $F(\Xi)$は $\rho$ で 本質的連続$\}$とする。 確率空間 $(X, {\mathcal F}, P_\rho )$が次を満たすとき、 サンプル確率空間 と言う:
| $(\sharp_1):$ | "${\mathcal F}_\rho$を含む最小の$\sigma$-集合体"= ${\mathcal F} $ |
| $(\sharp_2):$ | \begin{align} _{\stackrel{}{{\mathcal A}^* }}\Big(\rho, F(\Xi) \Big)_{\stackrel{}{\overline{\mathcal A} }} = P_\rho (\Xi ) \qquad (\forall \Xi \in {\mathcal F}_\rho ) \end{align} |
$C^*$-観測量に関しては、サンプル確率空間の存在は自明。。 したがって、$W^*$-観測量に関して、以下に述べる。 注意2.15で述べたように、 量子系 (すなわち、 ${\mathcal A}^*= {\mathcal Tr}(H)=\overline{\mathcal A}_*$ )の場合は明らかにサンプル確率空間は存在する。 しかしながら、古典系の場合は、自明とは言えないが、 重要な$W^*$-観測量は、サンプル確率空間を持つと考えてもよい。 したがって、本書全体を通して、 以下の仮定をする。