本節では,観測量の例を幾つか述べる.
例2.20-例2.23は,$C^*$-観測量かつ$W^*$-観測量であるが,
$W^*$-観測量として,説明する.
とは言っても、
当面の間は、
$C^*$と$W^*$の違いに神経質になる必要はない。
例 2.20 [存在観測量]
次の基本構造を考えよう:
\begin{align}
[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]
\end{align}
$X$を任意の集合(せいぜい,局所コンパクト空間を想定するが,コンパクト化して,コンパクト空間と仮定しても,特に一般性を損ねることはない)とする.
$\overline{\mathcal A}$
内の(射影)観測量${\mathsf O}^{\scriptsize \mbox{存}} =(X , \{\emptyset , X\} , F^{\scriptsize \mbox{ 存}})$
を次のように定める:
\begin{align}
F^{\scriptsize \mbox{ 存}}(\emptyset )=0 ,
\quad
F^{\scriptsize \mbox{ 存}}(X)=I
\tag{2.56}
\end{align}
この${\mathsf O}^{\scriptsize \mbox{ 存}} = (X , \{\emptyset , X\} , F^{\scriptsize \mbox{ 存}})$を
存在観測量
と呼ぶ.
さて,$\overline{\mathcal A}$内の
任意の観測量
${\mathsf O} =(X , {\cal F} , F)$
を考えよう.
観測量の定義から,
$\{ \emptyset , X \}$
$\subseteq$
${\cal F}$
(しかも,
$\{ \emptyset , X \}$
は
${\cal F}$
の部分$\sigma -$集合体
)
で,しかも,
となる.
したがって,
$(X , \{\emptyset , X\} , F^{\scriptsize \mbox{ 存}})$
$=$
$(X , \{\emptyset , X\} , F)$
となり,

| $\fbox{注釈2.3}$ |
上は、
バークリー(1685-1753)の
ボーア等によるコペンハーゲン解釈の主張は、「量子力学には測定者が不可欠」なのだから、 アインシュタインならずとも 「量子力学は物理学でない」 と言いたくなるだろう。 |
例 2.21 [単位$I$の分解 ; 言葉の仕切り]
$[C_0(\Omega ) \subseteq L^\infty (\Omega, \nu ) \subseteq B(L^2 (\Omega, \nu ))]$を古典系の基本構造とする. 関数族 $\{ f_x \}_{x\in X}$ が,状態空間$\Omega (\approx {\frak S}^p(C_0(\Omega)^*))$上の 単位の分解 であるとは,次を満たすときを言う:
| (i): | $F(\{ x_k \}) \ge 0$ for all $k=1,2,...$ |
| (ii): | $\sum_{k=1}^{\infty} [F(\{ x_k \})](\omega ) = 1$ $\quad (\forall \omega \in \Omega )$, |
$L^\infty(\Omega, \nu )
$内の観測量
${\mathsf O} =( X(=\{x_1,x_2, \cdots \}) , {\mathcal F}(=2^X), F )$
において,
任意の$x$
$(\in X)$
に対して,関数$f_{x}$
$(\in L^\infty (\Omega ) )$
を,
\begin{align}
f_x (\omega )= [F(\{x\})](\omega)
\qquad
(\forall \omega \in \Omega )
\end{align}
と定めれば,
関数族$\{ f_x \}_{x\in X}$
は,$\Omega$上の
単位の分解
となる.
このとき,関数族$\{ f_x \}_{x\in X}$
を観測量${\mathsf O} =( X , 2^X, F )$
の
単位の分解表現
(
または,
言葉の仕切り表現)
と呼ぶ.
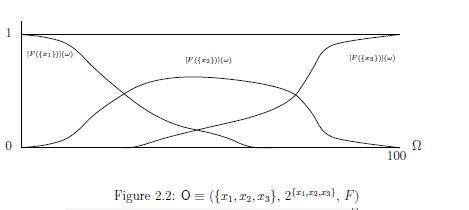
図2.2で, $\Omega=閉区間[0,100] ( \subset {\mathbb R})$ を温度の軸, $X=\{ 冷,温,熱 \}$ として, $f_{x_1}=f_{冷}$, $f_{x_2}=f_{温}$, $f_{x_3}=f_{熱}$ と見れば, 単位の分解 $\{f_{x_1}, f_{x_2}, f_{x_3} \}$ は,「冷,温,熱」の3つの言葉の仕切りであることが わかると思う.
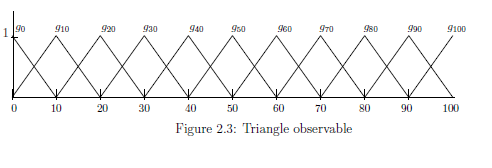
例 2.22 [約-観測量]$[C_0(\Omega ) \subseteq L^\infty (\Omega, \nu ) \subseteq B(L^2 (\Omega, \nu ))]$を古典系の基本構造とする. たとえば, 状態空間を閉区間$\Omega = [0,100]$ $( \subseteq {\mathbb R})$ で定める. 各 $n \in {\mathbb N}_{10}^{100} = \{0,10,20,\ldots,100\}$ に対して, (三角型)連続関数 $g_{n}:\Omega \to [0,1]$ を次のように定める(図2.3):
\begin{align} g_{n} (\omega) = \left\{\begin{array}{ll} 0 & \quad (0 {{\; \leqq \;}}\omega {{\; \leqq \;}}n-10 ) \\ {\displaystyle \frac{\omega - n -10}{10} } & \quad (n-10 {{\; \leqq \;}}\omega {{\; \leqq \;}}n ) \\ {\displaystyle - \frac{\omega - n + 10}{10} } & \quad (n {{\; \leqq \;}}\omega {{\; \leqq \;}}n+10 ) \\ 0 & \quad (n+10 {{\; \leqq \;}}\omega {{\; \leqq \;}}100 ) \end{array}\right. \tag{2.57} \end{align}当然, 関数族$\{g_{0}, g_{10}, g_{20},\ldots, g_{100} \}$ は, 閉区間 $[0,100]$ 上の単位の分解となる.
ここで, 測定値空間$Y$ を $Y={\mathbb N}_{10}^{100}$ として, ${\mathsf O}_{約}= (Y , 2^Y, G_{約} )$ を次 のように定める:
\begin{align} & [G_{約}(\emptyset )](\omega ) = 0, \qquad [G_{約}(Y )](\omega ) = 1 \\ %[F(\emptyset )](\omega ) = 0, %\quad & [G_{約} (\Gamma )](\omega ) = \sum\limits_{n \in \Gamma } g_n (\omega ) \quad (\forall \Gamma \in 2^{{\mathbb N}_{10}^{100} }) %%P%\TAG{3.5} \end{align}このとき, ${\mathsf O}_{約}= (Y (= {{\mathbb N}_{10}^{100} } ) , 2^Y, G_{約} )$ を,$C([0,100])$内の 約-観測量 と呼ぶ.
例 2.23 [正規観測量 ( or, ガウス観測量 )]

$[C_0(\Omega ) \subseteq L^\infty (\Omega, \nu ) \subseteq B(L^2 (\Omega, \nu ))]$を古典系の基本構造とする.ここで, $\Omega = {\mathbb R}(=\mbox{実直線})$ または, $\Omega = 区間[a, b] $ $\;(\subseteq {\mathbb R} )$ として,ルベーグ測度$\nu (d\omega) (= d \omega )$を仮定する. また,$\sigma>0$を 標準偏差とする. $L^\infty (\Omega,\nu)$内の 正規観測量 ${\mathsf O}_{G_\sigma} {{=}} ({\mathbb R}, {\cal B}_{\mathbb R}, G_{\sigma})$ を次のように定義する:
\begin{align} [G_{\sigma}(\Xi)] (\omega) = \frac{1}{\sqrt{2 \pi \sigma^2}} \int_{\Xi} e^{- \frac{(x - \omega)^2}{2 \sigma^2}} dx \quad (\forall \Xi \in {\cal B}_{\mathbb R}(\mbox{ボレル集合体}), \forall \omega \in \Omega (={\mathbb R} \mbox{ or } [a,b] )) \end{align} これは,統計学におけるもっとも基本的な観測量である.次の例2.24と例2.25は,$W^*$-観測量であるが, $C^*$-観測量ではない. 特に,精密観測量という基本的な観測量が $C^*$-観測量ではないことは,$C^*$-代数アプローチの限界であるといえる.
例 2.24 [精密観測量]
$[C_0(\Omega ) \subseteq L^\infty (\Omega, \nu ) \subseteq B(L^2 (\Omega, \nu ))]$を古典系の基本構造とする. ${\mathcal B}_\Omega$をボレル$\sigma$-集合体とする. このとき, $ L^\infty (\Omega, \nu ) $内の (射影)観測量 ${\mathsf O}^{(e)} = (\Omega , {\mathcal B}_\Omega, F^{(exa)})$を 次のように定める: 定義関数$\chi$を使って書くと,
\begin{align} [F^{(exa)})(\Xi)](\omega) = \chi_{_\Xi} (\omega) = \left\{\begin{array}{ll} 1 & ( \omega \in \Xi) \\ \\ 0 & ( \omega \notin \Xi ) \quad \end{array}\right. \tag{2.58} \end{align}${\mathsf O}^{(exa)} = (\Omega , {\mathcal B}_\Omega, F^{(exa)})$を 精密観測量 と言う。
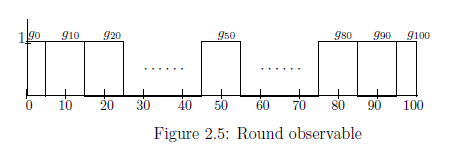
例 2.25 [四捨五入観測量(=まるめ観測量)] $[C_0(\Omega ) \subseteq L^\infty (\Omega, \nu ) \subseteq B(L^2 (\Omega, \nu ))]$を古典系の基本構造とする. 状態空間$\Omega(\approx {\frak S}^p(C_0(\Omega)^*))=\Omega $を,閉区間$ [0,100]$ としてルベーグ測度$d \omega$を仮定する. 各 $n \in {\mathbb N}_{10}^{100} $ $ {{=}} \{0,10,20,\ldots,100\}$ に対して, 関数 $g_{n}:\Omega \to [0,1]$ を次のように定める:
\begin{align} g_{n} (\omega) = \left\{\begin{array}{ll} 0 & \quad (0 {{\; \leqq \;}}\omega {{\; \leqq \;}}n-5 ) \\ 1 & \quad (n-5 {{\; < \;}}\omega {{\; \leqq \;}}n +5) \\ 0 & \quad (n+5 {{\; < \;}}\omega {{\; \leqq \;}}100 ) \end{array}\right. \end{align}観測量 ${\mathsf O}_{{RND}}= (Y ({{=}} {\mathbb N}_{10}^{100}) , 2^Y, G_{{RND}})$ in $L^\infty (\Omega , \nu )$は次を満たすとき、四捨五入観測量と言う:
\begin{align} & [G_{{RND}}(\emptyset )](\omega ) = 0, \quad [G_{{RND}}(Y )](\omega ) = 1 \\ & [G_{{RND}} (\Gamma )](\omega ) = \sum\limits_{n \in \Gamma } g_n (\omega ) \quad (\forall \Gamma \in 2^Y = 2^{{\mathbb N}_{10}^{100} }) \end{align}