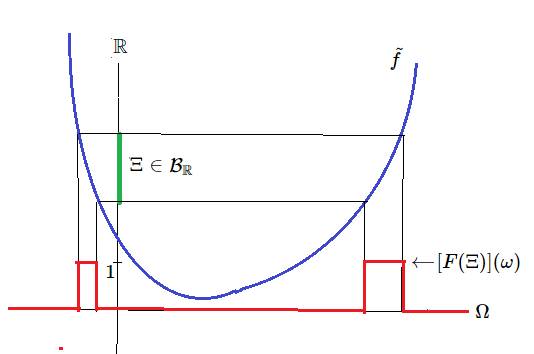
例 2.26 [システム量] $[C_0(\Omega ) \subseteq L^\infty (\Omega, \nu ) \subseteq B(L^2 (\Omega, \nu ))]$を古典系の基本構造とする. 実数値連続関数 ${\widetilde f}: \Omega \to {\mathbb R}$ ( 一般には， 実数値可測関数${\widetilde f}: \Omega \to {\mathbb R}^n$ でよい ) を，$\Omega$上の システム量 と呼ぶ． 基本代数 ${L^\infty ( \Omega, \nu )}$ 内の 射影観測量 ${\mathsf O}=({\mathbb R}, {\cal B}_{\mathbb R} , F)$ を次のように定義する： \begin{align*} [F(\Xi)] (\omega) = \left\{ \begin{array}{l} 1 \quad \omega \in {\widetilde f}^{-1}(\Xi) \; \mbox{のとき}\\ \\ 0 \quad \omega \notin {\widetilde f}^{-1}(\Xi) \; \mbox{のとき} \end{array} \right. \qquad ( \forall \Xi \in {\cal B}_{\mathbb R} %, % ) \end{align*} ここで， \begin{align} {\widetilde f} (\omega) = \lim_{N \to \infty } \sum\limits_{n=-N^2}^{N^2} \frac{n}{N} \left[F \bigm( [\frac{n}{N},\frac{n+1}{N} ) \bigm) \right](\omega) = \int_{\mathbb R} \lambda [F(d \lambda) ](\omega) \qquad \tag{2.59} \end{align} であることに注意して， 次の同一視: \begin{align} {{{\widetilde f}} \atop {\scriptsize \mbox{ ($\Omega$上のシステム量)}} } {{\longleftrightarrow}\atop{}} {{{\mathsf O}=({\mathbb R}, {\cal B}_{\mathbb R} , F)} \atop {\scriptsize \mbox{ ($L^\infty(\Omega,\nu)$内の射影観測量)}} } \tag{2.60} \end{align} を得る．この${\mathsf O}$ をシステム量${\widetilde f}$ の 観測量表示 と呼ぶ． したがって，

例 2.27 [位置観測量，運動量観測量，エネルギー観測量]基本代数 $L^\infty (\Omega, \nu)$ 内で， ニュートン力学を考える． 簡単のために， 2次元空間を考えて， \begin{align*} \Omega = {\mathbb R}_q\times{\mathbb R}_p {{=}} \{ (q,p)=(位置, 運動量) \; | \; q,p\in{\mathbb R}\} \end{align*} とする。 次の物理量は基本的である． \begin{align*} & {\widetilde q}:\Omega \to {\mathbb R}, \quad &{\widetilde q} (q,p)=&q \quad (\forall (q,p) \in \Omega ) \\ & {\widetilde p}:\Omega \to {\mathbb R}, \quad &{\widetilde p}(q,p)=&p \quad (\forall (q,p) \in \Omega ) \\ & {\widetilde e}:\Omega \to {\mathbb R}, \quad & {\widetilde e} (q,p)=& { \mbox{[ポテンシャルエネルギー]}+ \mbox{[運動エネルギー]} } \\ & &\quad =& \underset{(ハミルトニアン{\cal H}の簡単な場合)}{U(q)+ \frac{p^2}{2m} } \qquad (\forall (q,p) \in \Omega ) \end{align*} ここに，$m$は粒子の質量 とする． これらの物理量は， (2.60) の対応の下に， それぞれ 位置{観測量，運動量観測量， エネルギー観測量 とも呼ばれる．
例　2.28[エルミート行列は射影観測量] 基本構造$[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]$ を有限量子系の基本構造 $$ [B({\mathbb C}^n )) \subseteq B({\mathbb C}^n )) \subseteq B({\mathbb C}^n ))] $$

とする. エルミート行列$A (\in B({\mathbb C}^n ))$ は射影観測量と見なすことができることを示そう( 簡単のため，$n=3$の場合で書く)． エルミート行列の対角化定理により，

と表現できる． ここに，$U$ $(\in B({\mathbb C}^3))$はユニタリ行列 (すなわち， $U^* U=U U^*=I=単位行列$)， $x_k \in {\mathbb R} $は エルミート行列 $A$の固有値 である． ここで， $X=\{ x_1, x_2, x_3 \}$ として，

として， $B({\mathbb C}^3)$内の 射影観測量${\mathsf O}_A =({\mathbb R },{\mathcal B}_{\mathbb R}, F_A)$ を定めることができる． また， 逆に， 射影観測量${\mathsf O}_A =({\mathbb R },{\mathcal B}_{\mathbb R}, F_A) $ から始めても， エルミート行列$A$ $(=\sum\limits_{i=1}^3 x_i F_A(\{x_i\}) \;)$を 構成できる． このようにして， エルミート行列$A$ を 射影観測量${\mathsf O}_A $ とを同一視， すなわち， 次の同一視: \begin{align} \underset {\scriptsize \mbox{ (エルミート行列)}}{{A}} \longleftrightarrow \underset{\scriptsize \mbox{ (射影観測量)}} {{\mathsf O}_A =({\mathbb R },{\mathcal B}_{\mathbb R}, F_A) } \tag{2.62} \end{align} を得る

$A (\in B({\mathbb C}^n) )$ をエルミート行列とする。 \begin{align*} \rho= |\omega \rangle \langle \omega |, \quad \omega = \left[\begin{array}{l} \omega_1 \\ \omega_2 \\ \vdots \\ \omega_n \end{array}\right] \in {\mathbb C}^n, \|\omega\|=1 \end{align*} として、 量子測定 ${\mathsf M}_{B({\mathbb C}^n)}({\mathsf O}_A,$ $S_{[\rho]})$ を考えよう。 ボルンの量子測定理論 (または, その言語化である「 言語ルール 1 ($\S$2.7)」 ) によれば、 次が言える：

(ここで、トレース"${\mbox{Tr}}$", 定義2.9を見よ). したがって、 測定値の 期待値 は次で与えられる：

また、 分散 $(\delta_A^\omega)^2$ は次で与えられる：

例 2.29 [スペクトル分解]

$H$をヒルベルト空間とする.. 量子系の基本構造を考えよう

射影観測量 ${\mathsf O}=({\mathbb R}, {\mathcal B}_{\mathbb R}, F)$を スペクトル分解 と呼ぶ. スペクトル分解定理の主張は,次の同値性((a)$\Leftrightarrow$(b))である.

の下に,自己共役作用素は射影観測量と見なせる. この 同一視(2.66)は, 古典版の 同一視 (2.60)の量子版 であることを再確認せよ．
上の議論は,以下のように一般化できる.次の同値性((c)$\Leftrightarrow$(d))が成立する.