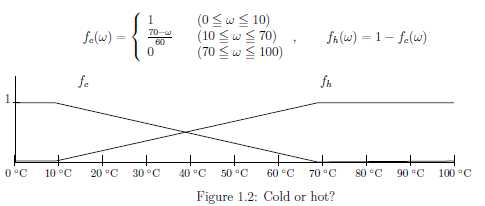
測定理論は次のように定式化される.
すなわち,
\[
\underset{\mbox{ (=量子言語)}}{\fbox{純粋測定理論 (A)}}
:=
\underbrace{
\underset{\mbox{ (\(\S\)2.7)}}{
\overset{
[\mbox{ (純粋) 言語ルール1}]
}{\fbox{純粋測定}}
}
\quad + \quad
\underset{\mbox{ ( \(\S \)10.3)}}{
\overset{
[{\mbox{ 言語ルール2}}]
}{\fbox{因果関係}}
}
}_{\mbox{ 一種の呪文 (アプリオリな総合判断)}}
+
\underbrace{
\underset{\mbox{
(\(\S\)3.1)
}}
{
\overset{
{}}{\fbox{言語的解釈}}
}
}_{\mbox{ 呪文の使い方のマニュアル}}
\]
となる.
以下に,測定に関する言語ルール1(測定)
を説明する.なお,因果関係に関する言語ルール2は第10章
で述べる.
2.7.1 言語ルール1(測定)
いかなる
システム(=測定対象)
$S$も,
ある基本構造
$[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]$
内で定式化される.
システム$S$の
状態
(正確には,
純粋状態
)
は,
状態空間
${\frak S}^p({\mathcal A}^*)$内の元
$\rho$
で表現される.
観測量
(または,
測定器
と言った方がわかりやすいかもしれない)
は
${\mathcal A}$
内の$C^*$-観測量
${\mathsf O}$
${{=}}$
$(X , {\cal F} , F)$
$\Big($
または,
$\overline{\mathcal A}$
内の$W^*$-観測量
${\mathsf O}$
${{=}}$
$(X , {\cal F} , F)$
$\Big)$
で表現される.
また,
| $(A_1):$ | 測定者が,
状態
$\rho$
をもつ
測定対象
に対して,
$
\left[\begin{array}{ll}
\mbox観測量
[{\mathsf O}]
を
\\
\mbox{測定器}
[{\mathsf O}]
で
\end{array}\right]
$
測定
する
|
を
略して,
| $(A_1):$ |
$W^*$-測定
${\mathsf M}_{\overline{\mathcal A}} \big({\mathsf O} , S_{[\rho]} \big)$
$\Big($
または,
$C^*$-測定
${\mathsf M}_{{\mathcal A}} \big({\mathsf O} , S_{[\rho]} \big)$
$\Big)$
|
と言う.
また,
$W^*$-測定
${\mathsf M}_{\overline{\mathcal A}} \big({\mathsf O} , S_{[\rho]} \big)$
$\Big($
または,
$C^*$-測定
${\mathsf M}_{{\mathcal A}} \big({\mathsf O} , S_{[\rho]} \big)$
$\Big)$
により
測定値
$x$
$(\in X)$
を得る.
基本構造 $[ {\mathcal A} \subseteq \overline{\mathcal A} \subseteq {B(H)}]$内の
$W^*$-測定 ${\mathsf M}_{\overline{\mathcal A}} \big({\mathsf O}{{=}} (X, {\cal F} , F), S_{[\rho] } \big)$ $\Big($ or, $C^*$-測定 ${\mathsf M}_{{\mathcal A}} \big({\mathsf O}{{=}} (X, {\cal F} , F), S_{[\rho] } \big)$ $\Big)$を考える.
準備2.30二つの「測定($W^*$-測定と$C^*$-測定)」があって,混乱しがちなので,念の為に確認すると,
| $\bullet$ |
-
$W^*$-測定 ${\mathsf M}_{\overline{\mathcal A}} \bigl({\mathsf O}{{=}} (X, {\cal F} , F) , S_{[\rho] } $
と
$C^*$-測定 ${\mathsf M}_{{\mathcal A}} \big({\mathsf O}{{=}} (X, {\cal F} , F), S_{[\rho] } \big)$
|
において、
| $(A_2):$ |
$\left\{\begin{array}{ll}
\mbox{ $W^*$-測定
${\mathsf M}_{\overline{\mathcal A}} \big({\mathsf O} , S_{[\rho]} \big)$}
&\cdots
\mbox{
${\mathsf O}$ は $W^*$- 観測量 ,$\rho \in {\frak S}^p ({\mathcal A}^* )$
}
\\
\mbox{ $C^*$-測定
${\mathsf M}_{{\mathcal A}} \big({\mathsf O} , S_{[\rho]} \big)$}
&\cdots
\mbox{
${\mathsf O}$ は $C^*$- 観測量 ,$\rho \in {\frak S}^p ({\mathcal A}^* )$
}
\end{array}\right.
$
|
本書では,主に
$W^*$-測定
に集中する.
次の言語ルール1は,
「ボルンの量子力学の確率解釈」
(
Born, M.
Z. Phys. (37) pp.863--867 (1926))
の言語化(=ことわざ化)である.
\begin{align}
\overset{\mbox{ (ボルンの発見した物理法則)}}{
\underset{\mbox{ (物理学)}}{
{\fbox{量子力学 (ボルンの量子測定)}}
}
}
\xrightarrow[\mbox{言語化(ことわざ化)}]{}
\overset{\mbox{ (一種の呪文)}}{
\underset{\mbox{ (形而上学, 言語)}}{
{\fbox{測定理論(言語ルール1)}}
}
}
\end{align}
-
ことわざ化すると、適用範囲が飛躍的に拡大する:たとえば、

$\Large{\mbox{猿が}}
\left\{\begin{array}{ll}
\Large{\mbox{弘法大師}}
\\
\small{\mbox{(弘法も筆の誤り)}}
\\
\\
\Large{\mbox{河童}}
\\
\small{\mbox{(河童の川流れ)}}
\\
\\
\cdots
\end{array}\right\}
\mbox{にもなる}
$
 言語ルール1(測定) 純粋系${\mathsf M}_{\overline{\mathcal A}} \big({\mathsf O}{},
S_{[\rho] }\big)$
言語ルール1(測定) 純粋系${\mathsf M}_{\overline{\mathcal A}} \big({\mathsf O}{},
S_{[\rho] }\big)$
-
($B_1$):言語ルール1(測定) 純粋型 (この2.7節までの準備で読めるはず)
あらゆるシステムはある基本構造
$[ {\mathcal A} \subseteq \overline{\mathcal A}]_{B(H)}$内で定式化できる.
$[ {\mathcal A} \subseteq \overline{\mathcal A}]_{B(H)}$
内で定式化された$W^*$-測定
${\mathsf M}_{\overline{\mathcal A}} \big({\mathsf O}{{=}} (X, {\cal F} , F),
S_{[\rho] } \big)$
$\Big($
または,
$C^*$-測定}
${\mathsf M}_{{\mathcal A}} \big({\mathsf O}{{=}} (X, {\cal F} , F),
S_{[\rho] } \big)$
$\Big)$
を
考えよう.
このとき,
$W^*$-測定
${\mathsf M}_{\overline{\mathcal A}} \bigl({\mathsf O} , S_{[\rho] } \bigl)$
$\Big($
または,
$C^*$-測定
${\mathsf M}_{{\mathcal A}} \big({\mathsf O}{{=}} (X, {\cal F} , F),
S_{[\rho] } \big)$
$\Big)$
により得られる
測定値$ x$
$(\in X )$
が,
$ \Xi $
$(\in {\cal F})$
に属する
確率
は,
(もし$F(\Xi)$が$\rho$で本質的連続ならば)
$\rho( F(\Xi))$
$(\equiv _{{{\mathcal A}^*}}(\rho, F(\Xi) )_{\overline{\mathcal A}} )$
で与えられる

| $\fbox{注釈2.4}$ |
上記の言語ルール 1 の源流は ボルン(1926)による.
"確率”に関しては、いろいろな意見があるかもしれない。たとえば、アインシュタインはボルンに以下のような手紙を送っている (1926):
| (A2): |
量子力学にはとても尊敬の念を抱いています。しかし内なる声が私に、その理論はまだ完璧ではないと言っています。量子力学はとても有益なものではありますが、神の秘密にはほとんど迫っていません。少なくとも私には、
神はサイコロを振らない
という確信があるのです
|
量子言語の立場からは、ボルンもアインシュタインも正しいのだと思う。結局、
言語的科学観(「言葉が先,世界が後」の精神)は, 実在的科学観(「世界が先,言葉が後」の精神)
\begin{align*}
\overset{\mbox{(「世界が先,言葉が後」の精神) }}{
\underset{\mbox{(アインシュタイン)}}{\fbox{$\mbox{実在的科学観}$}}}
\quad
\underset{\mbox{v.s.}}{\longleftrightarrow}
\quad
\overset{\mbox{(「言語が先,世界が後」の精神) }}{
\underset{\mbox{(ボーア、ボルン)}}{\fbox{$\mbox{言語的科学観}$}}}
\end{align*}
と思えばよいからである。言語的科学観ならば、「神の秘密」に迫る必要はなくて、
確率は形而上学的概念なのだから、
からである。
ボーア=アインシュタイン論争は、20世紀の科学の華である。 結局、「敗者はアインシュタイン」という印象だけが残ってしまったが、
アインシュタインが負けたのは、「量子言語の言語的科学観による量子力学」であると考える。
アインシュタインが勝負したかったはずの
「実在的科学観による量子力学」は未完であって、まだ決着が付いたわけではない。
それにしても、
ことを当然のように直感したアインシュタインは、どこまで天才なのだろうか?
フォン・ノイマンやコルモゴロフには、このような泥臭い議論をスルーする器用さがあったが、
アインシュタインのこだわりは徹底している。
|
サプリ
さて、「アインシュタインは量子力学の何が気に入らなかったのか?」であるが、常識的には、
| $\bullet$ |
非局所性(=遠隔作用=超光速)
|
であるが、本書的には
| $\bullet$ |
測定(とか、確率)が形而上学的概念であること
|
となる。
量子力学は、[測定]+[因果関係]の形をもつが、 すなわち、[測定(言語的;人為的)]+[因果関係(実在的;物理的)]となって、不自然な接続となる。
量子力学の解釈問題とは、
-
「測定(人為的)と因果関係(物理的)」を如何に滑らかに接続させるか?
とみることもできる。 この文脈では、二つの方法があって、
(a) 「測定(物理的)と因果関係(物理的)」と見る方法
(b)「測定(人為的)と因果関係(人為的)」と見る方法
である。
大抵の提案は(a)であるが、
量子言語は(b)の方法である。
2.7.2:簡単な例
次の例は,例1.2とまったく同じものを,
言語ルール1
の下に
書いたに過ぎない.
例 2.31[コップの水の冷・熱の測定(例1.2の続き)]
古典系の基本構造:
\begin{align}
\mbox{
$[C_0(\Omega ) \subseteq L^\infty (\Omega, \nu ) \subseteq B(L^2 (\Omega, \nu ))]$
}
\end{align}

を考えよう.ここで,
$\Omega=閉区間[0,100](\subset {\mathbb R})$として,
可換$C^:$代数${\mathcal A}=C_0(\Omega)$と
可換$W^:$代数$\overline{\mathcal A}=L^\infty (\Omega, \nu)$
を考える.
状態空間
${\frak S}^p(C_0(\Omega)^*)$
は
\begin{align}
{\frak S}^p(C_0(\Omega)^*)=\{ \delta_\omega \in {\mathcal M}(\Omega)
\;|\;
\omega \in \Omega \} \approx \Omega =[0,100]
\end{align}
となる.
測定値空間$X=\{冷, 熱\}$として,
冷熱-測定器
${\mathsf O}_{ch}= (X , 2^X, F_{ch} )$ in $L^\infty ( \Omega )$
を以下のように定義する.
\begin{align}
&
[F_{ch}(\emptyset )](\omega ) = 0,
\quad
&&
[F_{ch}(X )](\omega ) = 1
\\
&
[F_{ch}(\{c\})](\omega ) = f_{c} (\omega ),
&&
[F_{ch}(\{h\})](\omega ) = f_{h} (\omega )
\end{align}
よって、t測定${\mathsf M}_{L^\infty ( \Omega )} ( {\mathsf O}_{ch}, S_{[\delta_\omega]} )$ $($ 略して,
${\mathsf M}_{L^\infty ( \Omega )} ( {\mathsf O}_{ch}, S_{[{\omega}]} )$を得る.
したがって, たとえば,
$\omega=55$°Cとおいて、言語ルール1 ($\S$2.7)の言葉遣いで、
次の翻訳を得る。
| (a): | 測定$\left.\begin{array}{ll}{\mathsf M}_{L^\infty ( \Omega )} ( {\mathsf O}_{ch}, S_{[ \omega(=55)]} )
\end{array}\right.$によって得られる測定値 $x(\in X {{=}} \{c, h\})$
が
$
\left[\begin{array}{ll}
\emptyset
\\
\{ \mbox{c}\}
\\
\{ {h} \}
\\
\{ {c} ,{h}\}
\end{array}\right]
$
に属する確率は、
$
\left[\begin{array}{ll}
[F_{ch}( \emptyset )](55)= 0
\\
[F_{ch}(
\{
{ c}
\}
)](55)=
0.25
\\
[F_{ch}(
\{
{ h}
\}
)](55)=
0.75
\\
[F_{ch}(
\{
{ c}
,
{ h}
\}
)](55)=
1
\end{array}\right]
$
である。
|


 言語ルール1(測定) 純粋系${\mathsf M}_{\overline{\mathcal A}} \big({\mathsf O}{},
S_{[\rho] }\big)$
言語ルール1(測定) 純粋系${\mathsf M}_{\overline{\mathcal A}} \big({\mathsf O}{},
S_{[\rho] }\big)$