2.8.1: 言語的科学観─人間の言語能力の驚異
物理学(実在的記述法)の適用範囲はかなり明確であるが,
測定理論(言語的記述法)の適用範囲は漠然としている.
ことわざの「猿も木から落ちる」の
適用範囲が明確でないのと同じである.
実在的科学観に刷り込まれた感覚からは,
本節で述べる例に違和感を持って当然と思う.
頼りにできるのは,(実験検証できない)
言語ルール1だけで,
我々のできることは,
| (a): | $ \left\{\begin{array}{ll}
\mbox{(a$_1$): 言語ルール1の言葉遣いに,完全に忠実であること( $\S$2.7)
}
\\
\\
\mbox{(a$_2$):
人間の言語能力を信じること
}
\end{array}\right.
$
|
だけである.
こう言うと,
| (b): |
$\qquad
\qquad$ これで科学になるのか?
|
と思うかもしれない。
しかし,
言語的科学観(「言葉が先,世界が後」の精神)は,
実在的科学観(「世界が先,言葉が後」の精神)
とは,
まったく異なる原理から成り立つ科学観である.
これに
留意して,以下の例を読んでもらいたい。
2.8.2基本的な例─壷問題等
測定理論は
言語なので,
多くの例を演習・訓練しなければ,上達しない.
言語ルール1(測定)の言葉遣いで表現できるような現象の例
をいくつか述べる.
もちろん,どれも
中高生レベルを超えるものではない.シュテルン=ゲルラッハの実験の例も,数学的には,「高校の数学2」レベルである.
例 2.32[コップの水の温度の近似測定
(例2.2
[約-観測量]の続き)]約-観測量)]
古典系の基本構造:
\begin{align}
\mbox{
$[C_0(\Omega ) \subseteq L^\infty (\Omega, \nu ) \subseteq B(L^2 (\Omega, \nu ))]$
}
\end{align}
を考えよう。
ここに、$\Omega =$"閉区間 $[0, 100]$"(ルベーグ測度 $\nu$を仮定する).

いろいろな温度$\omega$℃
$(0 {{\; \leqq \;}}\omega {{\; \leqq \;}}100)$
のコップの水(お湯)に,
多くの被験者(たとえば,1000人)に
飲んでもらって,「約何十℃ですか?」を
アンケート形式で質問する.
そして,得られた
データ(たとえば,$h_{n}(\omega)$人が,
約$n$℃
$(n=0,10,20,\ldots,90,100)$
と答えたとして,
これ
を正規化(かつ,折れ線化)して,以下の
$g_{n}(\omega)= h_{n}(\omega)/被験者数$
を得たとする.
すなわち,
各
$n \in {\mathbb N}_{10}^{100} {{=}} \{0,10,20,\ldots,100\}$
に対して,
関数
$g_{n}:\Omega \to [0,1]$
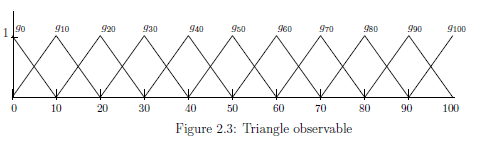
を次のように定める(
図2.2と同じで,
再び式を書くと
):
\begin{align}
g_{n} (\omega)
=
\left\{\begin{array}{ll}
0 & \quad (0 {{\; \leqq \;}}\omega {{\; \leqq \;}}n-10 ) \\
{\displaystyle \frac{\omega - n -10}{10} }
& \quad (n-10 {{\; \leqq \;}}\omega {{\; \leqq \;}}n ) \\
{\displaystyle
- \frac{\omega - n + 10}{10}
}
& \quad (n {{\; \leqq \;}}\omega {{\; \leqq \;}}n+10 ) \\
0 & \quad (n+10 {{\; \leqq \;}}\omega {{\; \leqq \;}}100 )
\end{array}\right.
\end{align}
| (a): | $1000$人の被験者の中から1人選んで,
$47$℃
のコップの水を飲んでもらって,
「約何十℃ですか?」と
質問したとき,その被験者が
$
\left[\begin{array}{ll}
\mbox{"about 40°C"}
\\
\mbox{"about 50°C"}
\end{array}\right]
$
と答える確率は、
$
\left[\begin{array}{ll}
g_{\text 40}(47)=0.25
\\
f_{\text 50}(47)=0.75
\end{array}\right]
$
である。
|
この日常言語の文言(a)を言語ルール1( $\S$2.7)
の言葉で表現しよう.
$Y={\mathbb N}_{10}^{100}$とする。
$
L^\infty([0,100], \nu )
$内の
約-観測量
${\mathsf O}_{約}= (Y({{=}} {\mathbb N}_{10}^{100}) , 2^Y, G_{約} )$
を次
のように定める:
\begin{align*}
&
[G_{約}(\emptyset )](\omega ) = 0,
\quad
\qquad
\qquad
[G_{約}(X )](\omega ) = 1
\\
&
[G_{約} (\Gamma )](\omega ) = \sum\limits_{n \in \Gamma } g_n (\omega )
\quad
\qquad
(\forall \Gamma \in 2^{{\mathbb N}_{10}^{100} })
\end{align*}
このとき,
${\mathsf O}_{約}= (Y( {{=}} {\mathbb N}_{10}^{100}) , 2^Y, G_{約} )$
は$L^\infty([0,100], \nu )$内の観測量で,
したがって,測定
${\mathsf M}_{L^\infty([0,100], \nu )} ( {\mathsf O}_{約},$
$ S_{[\omega]} )$
が定まる.
また,
任意の$\Gamma (\in 2^{{\mathbb N}^{100}_{10}})$に対して,$G_{約}(\Gamma )$
$(\in L^\infty ( [0, 100], \nu ) )$は
任意の状態$\omega_0 (\in [0, 100])$で(本質的に)連続である.
したがって,
測定
$
{\mathsf M}_{L^\infty([0,100], \nu )} ( {\mathsf O}_{約}, S_{[
\omega_0]} )
$の
$\omega_0$でのサンプル空間は,
$(Y({{=}} {\mathbb N}_{10}^{100}) , 2^Y,[ G_{約}(\cdot )](\omega_0 ) )$
となる.
たとえば,
$\omega=47℃$
として,次の測定理論による記述を得る:
| $(b):$ | 測定$
{\mathsf M}_{L^\infty ( \Omega )} ( {\mathsf O}_{約},$ $S_{[ \omega(=47)]} )$によって測定値
$
\left[\begin{array}{ll}
{\mbox{about 40°C}}
\\
\mbox{about 50°C}
\end{array}\right]
$が得られる確率は$
\left[\begin{array}{ll}
{[G_{約}( \{ 40 \})](47)=0.3}
\\
{[G_{約}( \{ 50 \})](47)=0.7}
\end{array}\right]
$
で与えられる。
|
したがって, 次の翻訳を得た:
\begin{align}
\underset{\mbox{ (日常言語)}}{\fbox{statement (a)}}
\xrightarrow[{\mbox{翻訳}}]{}
\underset{\mbox{ (量子言語)}}{\fbox{statement (b)}}
\tag{2.69}
\end{align}
例 2.33 [精密測定]さて、古典系の基本構造:
\begin{align}
\mbox{
$[C_0(\Omega ) \subseteq L^\infty (\Omega, \nu ) \subseteq B(L^2 (\Omega, \nu ))]$}
\end{align}
を考える.
${\mathcal B}_\Omega$をボレル$\sigma$-集合体とする.
このとき,
$
L^\infty (\Omega, \nu )
$内の
精密観測量
${\mathsf O}^{(e)} = (X(=\Omega) , {\mathcal F}(={\mathcal B}_\Omega), F^{\rm (exa)})$を
次のように定める:
\begin{align}
[F^{\rm (exa)}(\Xi)](\omega)
=
\chi_{_\Xi} (\omega) =
\left\{\begin{array}{ll}
1 \quad
& ( \omega \in \Xi )\\
\\
0 & ( \omega \notin \Xi
)
\end{array}\right.
\qquad
(\forall \Xi \in {\mathcal B}_\Omega)
\end{align}
状態$\delta_{\omega_0 } \approx \omega_0 (\in \Omega )$に対して,
精密測定
${\mathsf M}_{L^\infty ( \Omega, \nu )} (
{\mathsf O}^{\rm (exa)}, S_{[\delta_{\omega_0} ]})$
を考える.
| (a): | $\omega_0 \in D \subseteq \Omega$となる任意の開集合$D$を考える.
精密測定 ${\mathsf M}_{L^\infty ( \Omega, \nu )} ({\mathsf O}^{\rm (exa)}, S_{[\delta_{\omega_0 }]})$によって得られる測定値
が$D$に属する
確率は
\begin{align}
{_{C_0(\Omega)^*}}
\Big(
\delta_{{\omega_0}},
\chi_{_D}
\Big){_{L^\infty(\Omega, \nu )}}
=
1
\end{align}
である。
|
$D$の任意性から,
| $(b):$ |
精密測定 ${\mathsf M}_{L^\infty ( \Omega, \nu )}$ $ ( {\mathsf O}^{\rm (exa)},$ $ S_{[\delta_{\omega_0 }]})$によって,
確率1で, 測定値 $\omega_0$が得られる。
|
と結論できる。
また,
\begin{align}
{\mathcal F}_{\omega_0}=\{
\Xi \in {\mathcal F}
\;:\;
\omega_0 \notin \mbox{"closure of $\Xi$"$\setminus$ "the
interior of
$\Xi$"}
\}
\end{align}
とすれば,$\Xi \in {\mathcal F}_{\omega_0} $のとき,
$F(\Xi)$は$\omega_0$で連続で,しかも,
${\mathcal F}$は,${\mathcal F}_{\omega_0}$を含む最小の$\sigma$-集合体である.
したがって,
次を満たす確率空間$(X, {\mathcal F}, P_{\delta_{\omega_0}})$が存在する:
\begin{align}
P_{\delta_{\omega_0}}( \Xi )
=
[F(\Xi )](\omega_0 )
\qquad
(\forall \Xi \in {\mathcal F}_{\omega_0})
\end{align}
すなわち,
| $(c):$ | 精密測定
${\mathsf M}_{L^\infty ( \Omega, \nu )} (
{\mathsf O}^{(e)}, S_{[\delta_{\omega_0 }]})$
は
サンプル空間$(X, {\mathcal F}, P_{\delta_{\omega_0}})$を持つ
|
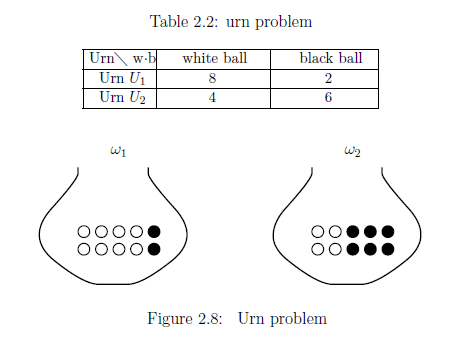
例 2.34 「壺問題]2つの壷 ${U}_1$,
${U}_2$
がある.
壷 ${U}_1$には8個の白球と2個の黒球,
壷 ${U}_2$には4個の白球と6個の黒球
が入っているとする
(cf. Table 2.2, Figure 2.8).
次のような現象(a)を考える:
| (a): | 壷 $U_2$から1つの球を取り出すとき,
その球が
$
\left[\begin{array}{ll}
白
\\
黒
\end{array}\right]
$
である確率は
$
\left[\begin{array}{ll}
0.4
\\
0.6
\end{array}\right]
$
である.
|
ここで,この日常言語の文言(a)を測定理論(言語ルール1 ( 純粋測定: $\S$2.7))の
言葉遣いで記述することを考える.
ここで,
\begin{align*}
古典系の基本構造
[C_0(\Omega ) \subseteq L^\infty (\Omega, \nu ) \subseteq B(L^2 (\Omega, \nu ))]
\end{align*}
を考えよう.
$\Omega = \{ {\omega}_1 , {\omega}_2
\}$
として,
離散距離空間$(\Omega, d_D)$を考えて,
可換$C^*$代数$C_0(\Omega)$を得る.
また,測度空間
$(\Omega, 2^{\Omega}, \nu )$を
\begin{align*}
\nu(\{\omega_1 \} )=1, \quad
\nu(\{\omega_2 \} )=1
\quad(\mbox{別に,$\nu(\{\omega_1 \} )=a, \quad
\nu(\{\omega_2 \} )=b$でも可($a,b>0$)})
\end{align*}
として,
可換$W^*$代数$L^\infty (\Omega, \nu)$を得る.
したがって, 純粋状態空間は
\begin{align*}
{\frak S}^p (C_0(\Omega)^*)= \{ \delta_{\omega_1} , \delta_{\omega_2} \}
\approx
\{ \omega_1, \omega_2 \}=\Omega
\end{align*}
となる.
ここで, ,
\begin{align*}
U_1 \quad \cdots \quad
\mbox{"状態$\delta_{\omega_1}$をもつ壷"},
\qquad
U_2 \quad \cdots \quad
\mbox{"状態$\delta_{\omega_2}$をもつ壷"}
\end{align*}
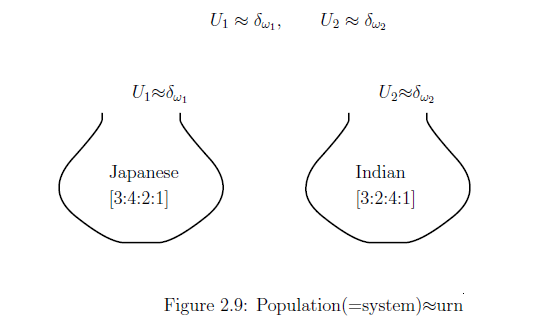
として, 次の同一視を考える:
\begin{align*}
U_1 \approx
\delta_{\omega_1}, \qquad
U_2 \approx
\delta_{\omega_2} \quad
\quad
\end{align*}
さて、"$w$" = "white"$\!\!,\;$ "$b$" = "black"$\!\!\;$,
$X=\{w,b\}$とおいて、観測量 ${\mathsf O} \big(\equiv (X \equiv \{w,b\}, 2^{\{w,b\}}, F) \big)$ in $L^\infty (\Omega)$を次のように定義する:
\begin{align}
[F(\{w\})](\omega_1) = 0.8,& \qquad \qquad [F(\{b\})](\omega_1) = 0.2,
\\
[F(\{w\})](\omega_2) = 0.4,& \qquad \qquad [F(\{b\})](\omega_2) = 0.6.
\end{align}
よって、測定$ {\mathsf M}_{L^\infty (\Omega)} ({\mathsf O} ,
S_{[ \delta_{\omega_2}]})$を得る。
ここで、
言語ルール1 ( $\S$2.7)の言葉遣いで、次の翻訳ができる。
| (b): | 測定${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O} , S_{[ \delta_{\omega_2}]})$によって測定値 ${b}$が得られる
確率は
\begin{align}
F(\{b\})(\omega_2) = 0.4
\end{align}
である。
|
結局、次の翻訳を得た
\begin{align}
\underset{\mbox{ (日常言語)}}{\fbox{文言 (a)}}
\xrightarrow[{\mbox{翻訳}}]{}
\underset{\mbox{ (量子言語)}}{\fbox{文言 (b)}}
\tag{2.70}
\end{align}
| $\fbox{注釈2.5}$ | [$L^\infty (\Omega, \nu )$, or in short, $L^\infty (\Omega)$]
上の例において,
個数測度
$\nu$
(i.e.,
$\nu(\{\omega_1\})=\nu(\{\omega_2\})=1$)
が不可欠というわけではない。
たとえば、
$\nu(\{\omega_1\})=2$,
$\nu(\{\omega_2\})=1/3$
と仮定しても同じ結論を得る。
したがって、測度を省いて、
\begin{align*}
\mbox{
$L^\infty (\Omega, \nu )$
はしばしば
$L^\infty (\Omega)$
と省略される
}
\end{align*}
と記すこともある
|
| $\fbox{注釈2.6}$ |
例2.34[壺問題]の(a),
すなわち,
| $(\flat_1)$ | 「壷 $U_2$から1つの球を取り出すとき,
その球が
"白"
である確率は$0.4$である
|
は保証されているわけではない.
測定理論は言語なので,
| $(\flat_2)$ | もし(a)のような現象があったならば,それは
(b)のように記述すべきで、 これが「科学的な記述」である。
|
と言っているだけにすぎない。
また当然のことだが,
数学だけから「(非数学的概念である)確率」が求まることはない.
たとえば,次の$(\sharp_1)$,
$(\sharp_2)$
等は正しいとは言えない:
| $(\sharp_1):$ | 集合$\{1,2,3,4,5\}$
から,一つの数を選んだとき,
その数が偶数である
確率は$2/5$である
| | $(\sharp_2):$ |
閉区間$[0,1]$
内から,
実数$x$
を選んだとき,
「$x \in [a,b]( \subseteq [0,1] )$」
となる確率は,
$|b-a|$である
|
このように
「
(世界と断絶している)数学だけから確率を導出する
」ことの論拠がないことは,
ベルトランの逆理
(cf. 9.12節
)
としてよく知られている.
したがって,
「無作為に」とか
「ランダムに」
等の言葉を枕詞のように付け加えるのが普通だが,
本書では,
「常識的にわかること」として省略した.
|
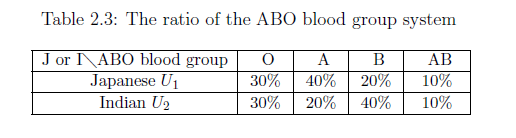
 例 2.35 [血液型]
例 2.35 [血液型]
日本人全体の集合を${U}_1$,
インド人全体の集合を${U}_2$
とする.
日本人の血液型[O:A:B:AB]の比は,[3:4:2:1]
で,
インド人の血液型[O:A:B:AB]の比は,[3:2:4:1]
である.
次の現象を考えよう:
| (a): | インド人全体$U_2$から無作為に一人を選んで,
その人の血液型が
$
\left[\begin{array}{ll}
O
\\
A
\\
B
\\
AB
\end{array}\right]
$
である確率は
$
\left[\begin{array}{ll}
0.3
\\
0.2
\\
0.4
\\
0.1
\end{array}\right]
$
である
|
ここで,この日常言語の文言(a)を測定理論
の
言葉遣いで記述することを考える.
$\Omega = \{ {\omega}_1 , {\omega}_2
\}$
として,
離散距離空間$(\Omega, d_D)$を考えて,
可換$C^*$代数$C_0(\Omega)$を得る.
さて,
\begin{align*}
\mbox{
古典系の基本構造
$[C_0(\Omega ) \subseteq L^\infty (\Omega, \nu ) \subseteq B(L^2 (\Omega, \nu ))]$
}
\end{align*}
を考えよう.
したがって, 純粋状態空間は
\begin{align*}
{\frak S}^p (C_0(\Omega)^*)= \{ \delta_{\omega_1} , \delta_{\omega_2} \}
\end{align*}
となる.
ここで, ,
\begin{align*}
&
\delta_{\omega_1} \quad \cdots \quad
\mbox{"日本人全体の集合$U_1$(母集団)の状態"}
\qquad
\\
&
\delta_{\omega_2} \quad \cdots \quad
\mbox{"インド人全体の集合$U_2$(母集団)の状態"},
\end{align*}
次の同一視を考える:
血液型観測量 ${\mathsf O}_{\mbox{ BT}} = ( \{ O, A,B,AB \}, 2^{\{ O, A,B,AB \} } , F_{{{\mbox{ BT}}}})$ in $L^\infty (\Omega, \nu )$
を次のように定義する。
\begin{align}
& [F_{\mbox{ BT}}(\{ O \})](\omega_1)= 0.3, & \quad & [
F_{\mbox{ BT}}(\{\})](\omega_1)= 0.4
\nonumber
\\
& [F_{\mbox{ BT}}(\{ B \})](\omega_1)= 0.2, & \quad & [
F_{\mbox{ BT}}(\{ AB \})](\omega_1)= 0.1
\tag{2.71}
\end{align}
\begin{align}
& [F_{\mbox{ BT}}(\{ O \})](\omega_2)= 0.3, & \quad & [F_{\mbox{ BT}}(\{\})]
(\omega_2)= 0.2
\nonumber
\\
& [F_{\mbox{ BT}}(\{ B \})](\omega_2)= 0.4, & \quad & [F_{\mbox{ BT}}(\{ AB \})]
(\omega_2)= 0.1
\tag{2.72}
\end{align}
したがって、測定${\mathsf M}_{{L^\infty (\Omega, \nu )}} ({\mathsf O}_{{{\mbox{ BT}}}} , S_{ [{\delta_{\omega_2}}]})$を得て、
上の(a)は次のように翻訳できる。
| (b): |
測定
${\mathsf M}_{{L^\infty (\Omega, \nu ) }} ({\mathsf O}_{\mbox{ BT}} ,
S_{ [{\delta_{\omega_2}}]})$によって測定値$
\left[\begin{array}{ll}
O
\\
A
\\
B
\\
AB
\end{array}\right]
$が得られる
確率は、
$
\left[\begin{array}{ll}
{_{C_0(\Omega)^*}}
\Big(
\delta_{{\omega_2}},
F_{{{\mbox{ BT}}}}(\{O\})
\Big){_{L^\infty(\Omega, \nu )}}
=
[F_{{{\mbox{ BT}}}}(\{O\})](\omega_2)
=
0.3
\\
{_{C_0(\Omega)^*}}
\Big(
\delta_{{\omega_2}},
F_{{{\mbox{ BT}}}}(\{A\})
\Big){_{L^\infty(\Omega, \nu )}}
=
[F_{{{\mbox{ BT}}}}(\{A\})](\omega_2)
=
0.2
\\
{_{C_0(\Omega)^*}}
\Big(
\delta_{{\omega_2}},
F_{{{\mbox{ BT}}}}(\{B\})
\Big){_{L^\infty(\Omega, \nu )}}
=
[F_{{{\mbox{ BT}}}}(\{B\})](\omega_2)
=
0.4
\\
{_{C_0(\Omega)^*}}
\Big(
\delta_{{\omega_2}},
F_{{{\mbox{ BT}}}}(\{AB\})
\Big){_{L^\infty(\Omega, \nu )}}
=
[F_{{{\mbox{ BT}}}}(\{AB\})](\omega_2)
=
0.1
\end{array}\right]
$
で与えられる。
|
| $\fbox{注釈2.7}$ | 本節では,簡単な例を,物々しく(しかも,
まどろっこしく)書いているように思うかもしれない.
「これでは,小学生の本ではないか?」と思うかもしれない.
しかし,言語的科学観においては、我々が頼れるのは、
| $\bullet$ | $\left\{\begin{array}{ll}
\mbox{言語ルールに忠実
}
\\
\\
\mbox{人間の言語能力の信頼
}
\end{array}\right.
$
|
だけである.
| $\quad$ |
もしも読者がこれとは別の書き方を発見したならば
(すなわち,言語ルール1(測定: $\S$2.7)の一語でも一句でも本質的な意味で改変や何かを付け加えることができたならば),
量子力学以上のものを作り上げたことに
等しく,
科学史上最大級の呪文の発見
と評価されるだろう.
|
これにはぜひ挑戦してもらいたいが、
前にも($\S$1.1の主張1.1で)述べたように,
「量子言語」が最終到達点であると考えている.
現状では,これ以外のアイデアを
知らないからである.
もちろん、それでも挑戦してもらいたい。
|


 例 2.35 [血液型]
例 2.35 [血液型]