例2.36
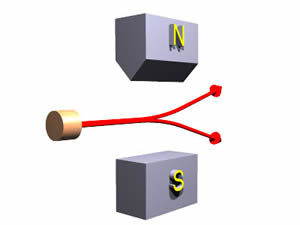
電子は磁場の中
(すなわち,
$N$極と
$S$極の間
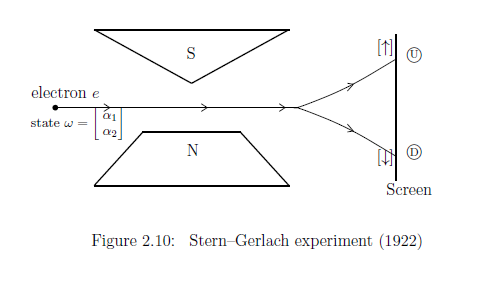
)を通り抜けると,図2.10のように,
上かまたは下に曲がる.それをスクリーンに設置したガイガーカウンターで
検出するシュテルン=ゲルラッハの実験について考えよう.
さて,
㊤(up)か㊦(down)のどちらの
ガイガーカウンターが鳴るだろうか?
基本構造
$[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]$を
量子系として,
\begin{align*}
\textcolor{red}{\mbox{
$[{\mathcal C}({\mathbb C}^2 ) \subseteq \overline{{\mathcal C}({\mathbb C}^2)} \subseteq B({\mathbb C}^2)]$
}
}
\end{align*}
を考えよう.
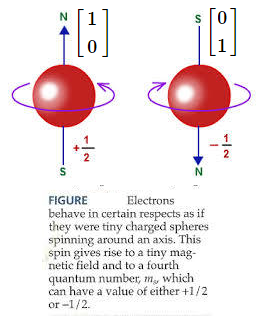
有限次元なので, ${\mathcal C}({\mathbb C}^2)=\overline{{\mathcal C}({\mathbb C}^2)}=B({\mathbb C}^2) $であることに注意しよう. 状態空間${\frak S}^p({{\mathcal C}({\mathbb C}^2)}^*)$ $=\{ \rho = | u \rangle \langle u | \; : \; \|u \|_{{\mathbb C}^2}=1 \}$ であり, 電子$e$のスピン状態$\rho$は状態空間${\frak S}^p({{\mathcal C}({\mathbb C}^2)}^*)$ の元で表現できる.
ここで, $ u = \left[\begin{array} \; \alpha_1 \\ \; \alpha_2 \end{array}\right] $とおく ( ここに, $\|u \|^2 = |\alpha_1|^2 +|\alpha_2|^2 =1$ ). また,測定値空間を$X=\{\uparrow ,\downarrow \}$ として, 「電子の$z$-軸方向のスピン」の観測量 ${\mathsf O} =(X,2^X, F^z )$ は次のように定まる: \begin{align} & F_z (\{ \uparrow \}) = \left[\begin{array}{ll} 1 & 0 \\ 0 & 0 \end{array}\right] , \quad F_z (\{ \downarrow \}) = \left[\begin{array}{ll} 0 & 0 \\ 0 & 1 \end{array}\right] , \quad F_z (\emptyset) = \left[\begin{array}{ll} 0 & 0 \\ 0 & 0 \end{array}\right] , \quad F_z (\{ \uparrow ,\downarrow \}) = \left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right] . \\ & \tag{2.73} \end{align} このようにして, 量子測定 ${\mathsf M}_{B({\mathbb C}^2)}({\mathsf O}, S_{[\rho(=| u \rangle \langle u |)]})$ を得る.このとき, ボルンの量子測定理論 [(量子版)言語ルール1( 純粋測定: $\S$2.7)]により, 次が言える:
| $(\sharp):$ | 量子測定${\mathsf M}_{B({\mathbb C}^2)}({\mathsf O}, S_{[\rho(=| u \rangle \langle u |)]})$ によって, \begin{align*} \mbox{測定値} \left\{\begin{array}{ll} \mbox{$\uparrow$} \\ \mbox{$\downarrow$} \end{array}\right\} \mbox{が得られる確率} \mbox{は} \left\{\begin{array}{ll} \langle u, F^z(\{ \uparrow\}) u \rangle =|\alpha_1|^2 \\ \\ \langle u, F^z(\{ \downarrow\}) u \rangle = |\alpha_2|^2 \end{array}\right\}\mbox{である.} \end{align*} |
すなわち,
| $(\flat)$ | \begin{align*} & \mbox{スピン状態$u$ $(= \left[\begin{array}{ll} \; \alpha_1 \\ \; \alpha_2 \end{array}\right] \in {\widehat \Omega} )$をもつ電子$e$が磁場を通ったとき}, \left\{\begin{array}{ll} \mbox{㊤} \\ \mbox{㊦} \end{array}\right\} の \\ & ガイガーカウンター \mbox{が鳴る確率} \mbox{は} \left\{\begin{array}{ll} \big[ \overline{\alpha}_1 \;\;\; \overline{\alpha}_2 \big] \left[\begin{array}{ll} 1 & 0 \\ 0 & 0 \end{array}\right] \left[\begin{array}{ll} \; \alpha_1 \\ \; \alpha_2 \end{array}\right] =|\alpha_1|^2 \\ \\ \big[ \overline{\alpha}_1 \;\;\; \overline{\alpha}_2 \big] \left[\begin{array}{ll} 0 & 0 \\ 0 & 1 \end{array}\right] \left[\begin{array}{ll} \; \alpha_1 \\ \; \alpha_2 \end{array}\right] =|\alpha_2|^2 \end{array}\right\} \\ & \mbox{である.} \end{align*} |
スピン観測量をまとめておく.
測定値空間を$X=\{\uparrow ,\downarrow \}$
として,
[$z$-軸方向のスピン観測量]
「電子の$z$-軸方向のスピン」の観測量
${\mathsf O}_z =(X,2^X, F^z )$
は次のように定まる:
\begin{align*}
F^z( \{ \uparrow \})
=
\left[\begin{array}{ll}
1 & 0 \\
0 & 0
\end{array}\right]
,
\quad
F^z( \{ \downarrow \})
=
\left[\begin{array}{ll}
0 & 0 \\
0 & 1
\end{array}\right]
\end{align*}
[$x$-軸方向のスピン観測量]
「電子の$x$-軸方向のスピン」の観測量
${\mathsf O}_x =(X,2^X, F^x )$
は次のように定まる:
\begin{align}
F^x( \{ \uparrow \})
=
\left[\begin{array}{ll}
1/2 & 1/2 \\
1/2 & 1/2
\end{array}\right]
,
\quad
F^x( \{ \downarrow \})
=
\left[\begin{array}{ll}
1/2 & -1/2 \\
-1/2 & 1/2
\end{array}\right]
\tag{2.74}
\end{align}
[$y$-軸方向のスピン観測量] 「電子の$y$-軸方向のスピン」の観測量 ${\mathsf O}_y =(X,2^X, F^y )$ は次のように定まる: \begin{align} F^y( \{ \uparrow \}) = \left[\begin{array}{ll} 1/2 & -i/2 \\ i/2 & 1/2 \end{array}\right] , \quad F^y( \{ \downarrow \}) = \left[\begin{array}{ll} 1/2 & i/2 \\ -i/2 & 1/2 \end{array}\right] \tag{2.75} \end{align} ここで \begin{align*} {\hat S}_x = F_x(\{\uparrow \}) - F_x(\{\downarrow \}), \quad {\hat S}_y = F_y(\{\uparrow \}) - F_y(\{\downarrow \}) , \quad {\hat S}_z = F_z(\{\uparrow \}) - F_z(\{\downarrow \}) \end{align*} とするとき, 次の交換関係は, 注目に値する. \begin{align} {\hat S}_y {\hat S}_z- {\hat S}_z {\hat S}_y =2i {\hat S}_x, \quad {\hat S}_z {\hat S}_x- {\hat S}_x {\hat S}_z =2i {\hat S}_y, \quad {\hat S}_x {\hat S}_y- {\hat S}_y {\hat S}_x =2i {\hat S}_z \tag{2.76} \end{align} 「注目」というより、この交換関係は数学的に美しすぎる。
- 数学が先行して、それに量子力学が追従してる
これに納得するためには、
- 量子言語は、神学である
- シュテルン=ゲルラッハの実験は、「光より速い何か」の存在を示唆している
