目次:

3.1.1 言語ルール1 (測定: $\S$2.7)の復習

前章で紹介した言語ルール1 (測定)を再掲しておく。 言語ルール1(測定: $\S$2.7)は、ボルンの「量子測定理論」の言語化(=ことわざ化=数学的一般化)とみなすことができる。
3.1.1 言語ルール1 (測定: $\S$2.7)の再掲

あらゆるシステムはある基本構造 $[ {\mathcal A} \subseteq \overline{\mathcal A}]_{B(H)}$内で定式化できる. $[ {\mathcal A} \subseteq \overline{\mathcal A}]_{B(H)}$ 内で定式化された$W^*$-測定 ${\mathsf M}_{\overline{\mathcal A}} \big({\mathsf O}{{=}} (X, {\cal F} , F), S_{[\rho] } \big)$ $\Big($ または, $C^*$-測定} ${\mathsf M}_{{\mathcal A}} \big({\mathsf O}{{=}} (X, {\cal F} , F), S_{[\rho] } \big)$ $\Big)$ を 考えよう．


このとき, $W^*$-測定 ${\mathsf M}_{\overline{\mathcal A}} \bigl({\mathsf O} , S_{[\rho] } \bigl)$ $\Big($ または, $C^*$-測定 ${\mathsf M}_{{\mathcal A}} \big({\mathsf O}{{=}} (X, {\cal F} , F), S_{[\rho] } \big)$ $\Big)$ により得られる 測定値$ x$ $(\in X )$ が， $ \Xi $ $(\in {\cal F})$ に属する{確率}は， (もし$F(\Xi)$が$\rho$で本質的連続ならば) $\rho( F(\Xi))$ $(\equiv _{{{\mathcal A}^*}}(\rho, F(\Xi) )_{\overline{\mathcal A}} )$ で与えられる

次に注意せよ。

$(A):$言語ルール1(測定: $\S$2.7)は一種の呪文 (i.e., お経, 魔法の言葉, 形而上学的命題)で 実験検証は不可能である。

よって、これはカントの純粋理性批判の 「アプリオリな総合判断」 に対応すると考えたくなる。 したがって、

$(B):$ 呪文(= 言語ルール1) を丸暗記して、試行錯誤しながらその使い方を上達していくものと思えばよい。
しかしながら,
$(C_1):$呪文(= 言語ルール1)の上達を速くしたいならば、量子言語の使い方ののマニュアルがあった方がよい。このマニュアルのことを「言語的解釈」よぶ。
すなわち、
$(C_2):$ 言語的解釈=量子言語の使い方ののマニュアル

である。

注意点は、
$(C_3):$ 日常言語は、オギャーと生まれた赤ん坊のときは白紙(=タブラ・ラーサ)で、それから試行錯誤で上達するわけであるが、 量子言語は、白紙(=タブラ・ラーサ)から始めるのではなくて、言語ルール1から始めて上達する。
ことである。

カントや彼の称賛者たちが、「純粋理性批判」において何を言いたかったのか、または、何を読み取ったのかは不明だが、 「アプリオリな総合判断=言語ルール」以外の理解の仕方を知らない。

それにしても、 近代哲学の華である デカルトからカントまで流れ： \begin{align} \underset{\mbox{[二元論的観念論]}}{\mbox{デカルト哲学}}\longrightarrow \left\{\begin{array}{ll} \textcolor{blue}{\underset{\mbox{[言語ルール]}}{\mbox{大陸合理主義}}} \\ \\ \textcolor{red}{\underset{\mbox{[言語的解釈]}}{\mbox{イギリス経験主義}}} \end{array}\right\} \longrightarrow \underset{\mbox{[量子言語]}}{\mbox{カント哲学}} \end{align} は、一体なんだったのだろうか？ ,br> また、
$(C_4):$ アプリオリな総合判断の具体例を提示しなかった 純粋理性批判がなぜ熱狂的な称賛を得たのか？ しかも、全く役に立たないにも拘わらずである。


著者にとっては謎である。

  • デカルト＝カント哲学など無くてもよかった
    とか
    あったことが不思議

と言う意見に反論するつもりはないが、折角あるのだから、デカルト＝カント哲学を利用しつつ量子言語を説明するという方針にする。

3.1.2: デカルト図式(言語的解釈の基本図式)

二つの呪文(=言語ルール1と2)を「数学込みの丸暗記」をして, これを, 20年ぐらい試行錯誤して使い続けていれば, 自然と「使い方のテクニック」を会得できるかもしれないが, やはり, 「使い方のマニュアル」のようなものがあった方が手っ取り早い. すなわち, \begin{align*} \mbox{ 「呪文の使い方のマニュアル」が, 「言語的解釈」である. } \end{align*} 以下に, これ(=言語的解釈)を説明しよう.

「言語ルール1(測定: $\S$2.7)」の文章中に, 「測定」という言葉が　出てくるのだから,

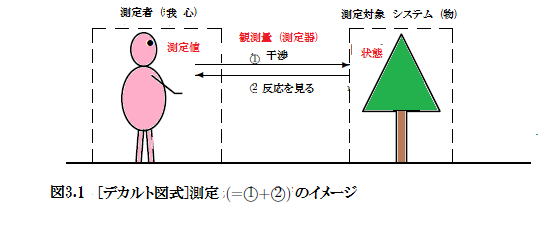
$(C_5):$「測定者」と「測定対象」からなる二元論
と考えたくなる. しかしながら, 「測定者」と「測定対象」だけでは, 不十分で, 「測定器」がなければ, 「測定」は成立しない. したがって, 測定のイメージは，図3.1[デカルト図式]のようになる.



上で,
$(D_1):$測定= "①干渉" + "②そのリアクション"
であり、"測定"とは 「測定者と測定対象の相互作用」 である。 しかしながら, この"相互作用"を記述する運動方程式は存在しないと考える。 (もしそのような運動方程式が存在すれば、二元論は不要で一元論だけで済ますことができる). よって、
$(D_2):$ 測定理論(=量子言語)では、相互作用と言わないで、 測定 と言う。

したがって, 混乱を避けるために, 図3.1の中では、 相互作用 "①と①"　を書かない方が良かったかもしれない。 また、
$(D_3):$測定者(=脳)なくしては、測定値はないわけで、この意味では、 測定理論のキーワードは、 (cf. 注釈3.1 later): \begin{align} \underset{\mbox{ (測定者, 脳, 心)}}{\fbox{測定値}}, \quad \underset{\mbox{ (温度計, 目, 耳, 感覚器, 身体,測定器, 北極星)}}{\fbox{観測量 (= 測定器 )}}, \quad \underset{\mbox{ (測定対象)}}{\fbox{状態}}, \end{align} である。　この意味では、二元論ではなくて、
  • 三元論
である。たとえば、二つの二元論(「物心二元論」と「心身二元論」)があるという事実は、このあたりの混乱を表している。 しかしながら、 慣習にしたがって、この講義では、「二元論」と言う。

3.1.3: 言語的解釈 $(E_1)-(E_7)$

言語的解釈は"言語ルール1と2の使い方のマニュアル"である。 マニュアルならば、詳しく書けば切りがないわけで、この本に書くことすべてが言語的解釈であるとも言える。 しかしながら, ここでは、重要で使い出があるものを、以下の(E)として、列挙しておく。　この中で、特に重要なのは、
  • 測定は一回だけ
である。
(E):言語的解釈 (=量子言語の使い方のマニュアル)
デカルト図式3.1を念頭に置いて、言語的解釈というマニュアル(E$_1$)-(E$_7$)の下に、 言語ルール1と2の言葉遣いですべての現象を記述せよ！
$(E_1):$「我(=測定者)」と「物(=測定対象)」の２つから成る 二元論で， 当然， 「我(=測定者)」と「物(=測定対象)」 は完全分離で、この二つを混同してはならない. 喩えて言うならば， 「観客は舞台に上がらない」 である。　「我」が「我」を測定するなどという設定を考えてはならない(cf. 8.4節：コギト命題).
$(E_2):$ 「物(=測定対象)」の方には，時間・空間を想定するが， 「我(=測定者)」には，時間・空間を想定しない． したがって，測定理論には，「測定時刻,測定後,測定した瞬間」,「時制」の概念がないので， 測定理論で記述される諸科学にも「時制」の概念はない
$(E_3):$ 測定は, 「我(=測定者)」と「物(=測定対象)」の相互作用とイメージしてもよいが， 相互作用のことを陽には言わない
$(E_4):$ 測定は一回だけ. しかも， 測定後の状態は考えない．
$(E_5):$ 測定なくして，確率なし
$(E_6):$ 状態は変化しない.
等. いろいろとあって雑多な感じがするかも しれないが，それは「公理・ルール」というより「言語ルールの使い方の指示(マニュアル)」 であるためで,　細かいことを言えば,切りがない.　極端な(正確な)言い方をすれば, 「本書で述べることすべてが,言語的コペンハーゲン解釈」 であるとも言えるし、 逆に 「マニュアルなどなくても、試行錯誤を重ねて会得せよ」 とも言える。
また,本書の主張($\S1.1$の主張1.1)は
  • 二元論的観念論(="デカルト=カント哲学")の最終到達点が,量子言語
なので、
$(E_7):$ギリシャ以来の哲学者たちの金言の多くは,言語的コペンハーゲン解釈の一部になっている
と思ってもよいだろう.
上の(E$_7$)は信じ難い奇跡であるが,
$(F_1):$哲学の本来の目的は,「世界記述」であったはずで,そうならば,「量子言語の目的」と同じなのだから,
$(F_2):$　デカルト=カント哲学の方法と量子言語の方法は共に、 二元論的観念論で同じなのだから、
  • 　哲学者たちの至言 $\approx$ 言語的コペンハーゲン解釈
と考えない方がおかしい。
$\fbox{注釈3.1}$ 　比喩として適切かどうか自信はないけれど、一言でザックリと言うと、
  • 映画を観たときの感想文のように語れ!!!
である。　これをもうすこし具体的に説明すると、
  • 私(=一人称=測定者＝観客)の目線で語る。　感想文ならば、　「私(=一人称=測定者＝観客)の目線」でしょう。　もちろんのことであるが、　観ていないのに、「感想文」を書いてはいけない。　 (このブログでは、これをデカルトの「我の発見(=二元論の発見)」とした。　バークリーは「存在するとは、知覚されることである」と主張した。　このことは、神(=三人称=報道アナウンサー)の目線で語る物理学(すなわち、「映画のあらすじを述べるように語れ」)と対比すべきである。　アインシュタインは、「月は見ていなくても存在する」といって、「私目線」に反対した。　)

  • 二つの映画を同時に観ることはできない(普通はしない)。　そうだとすれば、私(=一人称=測定者＝観客)は二つの測定を同時に行うことは普通はできない。　すなわち、 「測定は一回だけ」 となる。 (この比喩は強引すぎるかもしれないが、量子力学では粒子の位置の測定と運動量の測定を同時に行うことはできない。　これを思い出せばよい。 )

  • 映画だとすれば、私(=一人称=測定者＝観客)がスクリーンの中に飛び入りすることが不可能であることは、当然である。　私が映画のストーリーを変えることはできない。　すなわち、観客は舞台に上がってはならない。 (しかし、　量子力学の研究者の一部は、射影仮説「測定したことによって現象が変化する(波動関数が収縮する)という意見」を主張するが、　これは誤りと考える。　また、コギト命題「我思う、故に我あり」もあいまいな命題である。　「我」が客席にいるのかスクリーンにいるのか(故意に)混同させて、　科学的命題を逸脱しているからである。　事実、　コギト命題が科学の中で使われたことは一度もない。　 )
  • 私(=一人称=測定者＝観客)には、時空は無いとする。　「時制(過去、現在、未来)も無い」と言い切る。　 (映画を何処で観たか、映画館かDVDか? いつ観たか？　昼か夜か？　昨日か一年前か？　等は問わないとする。　アウグスティヌスからベルクソンに至る「主観時間」の考察は、科学の立場からは、「時制の非存在」を言い切る勇気の欠如の産物と考える。　もちろん、文芸の立場からならば、「主観時間」の議論を楽しむ文化はあってもよい。 )
である。



次の図式($\S1.1$の主張1.1)を再掲しておく。
  • 世界記述史の中での量子言語の位置
上で、二元論的観念論の系譜：
について、皮肉な言い方をするならば、
$\bullet$二元論的観念論の哲学者たちは、 「言語ルール」を知らずに、「言語ルールの使い方のマニュアル」を作り続けてきた
と言える。
たとえば,, "測定は一回だけ"と"状態は動かない" はパルメニデの発見である。

$ \left\{\begin{array}{l} \mbox{ There is no　"plurality", but only "one".多はない。あるのは一だけ } \\ \\ \mbox{ And therefore, there is no movement.　運動は存在しない} \end{array}\right. $

したがって、, パルメニデス (born around BC. 515) は、言語的解釈の最古の発見者と見なしたい

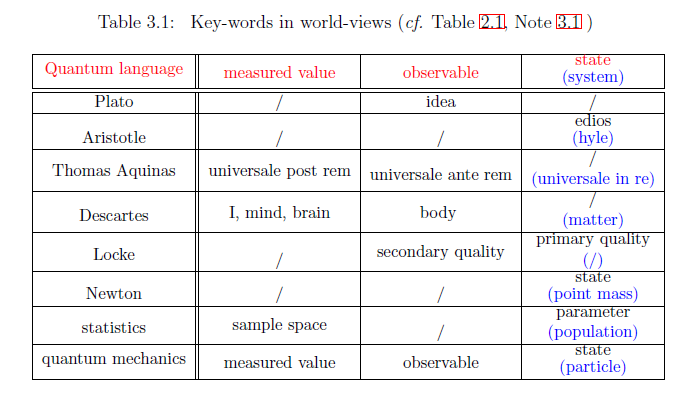
また、次表を参考になるだろう。

「存在論」についてよく知っているわけではないが、個人的には、 「キーワード=存在」と考える。よって、世界記述法が変われば、「存在」も変わる。世界記述法が宣言されていない議論で、
$\bullet:$「美」は存在するか？
$\bullet:$「数学」は存在するか？
等は意味をなさない。
$\fbox{注釈3.1}$上の表では、ニュートン力学の部分が一番わかりやすい。 アリストテレスはニュートンと発想は同じで一元論である。
"プラトン　イデア" を"絶対基準(メートル原器のようなもの)"とみなしてよいならば、ホワイトヘッドの言葉：
  • 西洋の全ての哲学はプラトン哲学への脚注に過ぎない
すなわち、それそれの哲学はそのときどきの単なるブームというわけではなくて、
  • 西洋哲学は、系譜(3.2)のように継続的に進化してきた
と理解することができる。 上の表3.1において、観測量(observable)の概念を有する世界記述法が二元論である。
(3.1)式で見たように, "観測量"="測定器"="身体(感覚器)" であるが、いろいろなバリエイションがあって、たとえば、観測量(observable)の例として、 $$ \mbox{目, 耳, 望遠鏡, 顕微鏡, 方位磁石, 北極星, 等. } $$

である。 "方位磁石"が観測量(=測定器)の一種ならば、 "北極星"もそうだろう.
また、 「脳(brain)無くして、測定値(measured value)無し」なのだから、 対応： "測定値 $\longleftrightarrow$ 脳(=心)" も了解できるだろう。
スコラ哲学を知っているわけではないが、 三つのキーワード ("post rem (事の後に)", "ante rem　(事の前に)", "in re (事の中に)")の居場所を 三元論の中で見つけるとすれば、上の表のようになるだろう。





P.S. 結局、右図は次を主張している：
$(\sharp_1):$一元論的実在論を追究するのが、物理学の中心的テーマ
$(\sharp_2):$二元論的観念論を追究するのが、哲学の中心的テーマ
すなわち、
  • 哲学も、意外と一貫性を貫いている
である。
もちろん、 物理学者のなかで、統一理論に関わっている物理学者は滅多にいないわけで、 たいていは、応用に関わっている。 これと同じ意味で、二元論的観念論に関わっていない哲学者が多数派だったとしても、 不思議な話ではない。 そうだとしても、「中心」であることに変わりはない。