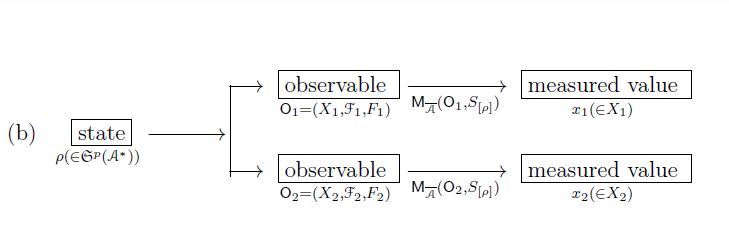3.3.1: 観測量は一つだけ (⇐ 測定は一回だけ )
例2.31 (in $\S$2.7)
と
例2.32 (in $\S$2.8)
を念頭に置いて,
たとえば,次のような「測定」を
考えよう:
定義3.11[直積可測空間]
各
$k =1,2,\ldots,n$
に対して,
可測空間
$(X_k , $
${\cal F}_k )$を
考える.
$X_k$
$(k=1,2,\ldots,n )$
の
直積空間
${{{\times}}}_{k=1}^n X_k$
を
\begin{align*}
{{{\times}}}_{k=1}^n X_k
=
\{ (x_1, x_2,\ldots, x_n ) \;|\; x_k \in X_k
\;\;
(k=1,2,\ldots,n )\}
\end{align*}
によって定める.
同様に,
$\Xi_k
(
\in
{\cal F}_k
)$
$(k=1,2,\ldots,n )$
の
直積
${{{\times}}}_{k=1}^n \Xi_k$
を
\begin{align*}
{{{\times}}}_{k=1}^n \Xi_k
=
\{ (x_1, x_2,\ldots, x_n ) \;|\; x_k \in \Xi_k
\;\;
(k=1,2,\ldots,n )\}
\end{align*}
で定義する.
更に,
直積空間
${{{\times}}}_{k=1}^n X_k$
内の$\sigma$-集合体
$\boxtimes_{k=1}^n{\cal F}_k$
を
と定めて,これを
直積集合体
と呼び,
$({{{\times}}}_{k=1}^n X_k , \boxtimes_{k=1}^n{\cal F}_k)$
を
直積可測空間
と呼ぶ.
$(X,{\cal F})=(X_k,{\cal F}_k)$
$(k=1,2,\ldots,n)$
のとき,
直積空間
${{{\times}}}_{k=1}^n X_k$
を
$X^n$
と記し,
直積可測空間
$({{{\times}}}_{k=1}^n X_k ,$
$ \boxtimes_{k=1}^n{\cal F}_k)$
を$(X^n,{\cal F}^n)$
と書く.
定義3.12 [同時観測量, 同時測定]
基本構造を$[{\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]$
として,
各
$k =1,2,\ldots,n$
に対して,
基本代数$\overline{\mathcal A}$
内の
観測量${\mathsf O}_k$
$=$
$(X_k , $
${\cal F}_k , $
$F_k{})$
考える.
$({{{\times}}}_{k=1}^n X_k , \boxtimes_{k=1}^n{\cal F}_k)$
を直積可測空間とする.
さて,
$\overline{\mathcal A}$
内の観測量
$\widehat{\mathsf O}$
$=$
$({{{\times}}}_{k\in K } X_k ,$
$ \boxtimes_{k=1}^n{\cal F}_k , $
$\widehat{F}{})$
は次を満たすとする:
\begin{align}
{\widehat F}(\Xi_1 \times \Xi_2 \times \cdots \times \Xi_{n}{})
&
=
F_1 (\Xi_1{})
\cdot
F_2 (\Xi_2{})
\cdots
F_n (\Xi_{n}{})
\nonumber
\\
&
(
\forall \Xi_k \in {\cal F}_k \;
(k=1,2,\ldots,n ))
\label{eq3.11}
\end{align}
このとき,
この観測量
$\widehat{\mathsf O}$
$=$
$({{{\times}}}_{k=1}^n X_k , \boxtimes_{k=1}^n{\cal F}_k , \widehat{F}{})$
を,
$\{{\mathsf O}_k\}_{k=1}^n$
の
同時観測量
と呼ぶ.
$\widehat{\mathsf O}$
$=$
$
{{{\times}}}_{k=1}^n{\mathsf O}_k$,
$\widehat{F}$
$=$
$
{{{\times}}}_{k=1}^n{F}_k$
とも記す.
また,
同時観測量$
{{{\times}}}_{k=1}^n{\mathsf O}_k$
の測定,
すなわち,
${\mathsf M}_{\overline{\mathcal A}} ({{{\times}}}_{k=1}^n{\mathsf O}_k, S_{[\rho]})$
を
同時測定
と呼ぶ.
もちろん、
しかし,
$\overline{\mathcal A}$が可換$W^*$代数ならば
(すなわち,
$\overline{\mathcal A}=L^\infty (\Omega)$ならば
),
存在する.
$\fbox{注釈3.3}$
量子力学の標準解釈では
「測定は一回だけ($\S$3.1の言語的解釈(E$_4$))」
と著者は考える
(いろいろな標準理論があって,「射影仮説」
を認める流儀もあるが).
これが
「量子力学では,測定は一回だけ」
の一応の理由付けである.
しかし, 量子言語という形而上学では理由付けなどなくて,
強いて言うならば,
$(\sharp_1)$
測定すると,測定対象が擾乱されて(
$\S$3.1のデカルト図式(測定のイメージ図)}参照),
状態が変わってしまって
(しかも,
この変化はシュレーディンガー方程式で記述できないので),
次に測定しても,
別の(意味不明な)状態を測定することになってしまう.
である。
言語的解釈が(物理学の)コペンハーゲン解釈に遺伝すると考える, すなわち,
$(\sharp_2)$
「計算がドンドン進む」
とか
「確率論の基本定理(コルモゴロフの拡張定理)との整合性」とか
と考える。
念を押すと、
$\quad$ not "$\fbox{コペンハーゲン解釈}\Longrightarrow
\fbox{言語的解釈}$"
but "$\fbox{言語的解釈} \Longrightarrow\fbox{コペンハーゲン解釈}$"
である。
射影仮説(波動関数の収縮)を認める(物理学の)コペンハーゲン解釈は, 実在論的な方向を放棄して、認識論的になる.
たとえば, つぎを考えよう:
ある波動関数$\phi$の電子があって,
$(\flat_1)$
観測者$A$はある観測量$T$の測定を行って測定値$x$を得たとしよう.
そうならば,
$T$の固有値$x$の固有ベクトル$\psi$へ波動関数が収縮したと思うだろう.
したがって,
「波動関数は客観的ではなくて, 観測者の情報に依存する」
ことになる. もちろん, このようなことは射影仮説(波動関数の収縮)を認めるコペンハーゲン解釈の常識であり, それでも慎重に扱えばパラドックスが生じるわけではない.
しかし, 本書の「観測量」はかなり一般的な設定になっていて, 射影仮説が使えるのはかなり特殊な例外的な場合である. よって, (言語論的)量子言語では, 「測定は一回だけ」で済ませる. 多分, これで困ることは起こらないと信じる. そうでないかもしれないが, その時はその時で考えるとして楽観的に進める.
$(\flat_2)$
また, 観測者$B$は測定をしなかったとしよう. このときは, 当然, 波動関数は不変で元々の$\phi$と思うだろう.
3.3.1: 「観測量(測定器)は一つだけ」と同時測定

$(a):$
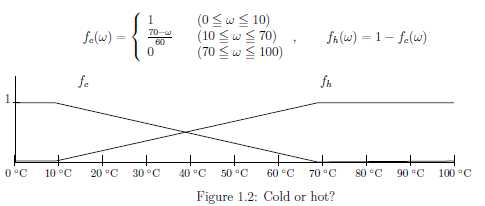
ある一つのコップの中に,温度$\omega$℃の水(お湯)が入っていて,
その水が「冷たいか?熱いか?」
と「約何十℃か」の両方を測定することを
考えたい.
これは$\Omega = [0,100]$
として,
例2.31(in $\S$2.7)
の
測定
${\mathsf M}_{L^\infty ( \Omega )} ( {\mathsf O}_{冷熱}
{{=}}
(\{冷,熱\}
, 2^{\{冷,熱\}}, F_{冷熱} ), S_{[\delta_\omega]} )$
と
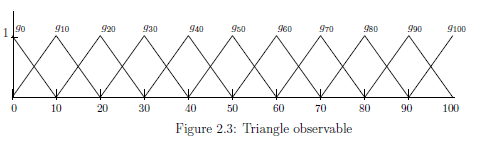
例2.32(in $\S$2.8)
の
測定
${\mathsf M}_{L^\infty ( \Omega )}$
$ ({\mathsf O}_{約}
$
$
{{=}}
({\mathbb N}_{10}^{100} ,$
$
2^{{\mathbb N}_{10}^{100} }, G_{約} ),$
$
S_{[\delta_\omega]} )
$
の2つの測定を
行うことと等しい.
$\bullet$
$
\left\{\begin{array}{l}
\mbox{
$(\sharp_1)$:
${\mathsf M}_{L^\infty ( \Omega )} ( {\mathsf O}_{{{{{c}}}}{{{{h}}}}}
{{=}}
(\{{{{{c}}}},{{{{h}}}}\}
, 2^{\{{{{{c}}}},{{{{h}}}}\}}, F_{{{{{c}}}}{{{{h}}}}} ), S_{[\omega]} )$
in
例 2.31
}
\\
\\
\mbox{
$(\sharp_2)$
:
${\mathsf M}_{L^\infty ( \Omega )}$
$ ({\mathsf O}^{\triangle}
$
$
{{=}}
({\mathbb N}_{10}^{100} ,$
$
2^{{\mathbb N}_{10}^{100} }, G_{約} ),$
$
S_{[\omega]} )
$
in
例 2.32
}
\end{array}\right.
$
しかしながら, 言語的解釈で述べたように,
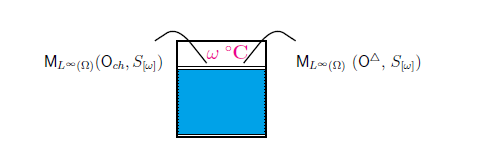
なので、 次の問題を得る。
$\quad$ $\boxtimes_{k=1}^n{\cal F}_k$
は,
$\{
{{{\times}}}_{k=1}^n \Xi_k
\;|\;
\Xi_k \in {\cal F}_k
\;\;
(k=1,2,\ldots,n )
\}$
を含む最小の$\sigma$-集合体
以下に, 「同時測定」の意味を説明する.
しかしながら,言語的解釈(3.1節(E$_4$))
により,
2つの測定
${\mathsf M}_{\overline{\mathcal A}}({\mathsf O}_1,$
$ S_{[\rho]})$
と
${\mathsf M}_{\overline{\mathcal A}}({\mathsf O}_2, S_{[\rho ]})$
を行うことは禁じられているので,
\begin{align*}
\large{\textcolor{red}{\mbox{この(b)は,不可能}}}
\end{align*}
そうならば,
もし2つの観測量${\mathsf O}_1$と${\mathsf O}_2$を
合体させた
同時観測量${\mathsf O}_1\times {\mathsf O}_2$
が存在するならば,同時測定
${\mathsf M}_{\overline{\mathcal A}} (
{\mathsf O}_1
\times
{\mathsf O}_2, S_{[\rho]})$
を
行えばよいと考える.
これを図示すると
| $(c):$ | $ \overset{{}}{\underset{ \rho (\in {\frak S}^p({\mathcal A}^*) ) } {{ \fbox{state(=状態)}}}} \xrightarrow[]{\qquad \qquad} \overset{{}} { \underset{ {\mathsf O}_1 \times {\mathsf O}_2} {{ \fbox{同時観測量 }}} } \xrightarrow[ {\mathsf M}_{\overline{\mathcal A}} ( {\mathsf O}_1 \times {\mathsf O}_2, S_{[\rho]})]{} \overset{{}} { \underset{ (x_1,x_2) (\in X_1 \times X_2 )} {{ \fbox{測定値 }}} } $ |
解答 3.13 [問題3.10の解答] 閉区間$\Omega = [0,100]$ を状態空間とする. ここで, ${\mathcal A}$内の2つの観測量, すなわち, 例2.31の 冷熱-観測量 ${\mathsf O}_{冷熱}= (X {{=}} \{ 冷 , 熱 \}, 2^X, F_{冷熱} )$ と 例2.32の 約-観測量 ${\mathsf O}_{約}= (Y( {{=}} {\mathbb N}_{10}^{100}) , 2^Y, G_{約} )$ を考える. この同時観測量 ${\mathsf O}_{冷熱} \times {\mathsf O}_{約}$ $=$ $(\{ 冷 , 熱 \}\times {\mathbb N}_{10}^{100}, 2^{\{ 冷 , 熱 \}\times {\mathbb N}_{10}^{100}}, F_{冷熱} \times G_{約} )$ を定めて, 同時測定 ${\mathsf M}_{{L^\infty (\Omega) }}({\mathsf O}_{冷熱} \times {\mathsf O}_{約}, S_{[\delta_\omega]})$ を得る. たとえば, $\omega=55$℃として,次を得る.
| $(d):$ | 同時測定 ${\mathsf M}_{\overline{\mathcal A}}({\mathsf O}_{冷熱} \times {\mathsf O}_{約}, S_{[\delta_{55}]})$ により, \begin{align} & \text{測定値} \left[\begin{array}{c} (\text{冷}, \text{約50℃}) \\ (\text{冷}, \text{約60℃}) \\ (\text{熱}, \text{約50℃}) \\ (\text{熱}, \text{約60℃}) \end{array}\right] \text{を得る確率は} \left[\begin{array}{ll} 0.125 \\ 0.125 \\ 0.375 \\ 0.375 \end{array}\right] である \\ & \tag{3.12} \end{align} |
| $\fbox{注釈3.4}$ | 上記の議論は, 古典測定理論ならばいつも可能であるが,一般性は期待できない. 量子測定理論では, 2つの観測量を合わせて一つで済ますことができない 場合 (すなわち, 同時観測量${\mathsf O}_1\times {\mathsf O}_2$ が存在しない場合 )が頻繁に起こる, 次にその例をしめす. (4.3節のハイゼンベルグの不確定性原理参照). |
例 3.14[量子スピンの同時測定の非存在] 電子$P$のスピン状態は$\rho=|u \rangle \langle u|$ $\in$ ${\frak S}^p(B({\mathbb C}^2))$は, \begin{align*} u= \left[\begin{array}{ll} \alpha_1 \\ \alpha_2 \end{array}\right] \quad (\mbox{ここに, }|u|= (|\alpha_1|^2+ |\alpha_2|^2)^{1/2}=1) \end{align*} と表現できた. 電子$P$の$z$-軸方向のスピン観測量の測定 ${\mathsf M_{B({\mathbb C}^2)}}({\mathsf O}_z =(X,2^X, F^z ), S_{[\rho]})$を考える. ここに, ${\mathsf O}_z =(X,2^X, F^z )$ は次のように定まる: \begin{align*} F^z( \{ \uparrow \}) = \left[\begin{array}{ll} 1 & 0 \\ 0 & 0 \end{array}\right] , \quad F^z( \{ \downarrow \}) = \left[\begin{array}{ll} 0 & 0 \\ 0 & 1 \end{array}\right] \end{align*} さらに, 電子$P$の$x$-軸方向のスピン観測量の測定 ${\mathsf M_{B({\mathbb C}^2)}}({\mathsf O}_x =(X,2^X, F^x ), S_{[\rho]})$を考える. ここに, 「電子の$x$-軸方向のスピン」の観測量 ${\mathsf O}_x =(X,2^X, F^x )$ は次のように定まる: \begin{align*} F^x( \{ \uparrow \}) = \left[\begin{array}{ll} 1/2 & 1/2 \\ 1/2 & 1/2 \end{array}\right] , \quad F^x( \{ \downarrow \}) = \left[\begin{array}{ll} 1/2 & -1/2 \\ -1/2 & 1/2 \end{array}\right] \end{align*} さて, 問題は次である.
| $(a):$ | 二つの測定 ${\mathsf M_{B({\mathbb C}^2)}}({\mathsf O}_z =(X,2^X, F^z ), S_{[\rho ]})$ と ${\mathsf M_{B({\mathbb C}^2)}}({\mathsf O}_x =(X,2^X, F^x ), S_{[\rho ]})$とを同時に行えるか? |
実は, これは不可能である. なぜならば, 二つの観測量${\mathsf O}_z$と${\mathsf O}_x$が非可換だからである. たとえば,
\begin{align*} F^z( \{ \uparrow \})F^x( \{ \uparrow \}) = \left[\begin{array}{ll} 1 & 0 \\ 0 & 0 \end{array}\right] \cdot \left[\begin{array}{ll} 1/2 & 1/2 \\ 1/2 & 1/2 \end{array}\right] = \left[\begin{array}{ll} 1/2 & 1/2 \\ 0 & 0 \end{array}\right] \end{align*} \begin{align*} F^x( \{ \uparrow \})F^z( \{ \uparrow \}) = \left[\begin{array}{ll} 1/2 & 1/2 \\ 1/2 & 1/2 \end{array}\right] \cdot \left[\begin{array}{ll} 1 & 0 \\ 0 & 0 \end{array}\right] = \left[\begin{array}{ll} 1/2 & 0 \\ 1/2 & 0 \end{array}\right] \end{align*} となって, \begin{align*} F^x( \{ \uparrow \})F^z( \{ \uparrow \}) \not= F^z( \{ \uparrow \})F^x( \{ \uparrow \}) \end{align*} だからである.電子$P$のスピン状態は$\rho=|u \rangle \langle u|$ $\in$ ${\frak S}^p(B({\mathbb C}^2))$は,
\begin{align} u= \left[\begin{array}{l} \alpha_1 \\ \alpha_2 \end{array}\right] \quad (\mbox{where, }|u|= (|\alpha_1|^2+ |\alpha_2|^2)^{1/2}=1) \end{align}と表現できた. 電子$P$の$z$-軸方向のスピン観測量の測定 ${\mathsf M_{B({\mathbb C}^2)}}({\mathsf O}_z =(X,2^X, F^z ), S_{[\rho]})$を考える. ここに, ${\mathsf O}_z =(X,2^X, F^z )$ は次のように定まる:
\begin{align} F^z( \{ \uparrow \}) = \left[\begin{array}{ll} 1 & 0 \\ 0 & 0 \end{array}\right] , \quad F^z( \{ \downarrow \}) = \left[\begin{array}{ll} 0 & 0 \\ 0 & 1 \end{array}\right] \end{align}さらに, 電子$P$の$x$-軸方向のスピン観測量の測定 ${\mathsf M_{B({\mathbb C}^2)}}({\mathsf O}_x =(X,2^X, F^x ), S_{[\rho]})$を考える. ここに, 「電子の$x$-軸方向のスピン」の観測量 ${\mathsf O}_x =(X,2^X, F^x )$ は次のように定まる:
\begin{align} F^x( \{ \uparrow \}) = \left[\begin{array}{ll} 1/2 & 1/2 \\ 1/2 & 1/2 \end{array}\right] , \quad F^x( \{ \downarrow \}) = \left[\begin{array}{ll} 1/2 & -1/2 \\ -1/2 & 1/2 \end{array}\right] \end{align}
測定 ${\mathsf M_{B({\mathbb C}^2)}}({\mathsf O}_x =(X,2^X, F^x ), S_{[\rho]})$を得る。
さて, 問題は次である.
| $(a):$ | 二つの測定 ${\mathsf M_{B({\mathbb C}^2)}}({\mathsf O}_z =(X,2^X, F^z ), S_{[\rho ]})$ と ${\mathsf M_{B({\mathbb C}^2)}}({\mathsf O}_x =(X,2^X, F^x ), S_{[\rho ]})$とを同時に行えるか? |
実は, これは不可能である. なぜならば, 二つの観測量${\mathsf O}_z$と${\mathsf O}_x$が非可換だからである. たとえば,
\begin{align} F^z( \{ \uparrow \})F^x( \{ \uparrow \}) = \left[\begin{array}{lL} 1 & 0 \\ 0 & 0 \end{array}\right] \cdot \left[\begin{array}{ll} 1/2 & 1/2 \\ 1/2 & 1/2 \end{array}\right] = \left[\begin{array}{ll} 1/2 & 1/2 \\ 0 & 0 \end{array}\right] \end{align} \begin{align} F^x( \{ \uparrow \})F^z( \{ \uparrow \}) = \left[\begin{array}{ll} 1/2 & 1/2 \\ 1/2 & 1/2 \end{array}\right] \cdot \left[\begin{array}{ll} 1 & 0 \\ 0 & 0 \end{array}\right] = \left[\begin{array}{ll} 1/2 & 0 \\ 1/2 & 0 \end{array}\right] \end{align} となって, \begin{align} F^x( \{ \uparrow \})F^z( \{ \uparrow \}) \not= F^z( \{ \uparrow \})F^x( \{ \uparrow \}) \end{align} だからである. 次の定理は自明と思うが,念の為に証明も付けておく.定理 3.15 [精密測定とシステム量] $L^\infty(\Omega,\nu)$ 内の精密観測量 ${\mathsf O}^{(e)}_0=(X,{\cal F}, F^{\rm (exa)})$, すなわち, $(X,{\cal F}, F^{\rm (exa)})=(\Omega,{\cal B}_{\Omega}, \chi )$ を考える. また, システム量${\widetilde g}:\Omega \to {\mathbb R}$ の観測量表示を ${\mathsf O}_1=({\mathbb R},{\cal B}_{\mathbb R}, G)$ とする. 同時観測量 ${\mathsf O}^{(e)}_0 {{{\times}}} {\mathsf O}_1 $ の測定 ${\mathsf M}_{L^\infty (\Omega, \nu)}( {\mathsf O}^{(e)}_0{{{\times}}} {\mathsf O}_1 , S_{[\delta_\omega]} )$を考え, その測定値を $(x,y)$ $(\in X \times {\mathbb R})$とする. このとき, 確率$1$で, $x=\omega$ かつ $y= {\widetilde g}(\omega)$ が成立する.
証明
$\omega (\in \Omega
{{=}}
X )$
を含む任意の開集合を
$D_0
(\in {\cal B}_{\Omega} )$とする.
また,
${\widetilde g}(\omega)$
を含む任意の開集合を$D_1 (\in {\cal B}_{\mathbb R})$
とする.
${\mathsf M}_{L^\infty (\Omega, \nu)}(
{\mathsf O}^{(e)}_0
{{{\times}}}
{\mathsf O}_1
, S_{[\delta_\omega]} )$
の測定値$(x,y)$が$D_0 \times D_1$
に含まれる確率は,
$\chi_{_{D_0}}(\omega) \cdot \chi_{_{{\widetilde g}^{-1}(D_1)}} (\omega )=1$.
よって,
$D_0$と$D_1$
の任意性より,確率$1$で,
$x=\omega$
かつ
$y={\widetilde g}(\omega)$
を得る.