3.3.2: 「状態は動かない」と擬積観測量
言語的解釈の肝は,
「測定は一回だけ」で,したがって,「状態は動かない」
が要請される.なぜならば,
からである.
したがって、量子言語では、
$(a):$
「状態が動いたかどうか?」は,(前後で)二回測定をしないとわからないのだから,
その確認は不可能である


次の復習から始める:
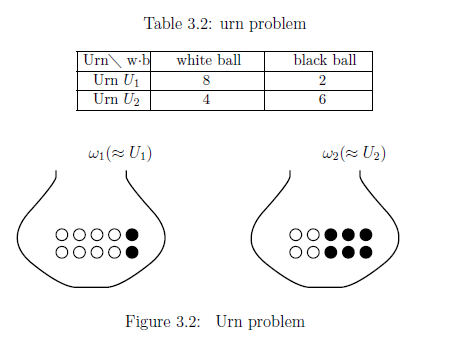
復習3.16 [= 例 2.34 (in $\S$2.8)] 2つの壷 ${U}_1$, ${U}_2$ がある. 壷 ${U}_1$には8個の白球と2個の黒球, 壷 ${U}_2$には4個の白球と6個の黒球 が入っているとする.
| $(a):$ | 壷 $U_2$から1つの球を取り出すとき, その球が $ \left[\begin{array}{ll} 白 \\ 黒 \end{array}\right] $ である確率は $ \left[\begin{array}{ll} 0.4 \\ 0.6 \end{array}\right] $ である. |
ここで,この日常言語の文言(a)を測定理論 の 言葉遣いで記述することを考える. $\Omega = \{ {\omega}_1 , {\omega}_2 \}$ として, 離散距離空間$(\Omega, d_D)$を考えて, 可換$C^*$代数$C_0(\Omega)$を得る. したがって, \begin{align*} \mbox{ 古典系の基本構造 $[C_0(\Omega ) \subseteq L^\infty (\Omega, \nu ) \subseteq B(L^2 (\Omega, \nu ))]$ } \end{align*} を考えよう. 純粋状態空間は
\begin{align*} {\frak S}^p (C_0(\Omega)^*)= \{ \delta_{\omega_1} , \delta_{\omega_2} \} \end{align*} となる. ここで, , \begin{align*} U_1 \quad \cdots \quad \text{"状態$\delta_{\omega_1}$をもつ壷"}, \qquad U_2 \quad \cdots \quad \text{"状態$\delta_{\omega_2}$をもつ壷"} \end{align*} として, 次の同一視を考える (したがって,図3.2のような状況を考える): \begin{align*} U_1 \approx \delta_{\omega_1} \approx \omega_1 , \qquad U_2 \approx \delta_{\omega_2} \approx \omega_2 \quad \quad \end{align*}更に, $L^\infty (\Omega{})$内の観測量 ${\mathsf O}_{白黒} = ( \{ 白, 黒 \}, 2^{\{ 白, 黒 \} } , F_{白黒}{})$ を次のように定義する:
\begin{align} & [F_{白黒}(\{ 白 \}{})](\omega_1{})= 0.8, & \quad & [ F_{白黒}(\{ 黒 \}{})](\omega_1{})= 0.2 \nonumber \\ & [F_{白黒}(\{ 白 \}{})](\omega_2{})= 0.4, & \quad & [F_{白黒}(\{ 黒 \}{})] (\omega_2{})= 0.6 \label{eq3.13} \end{align}このようにして, 測定 ${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{白黒} , S_{ [{}{\delta_{\omega_2}}]}{})$ を得る. よって,上述の(a)は, 測定理論(=量子言語)の言葉で次のように翻訳できる:
| $(b):$ |
測定
${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{白黒} ,
S_{ [{}{\omega_2}]}{})$
により,
測定値
$
\left[\begin{array}{ll}
白
\\
黒
\end{array}\right]
$
が得られる確率は
$ \left[\begin{array}{l} \int_\Omega [F_{白黒}(\{白\})](\omega) \delta_{\omega_2}(d \omega ) = [F_{白黒}(\{白\})](\omega_2)= 0.4 \quad \\ \int_\Omega [F_{白黒}(\{黒\})](\omega) \delta_{\omega_2}(d \omega ) = {[F_{白黒}(\{黒 \})]} (\omega_2)= 0.6 \quad \end{array}\right] $ である. |
| $(a):$ | [復元抽出(=同時測定)]: 壷 $U_2$から1つの球を取り出して,それの「白・黒」を確認して, その球をまた壷 $U_2$に戻して,よくかき混ぜてから,もう一度,壷 $U_2$から1つの球を取り出す. したがって,可能性としては,4つの \begin{align*} (白,白)\;\;(白,黒)\;\;(黒,白)\;\;(黒,黒)\;\; \end{align*} である. 簡単な計算で, $ \left[\begin{array}{l} (白,白) \quad \\ (白,黒) \\ (黒,白) \\ (黒,黒) \end{array}\right] $ である確率は $ \left[\begin{array}{c} 0.16 \\ 0.24 \\ 0.24 \\ 0.36 \\ \end{array}\right] $ であることがわかる. |
解答
解答
$\;\;\;$
測定
${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{白黒} ,
S_{ [{}{\delta_{\omega_2}}]}{})$
の同時測定${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{白黒} {{{\times}}} {\mathsf O}_{白黒} ,
S_{ [{}{\delta_{\omega_2}}]}{})$
を考えればよい.
このとき,
$L^\infty (\Omega{})$内の同時観測量
${\mathsf O}_{白黒}^2 = ( \{ 白, 黒 \}\times
\{ 白, 黒 \}
, 2^{\{ 白, 黒 \} \times \{ 白, 黒 \} } ,$
$ F_{白黒}^2{}(=
F_{白黒}
\times
F_{白黒}
)
)$
は,つぎのように定まる.
\begin{align*}
& F_{白黒}^2(\{ (白, 白) \}{})(\omega_1{})= 0.64,
& \quad & F^2(\{ (白,黒) \}{})(\omega_1{})= 0.16
\\
& F_{白黒}^2(\{ (黒,白) \}{})(\omega_1{})= 0.16,
& \quad & F^2(\{ (黒,黒) \}{})(\omega_1{})= 0.4
\\
& F_{白黒}^2(\{ (白, 白) \}{})(\omega_2{})= 0.16,
& \quad & F^2(\{ (白,黒) \}{})(\omega_2{})= 0.24
\\
& F_{白黒}^2(\{ (黒,白) \}{})(\omega_2{})= 0.24,
& \quad & F^2(\{ (黒,黒) \}{})(\omega_2{})= 0.36
\end{align*}
このようにして,
同時測定
${\mathsf M}_{C(\Omega)} ({\mathsf O}_{白黒}^2,
S_{ [{}{\omega}]}{})$
を得る.
よって,上述の(a)は,
測定理論の言葉で次のように翻訳できる:
| $(b):$ |
同時測定${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{白黒} {{{\times}}} {\mathsf O}_{白黒} ,
S_{ [{}{\delta_{\omega_2}}]}{})$
により得られた
測定値
$
\left[\begin{array}{c}
(白,白) \quad
\\
(白,黒)
\\
(黒,白)
\\
(黒,黒)
\end{array}\right]
$
である確率は
$ \left[\begin{array}{c} {[F_{白黒}(\{白\})](\omega_2) \cdot [F_{白黒}(\{白\})](\omega_2)=0.16} \quad \\ {[F_{白黒}(\{白\})](\omega_2) \cdot [F_{白黒}(\{黒\})](\omega_2)=0.24} \\ {[F_{白黒}(\{黒\})](\omega_2) \cdot [F_{白黒}(\{白\})](\omega_2)=0.24} \\ {[F_{白黒}(\{黒\})](\omega_2) \cdot [F_{白黒}(\{黒\})](\omega_2)=0.36} \end{array}\right] $ である. |
| $(a):$ | [非復元抽出]:壷 $U_2$から1つの球を取り出して,それの「白 or 黒」を確認して, \begin{align*} \text{ その球を壷 $U_2$に戻さないで, } \end{align*} もう一度,壷 $U_2$から1つの球を取り出す. |
これを測定理論の言葉で表現するには,どうしたらよいか? これを 解答3.20で答える.
さて,
同時観測量
(定義3.12(in $\S$3.3)
を思い出そう.
各
$k = 1,2,\ldots, n$
に対して,
基本代数${\mathcal A}$
内の
観測量 ${\mathsf O}_k$
${{=}}$
$(X_k , $
${\cal F}_k , $
$F_k{})$を
考えて,
同時観測量
$\widehat{\mathsf O}$
${{=}}$
$({{{\times}}}_{k=1}^n X_k ,$
$ \boxtimes_{k=1}^n{\cal F}_k , $
$\widehat{F}{})$
を次のように定義した:
\begin{align*}
{\widehat
F}(\Xi_1 \times \Xi_2 \times \cdots \times \Xi_n{})
=
F_1 (\Xi_1{}) F_2 (\Xi_2{}) \cdots F_n (\Xi_n{})
\\
(\forall \Xi_k \in {\cal F}_k , \forall k =1,2,\ldots,n )
\end{align*}
次の定義は同時観測量
の
一般化である
定義 3.19 [擬積観測量(quasi-product observable ) ] 各 $k = 1,2,\ldots, n$ に対して, 基本代数${\mathcal A}$ 内の 観測量 ${\mathsf O}_k$ ${{=}}$ $(X_k , $ ${\cal F}_k , $ $F_k{})$ 考える. 観測量 ${\mathsf O}_{12...n}$ ${{=}}$ $({{{\times}}}_{k=1}^n X_k ,$ $ \boxtimes_{k=1}^n{\cal F}_k , $ ${F}_{12...n}{})$ は次を満たすとする: \begin{align} & {F}_{12...n}(X_1 \times \cdots \times X_{k-1} \times \Xi_k \times X_{k+1} \times \cdots \times X_n ) = F_k (\Xi_k{}) \label{eq3.14} \\ & \quad \qquad \qquad (\forall \Xi_k \in {\cal F}_k , \forall k =1,2,\ldots,n ) \nonumber \end{align} このとき, 観測量 ${\mathsf O}_{12...n}$ ${{=}}$ $({{{\times}}}_{k=1}^n X_k ,$ $ \boxtimes_{k=1}^n{\cal F}_k , $ ${F}_{12...n}{})$ は $\{ {\mathsf O}_k \; | \;k=1,2,\ldots,n \}$ の 擬積観測量 と呼ばれ, 次のように記される: \begin{align*} \mathop{{{{\times}}}}^{qp}_{k=1,2,\ldots,n }{\mathsf O}_k = ({{{\times}}}_{k=1}^n X_k , \boxtimes_{k=1}^n{\cal F}_k, {\mathop{{{{\times}}}}^{qp}_{k=1,2,\ldots,n} }F_k{}) \end{align*} もちろん, 同時観測量も 擬積観測量の一種で, したがって, 擬積観測量は,一般には 一意に決まらない. また,$C^*$代数${\mathcal A}$が可換でない場合は,存在も保証されているわけではない.
解答 3.20 [ 問題3.18の解答] $\;\;$ $L^\infty (\Omega{})$ 内の観測量 ${\mathsf O}_{白黒} = ( \{ 白, 黒 \}, 2^{\{ 白, 黒 \} } , F{})$ の擬積観測量 $ {\mathsf O}_{白黒} \mathop{{{{\times}}}}^{qp} {\mathsf O}_{白黒} = ( \{ 白, 黒 \} \times \{ 白, 黒 \} , 2^{\{ 白, 黒 \} \times \{ 白, 黒 \} } ,$ $ F_{12}(= F_{白黒} \mathop{{{{\times}}}}^{qp} F_{白黒} ))$ を次のように定める: \begin{align*} & F_{12}(\{ (白, 白) \}{})(\omega_1{})= \frac{8 \times 7}{90}, & \quad & F_{12}(\{ (白,黒) \}{})(\omega_1{})= \frac{8 \times 2}{90} \\ & F_{12}(\{ (黒,白) \}{})(\omega_1{})= \frac{2 \times 8}{90}, & \quad & F_{12}(\{ (黒,黒) \}{})(\omega_1{})= \frac{2 \times 1}{90} \\ & F_{12}(\{ (白, 白) \}{})(\omega_2{})= \frac{4 \times 3}{90}, & \quad & F_{12}(\{ (白,黒) \}{})(\omega_2{})= \frac{4 \times 6}{90} \\ & F_{12}(\{ (黒,白) \}{})(\omega_2{})= \frac{6 \times 4}{90}, & \quad & F_{12}(\{ (黒,黒) \}{})(\omega_2{})= \frac{6 \times 5}{90} \end{align*} このようにして, 測定 ${\mathsf M}_{C(\Omega)} ({\mathsf O}_{12}, S_{ [{}{\omega}]}{})$ を得る. したがって,測定理論の言葉で次のように記述できる:
| $(b):$ |
擬積観測量の測定${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{白黒} \mathop{{{{\times}}}}^{qp} {\mathsf O}_{白黒} ,
S_{ [{}{\delta_{\omega_2}}]}{})$
により得られた
測定値が
$
\left[\begin{array}{l}
(白,白) \quad
\\
(白,黒)
\\
(黒,白)
\\
(黒,黒)
\end{array}\right]
$
である確率は $ \left[\begin{array}{l} {[F_{12}(\{ (白, 白) \})](\omega_2) =\frac{4 \times 3}{90} } \quad \\ \\ { [F_{12}(\{(白, 黒)\})](\omega_2) =\frac{4 \times 6}{90} } \\ \\ { [ F_{12}(\{ (黒, 白) \})](\omega_2) =\frac{4 \times 6}{90} } \\ \\ { [F_{12}(\{(黒, 黒) \}{})](\omega_2) =\frac{6 \times 5}{90} } \end{array}\right] $ である. |