さて,今度は,
次のような測定を考えよう:
定義3.22 [ 並行観測量]
各
$k = 1,2,\ldots,n$
に対して,
基本構造
$[C_0(\Omega_k) \subseteq L^\infty (\Omega_k ) \subseteq
B(L^2 (\Omega_k, \nu_k ))]$内の
観測量 ${\mathsf O}_k$
$=$
$(X_k , {\cal F}_k , F_k{})$
考える.
$({{{\times}}}_{k=1}^n X_k ,$
$ \boxtimes_{k=1}^n{\mathcal F}_k)$
を直積可測空間とする.
$
L^\infty ({{{\times}}}_{k=1}^n \Omega_k )
$
内の
観測量
$\widetilde{\mathsf O}=
(
{{{{\times}}}_{k=1}^n X_k }, \boxtimes_{k=1}^n {\cal F}_k , \widetilde{F}{})$
を次を満たすように定める:
\begin{align}
&
[{\widetilde F}(\Xi_1 \times \Xi_2 \times \cdots \times \Xi_n{})]
(\omega_1, \omega_2, \cdots, \omega_n )
\nonumber
\\
=
&
[F_1 (\Xi_1{})]
(\omega_1)
\otimes
[F_2 (\Xi_2{})]
(\omega_2)
\otimes
\cdots
\otimes
[F_n (\Xi_n{})]
(\omega_n )
\label{eq3.15}
\\
&
\qquad
\qquad
\forall
(\omega_1, \omega_2,\ldots, \omega_n )\in
{\widetilde \Omega} =
{{{\times}}}_{k=1}^n \Omega_k,
\;\;
\forall \Xi_k \in {\cal F}_k \;
(k=1,2,\ldots,n )
\nonumber
\end{align}
このとき,
この観測量$\widetilde{\mathsf O}$
$=$
$({{{\times}}}_{k=1}^n X_k , \boxtimes_{k=1}^n{\cal F}_k , \widetilde{F}{})$
を,
$\{{\mathsf O}_k \}_{k=1}^n$
の
$
L^\infty ({{{\times}}}_{k=1}^n \Omega_k )
$
内の
{\bf 並行観測量}
と呼び,
${\widetilde F}=\bigotimes_{k=1}^n F_k$,
$\widetilde{\mathsf O}$
$=$
$\bigotimes_{k=1}^n
{\mathsf O}_k
$
と記す.
並行観測量
${\widetilde{\mathsf O}}=$
$\bigotimes_{k=1}^n {\mathsf O}_k$
の測定,
すなわち,
${\mathsf M}_{
L^\infty ({{{\times}}}_{k=1}^n \Omega_k )
}
$
$
(\widetilde{\mathsf O}, $
$S_{
[
(\omega_1, \omega_2, \cdots, \omega_n )
]
})$
を
並行測定
と呼び,
${\mathsf M}_{L^\infty (
\times_{k=1}^n
\Omega_k)} (
\bigotimes_{k=1}^n {\mathsf O}_k,$
$ S_{[
\bigotimes_{k=1}^n
\delta_{\omega_k}]})$
とか
$\bigotimes_{k=1}^n {\mathsf M}_{L^\infty (\Omega_k )} ({\mathsf O}_k,$
$S_{[
\omega_k]})$
とも書く.
並行測定の意味は次のようである。
注意3.24また,
たとえば,
$(\omega_1,\omega_2 ) =(55, 55)$として,次を得る:
だからである.
$\;\;\;\;$
これは,
例3.13と同じ結果であることに注意せよ
(後出の注釈3.5参照).
次の定理の証明は自明であるが,その意味は深い.
定理 3.25 [エルゴード性]
各$k=1,2, \cdots, n$に対して,
${\mathsf M}_{L^\infty (
\Omega)} ( {\mathsf O}_k(:=(X_k,{\mathcal F}_k, F_k)), S_{[\delta_\omega]})$
はサンプル空間
$(X_k,{\mathcal F}_k, P_k^{\omega})$を持つとする.
このとき,
同時測定
${\mathsf M}_{L^\infty (
\Omega)} ({{{\times}}}_{k=1}^n {\mathsf O}_k, S_{[\delta_\omega]})$
のサンプル確率空間
と
並行測定
${\mathsf M}_{L^\infty (
\Omega^n)}$
$ (
\bigotimes_{k=1}^n {\mathsf O}_k
, $
$S_{[
\otimes_{k=1}^n \delta_{\omega}]})$
のサンプル確率空間
は等しくて,直積確率空間
\begin{align}
({{{\times}}}_{k=1}^n X_k,\boxtimes_{k=1}^n{\mathcal F}_k,\bigotimes_{k=1}^n P_k^{\omega})
\label{eq3.17}
\end{align}
となる.
証明
$\;\;$容易なので省く.
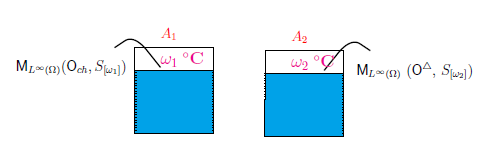
$(a):$ 2つのコップAとBの中に,水{(}お湯)が入っている.
コップAの水の
温度は$\omega_1$℃,
コップBの水の
温度は$\omega_2$℃
とする(温度が同じとは限らない).
「コップAの水が冷たいか?熱いか?」
を調べて,
しかも
「コップBの水が約何℃か」を測定することを
考えたい.
これは
\begin{align*}
\text{状態空間}\Omega_1 = [0,100],
\qquad
\text{状態空間}\Omega_2 = [0,100]
\end{align*}
として,
例2.31
の
測定
${\mathsf M}_{C ( \Omega_1 )} ( {\mathsf O}_{冷熱}
{{=}}
(\{冷,熱\},
2^{\{冷,熱\}}, F_{冷熱} ), S_{[\delta_{\omega_1}]} )$
と
例2.32
の
測定
${\mathsf M}_{C ( \Omega_2 )}$
$ ({\mathsf O}_{約}{{=}}$
$
({\mathbb N}_{10}^{100} , $
$
2^{{\mathbb N}_{10}^{100} }, G_{約} ),
S_{[\omega_2]} )
$
の2つの測定を
行うことと同じである
$\quad$ $
\left\{\begin{array}{ll}
\mbox{
$(\sharp_1)$:
${\mathsf M}_{L^\infty ( \Omega )} ( {\mathsf O}_{{{{{c}}}}{{{{h}}}}}
{{=}}
(\{{{{{c}}}},{{{{h}}}}\}
, 2^{\{{{{{c}}}},{{{{h}}}}\}}, F_{{{{{c}}}}{{{{h}}}}} ), S_{[\omega_1]} )$
in 例 2.31}
\\
\\
\mbox{
$(\sharp_2)$
:
${\mathsf M}_{L^\infty ( \Omega )}$
$ ({\mathsf O}^{\triangle}
$
$
{{=}}
({\mathbb N}_{10}^{100} ,$
$
2^{{\mathbb N}_{10}^{100} }, G_{約} ),$
$
S_{[\omega_2]} )
$
in
例2.32
}
\end{array}\right.
$
しかしながら, 上で述べたように,
\begin{align}
\mbox{
「状態は一つだけ」
}
\end{align}
ここで、次の問題を得る.

以下にこれを考える.
であった.
すなわち
$\quad$
測定
${\mathsf M}_{L^\infty (\Omega_1) }({\mathsf O}_1, S_{[\omega_1]})$
と
測定
${\mathsf M}_{L^\infty (\Omega_2 )}({\mathsf O}_2, S_{[\omega_2]})$
の2つの測定を行いたい.
しかしながら, 言語的解釈 ($\S$3.1)は二つの測定を禁じている。よって,
$(b):$ $ \left\{\begin{array}{ll}
\overset{{}}{\underset{ \rho_1 (\in {\frak S}^p({\mathcal A}_1^*) )}
{{ \fbox{状態}}}}
\xrightarrow[]{\qquad \qquad}
\overset{{}}
{
\underset{ {\mathsf O}_1}
{{ \fbox観測量}}
}
\xrightarrow[{\mathsf M}_{\overline{\mathcal A}_1 }({\mathsf O}_1, S_{[{\rho_1}]})]{\qquad \qquad}
\overset{{}}
{
\underset{ x_1 (\in X_1 )}
{{ \fbox{測定値}}}
}
\\
\\
\overset{{}}{\underset{ \rho_2 (\in {\frak S}^p({\mathcal A}_2^*))}
{{ \fbox{状態}}}}
\xrightarrow[]{\qquad \qquad}
\overset{{}}
{
\underset{ {\mathsf O}_2}
{{ \fbox観測量}}
}
\xrightarrow[{\mathsf M}_{\overline{\mathcal A}_2}({\mathsf O}_2, S_{[{\rho_2}]})]{\qquad \qquad}
\overset{{}}
{
\underset{ x_2 (\in X_2 )}
{{ \fbox{測定値}}}
}
\end{array}\right.
$
そうならば、
2つの状態
$
\omega_1 (\in \Omega_1)
$
と
$
\omega_2 (\in \Omega_2)
$
を一つの状態
$(\omega_1, \omega_2 ) (\in \Omega_1 \times \Omega_2)$
と見なして,
更に,
2つの観測量${\mathsf O}_1$と${\mathsf O}_2$を
合わせて,
並行観測量
${\mathsf O}_1 \otimes {\mathsf O}_2$
を構成して,
並行測定
${\mathsf M}_{L^\infty ( \Omega_1 \times \Omega_2) }({\mathsf O}_1 \otimes
{\mathsf O}_2
, S_{[
(\omega_1, \omega_2 )]})$
を行えばよい.
これを図示すると,
$(c):$
$ \overset{{}}{\underset{
\rho_1 \otimes \rho_2 (\in {\frak S}^p({\mathcal A}_1^*)
\otimes
{\frak S}^p({\mathcal A}_2^*)
)
}
{{ \fbox{state}}}}
\xrightarrow[]
{
\underset{ {\mathsf O}_1 \otimes {\mathsf O}_2}
{{ \fbox{parallel 観測量}}}
}
\xrightarrow[
{\mathsf M}_{
\overline{\mathcal A}_1
\otimes
\overline{\mathcal A}_2
}({\mathsf O}_1 \otimes
{\mathsf O}_2
, S_{[
\rho_1 \otimes \rho_2
]})]
{\qquad \qquad}
{
\underset{ (x_1,x_2) (\in X_1 \times X_2 )}
{{ \fbox{測定値}}}
}
$
 例 3.23 [問題3.21の解答]
2つの状態空間
$\Omega_1( \approx {\frak S}^p(C_0(\Omega_1)^*))$
と
$\Omega_2( \approx {\frak S}^p(C_0(\Omega_2)^*))$
を
閉区間
$\Omega_1 = \Omega_2 = [0,100]$
と定める.
$L^\infty(\Omega_1)$内の観測量を
例2.31
の
冷熱-観測量
${\mathsf O}_{冷熱}=$
$ (X ({{=}} \{ 冷 , 熱 \}), 2^X,$
$ F_{冷熱} )$
として,
$L^\infty(\Omega_2)$内の観測量を
例2.32の
約-観測量
${\mathsf O}_{約}=$
$ (Y( {{=}} {\mathbb N}_{10}^{100}) ,$
$2^Y, G_{約} )$
とする.
したがって,
$L^\infty(\Omega_1 \times \Omega_2 )$内の
並行観測量
${\mathsf O}_{冷熱} \otimes {\mathsf O}_{約}$
$=$
$(\{ 冷 , 熱 \}\times {\mathbb N}_{10}^{100},$
$
2^{\{ 冷 , 熱 \}\times {\mathbb N}_{10}^{100}},
$
$
F_{冷熱} \otimes G_{約} )$
を定めて,
並行測定
${\mathsf M}_{L^\infty(\Omega_1 \times \Omega_2 )}({\mathsf O}_{冷熱} \otimes {\mathsf O}_{約},
S_{[\delta_{(\omega_1,\omega_2)}]})$
を考える.
たとえば,
$(\omega_1,\omega_2 ) =(25, 55)$として,次を得る:
例 3.23 [問題3.21の解答]
2つの状態空間
$\Omega_1( \approx {\frak S}^p(C_0(\Omega_1)^*))$
と
$\Omega_2( \approx {\frak S}^p(C_0(\Omega_2)^*))$
を
閉区間
$\Omega_1 = \Omega_2 = [0,100]$
と定める.
$L^\infty(\Omega_1)$内の観測量を
例2.31
の
冷熱-観測量
${\mathsf O}_{冷熱}=$
$ (X ({{=}} \{ 冷 , 熱 \}), 2^X,$
$ F_{冷熱} )$
として,
$L^\infty(\Omega_2)$内の観測量を
例2.32の
約-観測量
${\mathsf O}_{約}=$
$ (Y( {{=}} {\mathbb N}_{10}^{100}) ,$
$2^Y, G_{約} )$
とする.
したがって,
$L^\infty(\Omega_1 \times \Omega_2 )$内の
並行観測量
${\mathsf O}_{冷熱} \otimes {\mathsf O}_{約}$
$=$
$(\{ 冷 , 熱 \}\times {\mathbb N}_{10}^{100},$
$
2^{\{ 冷 , 熱 \}\times {\mathbb N}_{10}^{100}},
$
$
F_{冷熱} \otimes G_{約} )$
を定めて,
並行測定
${\mathsf M}_{L^\infty(\Omega_1 \times \Omega_2 )}({\mathsf O}_{冷熱} \otimes {\mathsf O}_{約},
S_{[\delta_{(\omega_1,\omega_2)}]})$
を考える.
たとえば,
$(\omega_1,\omega_2 ) =(25, 55)$として,次を得る:
なぜならば、
\begin{align}
&
[(F_{{{{{c}}}}{{{{h}}}}} \otimes G_{約})(
\{ (\mbox{c},
\mbox{about 50°C}
) \}
)]
(25,55)
\\
=
&
[F_{{{{{c}}}}{{{{h}}}}}(\{ \mbox{c} \} )](25)
\cdot [G_{約}(\{ \mbox{about 50°C}\})](55)
=0.75 \cdot 0.5=0.375
\end{align}
同様に、
\begin{align}
&
[(F_{{{{{c}}}}{{{{h}}}}} \otimes G_{約})(
\{ (\mbox{c},
\mbox{about 60°C}
) \}
)]
(25,55)
=0.75 \cdot 0.5=0.375
\\
&
[(F_{{{{{c}}}}{{{{h}}}}} \otimes G_{約})(
\{ (\mbox{h},
\mbox{about 50°C}
) \}
)]
(25,55)
=0.25 \cdot 0.5=0.125
\\
&
[(F_{{{{{c}}}}{{{{h}}}}} \otimes G_{約})(
\{ (\mbox{h},
\mbox{about 60°C}
) \}
)]
(25,55)
=0.25 \cdot 0.5=0.125
\end{align}
だからである。
$(d):$ 並行測定 ${\mathsf M}_{L^\infty (\Omega_1 \times \Omega_2 )}({\mathsf O}_{{{{{c}}}}{{{{h}}}}} \otimes {\mathsf O}^{\triangle}, S_{[(25,55)]})$を行ったとしよう。
\begin{align}
&
\mbox{that
}
\mbox{測定値 }
\left[\begin{array}{ll}
(\mbox{c}, \mbox{about 50°C})
\\
(\mbox{c}, \mbox{about 60°C})
\\
(\mbox{h}, \mbox{about 50°C})
\\
(\mbox{h}, \mbox{about 60°C})
\end{array}\right]
\mbox{が得られる確率は}
\left[\begin{array}{ll}
0.375
\\
0.375
\\
0.125
\\
0.125
\end{array}\right]
\end{align}
である。
なぜならば,同様に,
\begin{align}
\left\{\begin{array}{ll}
&
[F_{{{{{c}}}}{{{{h}}}}}(\{ \mbox{c} \} )](55)
\cdot [G_{約}(\{ \mbox{about 50°C}\})](55)
=0.25 \cdot 0.5=0.125
\\
&
[F_{{{{{c}}}}{{{{h}}}}}(\{ \mbox{c} \} )](55)
\cdot [G_{約}(\{ \mbox{about 60°C}\})](55)
=0.25 \cdot 0.5=0.125
\\
&
[F_{{{{{c}}}}{{{{h}}}}}(\{ \mbox{h} \} )](55)
\cdot [G_{約}(\{ \mbox{about 50°C}\})](55)
=0.75 \cdot 0.5=0.375
\\
&
[F_{{{{{c}}}}{{{{h}}}}}(\{ \mbox{h} \} )](55)
\cdot [G_{約}(\{ \mbox{about 60°C}\})](55)
=0.75 \cdot 0.5=0.375
\end{array}\right.
\\
&
\tag{3.16}
\end{align}
$(e):$ 並行測定
${\mathsf M}_{C(\Omega_1 \times \Omega_2 )}({\mathsf O}_{冷熱} \otimes {\mathsf O}_{約},
S_{[\delta_{(55,55)}]})$
により,
\begin{align*}
&
\text{測定値}
\left[\begin{array}{l}
(\text{冷}, \text{約50℃}) \quad
\\
(\text{冷}, \text{約60℃})
\\
(\text{熱}, \text{約50℃})
\\
(\text{熱}, \text{約60℃})
\end{array}\right]
\text{を得る確率は}
\left[\begin{array}{ll}
0.125
\\
0.125
\\
0.375
\\
0.375
\end{array}\right]
である.
\end{align*}
例 3.26 [量子スピンの並行測定] 電子$P$のスピン状態は$\rho=|u \rangle \langle u|$ $\in$ ${\frak S}^p(B({\mathbb C}^2))$は,
\begin{align} u_1= \left[\begin{array}{l} \alpha_1 \\ \beta_1 \end{array}\right] \quad (\mbox{where, }\|u_1 \|= (|\alpha_1|^2+ |\beta_1|^2)^{1/2}=1) \end{align}と表現できた. 電子$P$の$z$-軸方向のスピン観測量の測定 ${\mathsf M_{B({\mathbb C}^2)}}({\mathsf O}_z =(X,2^X, F^z ), S_{[\rho]})$を考える. ここに, ${\mathsf O}_z =(X,2^X, F^z )$ は次のように定まる:
\begin{align} F^z( \{ \uparrow \}) = \left[\begin{array}{ll} 1 & 0 \\ 0 & 0 \end{array}\right] , \quad F^z( \{ \downarrow \}) = \left[\begin{array}{ll} 0 & 0 \\ 0 & 1 \end{array}\right] \end{align}
測定${\mathsf M_{B({\mathbb C}^2)}}({\mathsf O}_z =(X,2^X, F^z ), S_{[\rho_1]})$を得る.
電子$P_2$のスピン状態は$\rho_2=|u_2 \rangle \langle u_2|$ $\in$ ${\frak S}^p(B({\mathbb C}^2))$
は次としよう:
${\mathsf O}_x =(X,2^X, F^x )$を$z$-軸方向のスピン観測量とする:
\begin{align} F^x( \{ \uparrow \}) = \left[\begin{array}{ll} 1/2 & 1/2 \\ 1/2 & 1/2 \end{array}\right] , \quad F^x( \{ \downarrow \}) = \left[\begin{array}{ll} 1/2 & -1/2 \\ -1/2 & 1/2 \end{array}\right] \end{align}
測定${\mathsf M_{B({\mathbb C}^2)}}({\mathsf O}_x =(X,2^X, F^x ), S_{[\rho_2]})$を得る。
よって、次の問題を得る。
| $(a):$ | 二つの測定${\mathsf M_{B({\mathbb C}^2)}}({\mathsf O}_z =(X,2^X, F^z ), S_{[\rho_1 ]})$と${\mathsf M_{B({\mathbb C}^2)}}({\mathsf O}_x =(X,2^X, F^x ), S_{[\rho_2 ]})$を一回の測定で済ますことができるか? |
| $(b):$ |
並行測定 ${\mathsf M_{B({\mathbb C}^2) \otimes B({\mathbb C}^2)}}({\mathsf O}_z \otimes {\mathsf O}_z, S_{[\rho \otimes \rho
]})$によって$
\mbox{測定値}
\left[\begin{array}{ll}
(
\uparrow,
\uparrow
)
\\
(
\uparrow,
\downarrow)
\\
(\downarrow,
\uparrow
)
\\
(\downarrow,
\downarrow)
\end{array}\right]
$が得られる確率は
$ \qquad \qquad \left[\begin{array}{ll} \langle u, F^z(\{\uparrow \})u \rangle \langle u, F^x(\{\uparrow \})u \rangle =p_1 p_2 \\ \langle u, F^z(\{\uparrow \})u \rangle \langle u, F^x(\{\downarrow \})u \rangle =p_1(1- p_2) \\ \langle u, F^z(\{\downarrow \})u \rangle \langle u, F^x(\{\uparrow \})u \rangle =(1-p_1) p_2 \\ \langle u, F^z(\{\downarrow \})u \rangle \langle u, F^x(\{\downarrow \})u \rangle =(1-p_1) (1- p_2) \end{array}\right] $ である。 ここで$ p_1=|\alpha_1|^2, \quad p_2=\frac{1}{2}(|\alpha_2|^2 +\overline{\beta}_2 \alpha_2 +\beta_2 \overline{\alpha}_2 + |\beta_2|^2) $ |
| $\fbox{注釈3.5}$ | この定理3.25定理は,以下の意味で意外と深い.
しかし, これ は, 純粋古典測定 の著しい特徴である. 混合古典測定(第9章)や量子測定では,同時測定と並行測定の違いが鮮明で, たとえば,量子測定においては, 同時測定は一般には存在するとは限らないが, 並行測定は必ず存在する. |
 たとえば,
「一つのサイコロを1000回投げること」は
同時測定で,「
1000個のサイコロを投げること」は並行測定
である.
それらの結果
─
すなわち,
サンプル確率空間
─
は同じになること(
たとえば,
「一つのサイコロを1000回投げること」は
同時測定で,「
1000個のサイコロを投げること」は並行測定
である.
それらの結果
─
すなわち,
サンプル確率空間
─
は同じになること(
