4.3.1: ハイゼンベルグの不確定性原理は疑わしい
まず、ハイゼンベルグの不確定性原理を述べておく。 命題4.10 [ハイゼンベルグの不確定性原理(1927)]| $\mbox{(i):}$ | 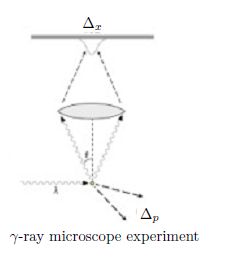 ある粒子の位置$x$は精密測定できる.また同様に,運動量$p$も精密測定できる.しかし,位置$x$と運動量$p$を共に精密測定することは不可能で,それぞれの誤差$\Delta x$と$\Delta p$が不可避な近似測定しかできない. ある粒子の位置$x$は精密測定できる.また同様に,運動量$p$も精密測定できる.しかし,位置$x$と運動量$p$を共に精密測定することは不可能で,それぞれの誤差$\Delta x$と$\Delta p$が不可避な近似測定しかできない. |
| $\mbox{(ii):}$ | そして,誤差$\Delta x$と$\Delta p$は,次の「ハイゼンベルグの不確定性関係」を満たす.すなわち,\begin{align}\Delta x\cdot \Delta p \; {\doteqdot}\; \hbar (=\text{プランク定数}/2\pi{\doteqdot}1.5547 \times 10^{-34} Js).\tag{4.20}\end{align}したがって,一方の精度を上げれば,必然的に,他方の精度は落ちる. |
これが、有名な「$\gamma$線顕微鏡による思考実験」によって、導出されたとされているハイゼンベルグの不確定性原理で、
| $(A):$ | 20世紀におけるもっとも有名な命題の一つ |
である。
しかしながら、この命題は次の意味で疑わしい。| $\fbox{注釈4.1}$ | 実は,ハイゼンベルグの不確定性原理(命題4.10)は意味不明な気分だけの文言(すなわち,日常言語の中に何となく埋没した数量表現)で,| $\quad$ | ハイゼンベルグの不確定性原理(命題4.10)は,科学の命題としては疑わしい文言である |
と考える.ハイゼンベルグは皮肉にも以下のように述べているにもかかわらずである。そう考える理由は,ハイゼンベルグの不確定性原理(命題4.10)は量子力学の命題であるはずにもかかわらず量子力学という言語で書かれていないからで,具体的には,| $(\sharp_1)$ | 命題4.10の中では,「近似測定」と「誤差」に定義が与えられていない |
からある.この問題点は,正式のハイゼンベルグの不確定性原理(後出の定理4.15)で解決された.それでは,\begin{align*}\mbox{なぜ,意味不明なハイゼンベルグの不確定性原理(命題4.10)は有名なのか?}\end{align*}と問うかもしれない.著者は,| $\quad$ | 古典力学との違いを鮮明に打ち出すための「量子力学の宣伝用のキャッチコピー」として,または,「ボーアの相補性の数量的代替」としてハイゼンベルグの不確定性原理(命題4.10)は使われた |
と考える.そして,この「宣伝用のスローガンとしての使い方」は完全に成功した. しかしながら、科学的主張ではないので、当然のこととして、
このようなことは,歴史上はよくあることで,哲学史上最も有名なデカルトのコギト命題(cf. $\S$8.4参照)\begin{align*}「我思う. 故に我在り」\end{align*}も意味不明だとしても, 結果論的には,近代科学の扉を開けたのだと思う.
「ニュートンの林檎」や「アインシュタインのエレベータ」のように、素人が気分を掴めるような物語が、量子力学にも必要で、これがハイゼンベルグの不確定性原理($\gamma$線顕微鏡による思考実験)であると主張したくなる。 |
| $\fbox{注釈4.2}$ | また、「真の値」を「精密測定値」と考えるのは一理あるとして、\begin{align*}\begin{cases}\mbox{位置:}\quad & [x:\mbox{精密測定値(=真の値)}, \quad \widetilde{x}: \mbox{測定値}]\\\mbox{運動量:}\quad & [p:\mbox{精密測定値(=真の値)},\quad \widetilde{p}: \mbox{測定}]\end{cases}\end{align*}と定めよう。| $(\sharp):$ | ここで、誤差を次のように定める。\begin{align*}\Delta_x = | x - \widetilde{x}|,\quad\Delta_p = | p - \widetilde{p}|,\end{align*} |
こう考えると、ハイゼンベルグの不確定性原理((4.20)式)は矛盾を含むとも言える。なぜならば、(4.20)式は精密測定値$(x, p)$が存在しないと主張しているからで、そうなると誤差($\Delta_x$と$\Delta_p$)を定義できなくなってしまう。つまり、「誤差」とは言っても簡単ではない。 |
 ある粒子の位置$x$は精密測定できる.また同様に,運動量$p$も精密測定できる.しかし,位置$x$と運動量$p$を共に精密測定することは不可能で,それぞれの誤差$\Delta x$と$\Delta p$が不可避な近似測定しかできない.
ある粒子の位置$x$は精密測定できる.また同様に,運動量$p$も精密測定できる.しかし,位置$x$と運動量$p$を共に精密測定することは不可能で,それぞれの誤差$\Delta x$と$\Delta p$が不可避な近似測定しかできない.
