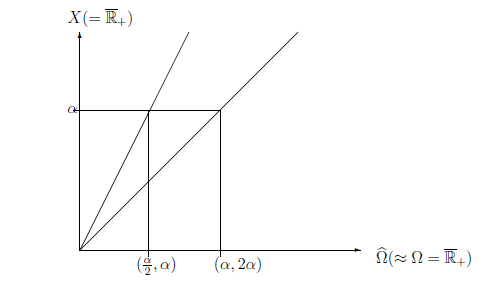5.6: 二つの封筒問題; 非ベイジアン的方法

本節は,次の文献からの抜粋：
$\bullet$ S. Ishikawa; The two envelopes paradox in non-Bayesian and Bayesian statistics arXiv:1408.4916v4 [stat.OT] 2014

ベイズの定理による「二つの封筒問題」へのアプローチは,学部レベルの難しさがあり,それなりにストーリーがあって考えやすい (cf 第9章).しかし,ベイズの定理を使わない方法は,簡単すぎて,とっかかりが無くてむしろ間違いやすい.　高校レベルであるが、以下にこれについて述べる. フィッシャーの最尤法を「二つの封筒問題」に間違って適用する大学院生が稀にいるので、高校レベルと言ってもあなどれない。 モンティホール、三囚人、二つの封筒問題については、Koara 2018　コペンハーゲン解釈；　量子哲学(大学院講義ノート; Webバージョン　453 pp.)(download free)に遊び気分で詳しく書いた。　

5.6.1 二つの封筒問題

次が有名な"二つの封筒問題"である.

問題5.16 [二つの封筒問題] ゲームの主催者は,あなたに二つの封筒 (i.e., 封筒Aと 封筒B)から一つの封筒を選ぶチャンスを提供した. 封筒Aと 封筒Bにそれぞれ $V_1$円と$V_2$円が入っている. あなたには,次が知らされている.

$(a):$ $\qquad \frac{V_1}{V_2}=1/2$ または, $\frac{V_1}{V_2}=2$


交換写像$\overline{x}: \{V_1, V_2 \} \to \{V_1, V_2\} $を \begin{align*} \overline{x} = \begin{cases} V_2,\;\; (\mbox{ if } x=V_1), \\ V_1 \;\; (\mbox{ if } x=V_2) \end{cases} \end{align*} で定める.
$(b):$ あなたは無作為に（公正なコイン投げによって）一方の封筒を 選んだとしよう.
そして, $x_1$円を得たとする. (すなわち, 封筒A[resp B]ならば, $V_1$円[resp. $V_2$円] 得たことになる). このとき, 主催者は,$\overline{x}_1$円得ることになる. したがって,あなたは 「$\overline{x}_1=x_1/2$」 または 「$\overline{x}_1=2x_1$」と推定できる. ここで,あなたには,あなたの$x_1$円と主催者の$\overline{x}_1$円と変更するという選択肢があるとしよう.$x_1=\alpha$としよう. さて,このままにして,$\alpha$円を獲得するか？ または,変更して,$\alpha/2$円または$2\alpha$円を獲得するか？ さて,あなたはどうする.
[(P1):どこがパラドックスなのか　?]. あなたは次のように考えるかもしれない. 確率1/2で, もう一方の封筒$B$は,$\alpha/2$円か,または$2\alpha$円入っているに違いない.　したがって,封筒$B$内のお金の期待値(それをE($\alpha$)と記す)は, \begin{align} E(\alpha)=(1/2)(\alpha/2) + (1/2)(2\alpha)=1.25\alpha \tag{5.22} \end{align} となる.これは封筒$A$の$\alpha$円より大きい. したがって,「封筒$A$を封筒$B$に変更しよう」とあなたは考えるかもしれない.
  • しかし,これはおかしい.　
なぜならば,封筒A と 封筒B の役割は同じはずだからである.あなたがランダムに(i.e., 確率1/2で)選んだのが, 封筒Bだとすると,こんどは封筒Aを選ぶのだろうか？ このパラドクスが,有名な「二つの封筒問題(i.e., "The Other Person's envelope is Always Greener" )」である.

5.6.2 解答: 二つの封筒問題

古典系の基本構造 \begin{align} { [ C_0(\Omega ) \subseteq L^\infty ( \Omega , \nu ) \subseteq B(L^2 ( \Omega , \nu ) ) ] } \end{align} を考えよう。


$X=\overline{\mathbb R}_+ =\{ x \;|\;\mbox{$x$は非負実数} \}$と定める. 二つの連続写像$V_1: \Omega \to \overline{\mathbb R}_+$と$V_2: \Omega \to \overline{\mathbb R}_+$を考える. ここで,たとえば, \begin{align*} V_2(\omega)=2V_1(\omega) \mbox{ または,}\;\; 2V_2(\omega)=V_1(\omega) \quad (\forall \omega \in \Omega ) \end{align*} としてもよいが,そう仮定しなくてもよい. 各$k=1,2$に対して, $L^\infty (\Omega, \nu )$内の 観測量 ${\mathsf O}_k=(X(=\overline{\mathbb R}_+), {\mathcal F}(={\mathcal B}_{\overline{\mathbb R}_+}:\mbox{the Borel field}), F_k )$ を次のように定める \begin{align*} & \qquad [F_k(\Xi )](\omega )= \begin{cases} 1 \qquad & (\mbox{ if } V_k(\omega) \in \Xi) \\ 0 \qquad & (\mbox{ if } V_k(\omega) \notin \Xi) \end{cases} \\ & (\forall \omega \in \Omega, \forall \Xi \in {\mathcal F} ={\mathcal B}_{\overline{\mathbb R}_+} \mbox{ i.e., the Bore field in $X(=\overline{\mathbb R}_+)$ } ) \end{align*} さらに, $L^\infty (\Omega ,\nu)$内の 観測量 ${\mathsf O}=(X, {\mathcal F}, F )$ を以下のように定める. \begin{align} F(\Xi)=\frac{1}{2} \Big( F_1(\Xi)+F_2(\Xi) \Big) \quad (\forall \Xi \in {\mathcal F}) \tag{5.23} \end{align} すなわち, \begin{align*} & \qquad [F(\Xi )](\omega )= \begin{cases} 1 \qquad & (\mbox{ if } V_1(\omega) \in \Xi, \;\; V_2(\omega) \in \Xi) \\ 1/2 \qquad & (\mbox{ if } V_1(\omega) \in \Xi, \;\; V_2(\omega) \notin \Xi) \\ 1/2 \qquad & (\mbox{ if } V_1(\omega) \notin \Xi, \;\; V_2(\omega) \in \Xi) \\ 0\qquad & (\mbox{ if } V_1(\omega) \notin \Xi, \;\; V_2 (\omega) \notin \Xi) \end{cases} \\ & (\forall \omega \in \Omega, \forall \Xi \in {\mathcal F}={\mathcal B}_X \mbox{ i.e., $\Xi$ は $X(=\overline{\mathbb R}_+)$のボレル部分集合 } ) \end{align*} 任意の状態$\omega (\in \Omega )$を未知として,固定する. 測定 ${\mathsf M}_{L^\infty(\Omega, \nu )} ({\mathsf O}=(X, {\mathcal F} , F ), S_{[\omega]})$を考える. 言語ルール1(測定：$\S$2.7) から,次が言える.

$(A_1):$ あなたは,測定 ${\mathsf M}_{L^\infty(\Omega, \nu )} ({\mathsf O}=(X, {\mathcal F} , F ), S_{[\omega_0]})$ によって測定値 $ \left\{\begin{array}{ll} V_1(\omega) \\ V_2(\omega) \end{array}\right\} $ が得られたとする. もちろん,その確率は $ \left\{\begin{array}{ll} 1/2 \\ 1/2 \end{array}\right\} $ である.
ここで金額を変更すれば, $ \left\{\begin{array}{ll} V_2(\omega) \\ V_1(\omega) \end{array}\right\} $円となり, あなたの利得は $ \left\{\begin{array}{ll} V_2(\omega) - V_1(\omega) \\ V_1(\omega) - V_2(\omega) \end{array}\right\} $ 円である.したがって, 変更による利得の期待値は \begin{align*} (V_2(\omega) - V_1(\omega))/2 + ( V_1(\omega) - V_2(\omega))/2 = 0 \end{align*} となる. すなわち, 交換してもしなくても,期待値は同じということになる.よって, "The Other Person's envelope is Always Greener" は当てにならない.


注意5.17問題5.16の条件(a)は不要だった。 この条件は、問題5.16の本質を見誤らせる役割をしている。

5.6.3 別解: 二つの封筒問題5.16

次節($\S$ 5.6.4)の準備のために, 状態空間$\Omega$を$\Omega=\overline{\mathbb R}_+$として, ルベーグ測度$\nu$を仮定する. 古典基本構造 \begin{align*} [ C_0(\Omega ) \subseteq L^\infty ( \Omega , \nu ) \subseteq B(L^2 ( \Omega , \nu ) ) ] \end{align*} を考える.また, $\widehat{\Omega}=\{ (\omega, 2 \omega ) \;| \; \omega \in \overline{\mathbb R}_+ \}$とおいて, \begin{align} \Omega \ni \omega \underset{(同一視)}{\longleftrightarrow} (\omega, 2 \omega ) \in \widehat{\Omega} \tag{5.24} \end{align} を考える. また, $V_1:\Omega (\equiv \overline{\mathbb R}_+) \to X(\equiv \overline{\mathbb R}_+)$と $V_2:\Omega (\equiv \overline{\mathbb R}_+) \to X(\equiv \overline{\mathbb R}_+)$を以下のようにさだめる. \begin{align*} V_1(\omega ) =\omega , \quad V_2(\omega ) = 2 \omega \qquad (\forall \omega \in \Omega) \end{align*} $L^\infty (\Omega, \nu )$内の 観測量 ${\mathsf O}=(X(=\overline{\mathbb R}_+), {\mathcal F}(={\mathcal B}_{\overline{\mathbb R}_+}:\mbox{ the Borel field}), F )$ を以下のように定める. \begin{align*} & \qquad [F(\Xi )](\omega )= \begin{cases} 1 \qquad & (\mbox{ if } \omega \in \Xi, \;\; 2 \omega \in \Xi) \\ 1/2 \qquad & (\mbox{ if } \omega \in \Xi, \;\; 2 \omega \notin \Xi) \\ 1/2 \qquad & (\mbox{ if } \omega \notin \Xi, \;\; 2 \omega \in \Xi) \\ 0 \qquad & (\mbox{ if } \omega \notin \Xi, \;\; 2 \omega \notin \Xi) \end{cases} \qquad (\forall \omega \in \Omega, \forall \Xi \in {\mathcal F} ) \end{align*} 未知の状態$\omega (\in \Omega )$ を固定して, 測定 ${\mathsf M}_{L^\infty (\Omega, \nu )} ({\mathsf O}=(X, {\mathcal F}, F ), S_{[\omega]})$ を考えよう. 言語ルール1(測定:$\S$2.7) によれば,

$(A_2):$ ${\mathsf M}_{L^\infty (\Omega, \nu )} ({\mathsf O}=(X, {\mathcal F}, F ), S_{\omega]})$ によって, 測定値 $x (\in X)$, すなわち, $ \left\{\begin{array}{ll} x=\omega \\ x=2 \omega \end{array}\right\} $ を得る確率は, $ \left\{\begin{array}{ll} 1/2 \\ 1/2 \end{array}\right\} $ である.
ここで,金額を変更すれば, $ \left\{\begin{array}{ll} 2\omega \\ \omega \end{array}\right\} $となり, あなたの変更による利得は $ \left\{\begin{array}{ll} 2\omega - \omega \\ \omega - 2 \omega \end{array}\right\} $ である. よって,変更による利得の期待値は \begin{align*} (2\omega - \omega)/2 + (\omega - 2 \omega)/2 = 0 \end{align*} である. すなわち, 交換してもしなくても,期待値は同じということになる.よって, "The Other Person's envelope is Always Greener" は当てにならない.


注意5.18$\S$5.6.2 と $\S$5.6.3 の解答では、 フィッシャーの最尤法が役立たない。　このことを次節で述べる。

5.6.4: 問題5.16(二つの封筒問題)とフィッシャーの最尤法


さて,測定${\mathsf M}_{L^\infty(\Omega, \nu )} ({\mathsf O}=(X, {\mathcal F}, F ), S_{[\ast]})$によって, 測定値$\alpha$が得られたとしよう. このとき,次の尤度関数を計算しておく.

\begin{align*} f(\alpha, \omega) \equiv \inf_{\omega_1 \in \Omega } \Big[\lim_{\Xi \to \{ x \}, [{F}(\Xi )](\omega_1) \not= 0} \frac{[{F}(\Xi )](\omega)}{ [{F}(\Xi )](\omega_1) } \Big] = \begin{cases} 1 \quad & (\omega = \alpha/2 \mbox{ or }\alpha ) \\ 0 & \mbox{( elsewhere )} \end{cases} \end{align*}

したがって,フィッシャーの最尤法によって,

$(B_1):$ 未知状態$[\ast]$は, $\alpha/2$ または $\alpha$ である.
$\Big($ もし$[\ast]=\alpha/2$ [resp. $[\ast]=\alpha$ ]ならば, 変更による利得は$(\alpha/2-\alpha)$ [resp. $(2\alpha-\alpha)$]となる $\Big)$.
しかしながら, 当然のことであるが,フィッシャーの最尤法は次を主張するわけではない.
$(B_2):$ $ \begin{cases} \mbox{"$[\ast]=\alpha/2$である確率"=1/2　} \\ \mbox{"$[\ast]=\alpha$である確率"=1/2} \\ \mbox{"$[\ast]$がそれ以外の確率"=0} \end{cases} $
は保証されてわけではない. したがって,[(P1): どこがパラドックスなの？]内の文言 「確率1/2で」 が間違っている.

要するに、
$(C):$ 状態空間を明示して,議論すれば,間違いようがない
である。

注意5.19$\quad$(i):問題5.16(二つの封筒問題)において、

  • 仮定(b)は必要不可欠

である。これがないと、観測量 ${\mathsf O}=(X, {\mathcal F}, F )$を(5.23)式で定義することができなくなってしまう。 したがって、仮定(b)がない場合は、「答えがない問題」になってしまう。 ただし、「等確率の原理」, すなわち、
$(\sharp):$ 今選択すべきな状況が$n$個あるとして、どの状況も他の状況と比べて 選択すべき理由が対称的なとき、それぞれの状況を$1/n$の確率で選択とする習慣のことを 「等確率の原理」と言う。

このような、情報が対称的な場合は 公平なコイン投げで決めるという立場を前提にするという立場では、仮定(b)が記載されていなくても、 「等重率に基づいて、観測量${\mathsf O}=(X, {\mathcal F}, F )$が定義できる」という議論が可能である。
本書では、三つの等確率の原理を議論する：

$\qquad$
$(\sharp_1):$ 注意5.19の等確率の原理($\S$5.6)
$(\sharp_2):$ 定理9.18の等確率の原理($\S$9.7)
$(\sharp_3):$ 公準18.4の等確率の原理($\S$18.2)
いずれにしても、

  • 二つの封筒問題は難しい

本書で著者はいくつもの未解決問題を解決しているが ($\S$19.2参照), 二つの封筒問題は最も勘違いしやすい問題の一つと思っている。


(ii): 二つの封筒問題5.16の「ベイズ統計による解答」は, 第9章で述べる.

$\fbox{注釈5.5}$ 読者は次のように考えるかもしれない。
$(\sharp_1):$$\quad$ ([(P1): なぜパラドックス?]で述べたように)問題5.16は 封筒AとBの対称性から直ちに解ける
この解答($\sharp_1$)は間違っているとは言えないかもしれないが、 十分ではない。 なぜならば、
$(\sharp_2):$ "解答($\sharp_1$)は如何なる理論に基づいているのか？" が明らかにされていないからである。
  • 対称性は世界記述法ではない
からである。 (「対称性」と一言で言っても、単純でないことは、$\S$9.3(サンクトペテルスブルグの二つの封筒問題)を見ればわかるだろう). 一方、
  • $\S$5.6.2--$\S$5.6.4の解答は、量子言語に基づいている。
この($\sharp_2$)の観点は重要である。
たとえば、 運動は相対的なのだから、 "地動説(Helicocentrism)　vs. 天動説(Geocentric model)" はどちらとも言えないわけだが、すくなくとも、 次が言える：
$(\sharp_3):$ ニュートン力学を適用する場合は、 天動説よりも地動説の方が考えやすい。
天の邪鬼的な言い方をするならば、
$(\sharp_4):$ アリストテレスの世界観の下では、 地動説よりも天動説の方がしっくりする。
と言える。
したがって、コペルニクス的転回の意味は、 \begin{align} & \fbox{アリストテレスの世界観} \xrightarrow[\mbox{(コペルニクス的転回)}]{} \fbox{ニュートン力学的世界観} \tag{5.25} \end{align} であって、次ではない \begin{align} & \fbox{天動説} \xrightarrow[\mbox{(コペルニクス的転回)}]{} \fbox{地動説} \tag{5.26} \end{align}

式(5.26) は、コペルニクス的転回(5.25)の象徴的な一つの事件に過ぎない。 したがって、 ($\sharp_2$)の問いかけは重要と思う。 本書の唯一の主張は、 図1.1( in $\S$1.1) の「量子言語」なのだから、 量子言語に基づく $\S$5.6.2の解答を主張したい。 問いかけ($\sharp_2$)は、第14章[ゼノンのパラドック]でも重要になる。