6.1 古典量子言語 (= 古典言語ルール1(測定: $\S$2.7) )の復習
あらゆる古典システムはある基本構造
$[ C_0(\Omega ) \subseteq L^\infty (\Omega, \nu ) \subseteq B(L^2 (\Omega, \nu ))]$内で定式化できる.
$[ C_0(\Omega ) \subseteq L^\infty (\Omega, \nu ) \subseteq B(L^2 (\Omega, \nu ))]$
内で定式化された
測定
${\mathsf M}_{L^\infty (\Omega, \nu )} \big({\mathsf O}{{=}} (X, {\cal F} , F{}),
S_{[{}\delta_{\omega_0} ] } \big)$
を
考えよう.
6.1.2 ガウス積分
実直線${\mathbb R}$を考える.
状態空間を
$\Omega = {\mathbb R} \times {\mathbb R}_+$
とする. ここで,
${\mathbb R}_+=\{ \sigma \in {\mathbb R} | \sigma > 0 \}$とする.
さて,
\begin{align*}
\mbox{
古典系の基本構造
$[ C_0(\Omega ) \subseteq L^\infty (\Omega, \nu ) \subseteq B(L^2 (\Omega, \nu ))]$
}
\end{align*}
を考えよう.
$L^\infty (\Omega (\equiv {\mathbb R} \times {\mathbb R}_+))$内の
正規観測量
${\mathsf O}_{G} = ({\mathbb R}, {\mathcal B}_{\mathbb R}, {{{{G}}}} )$
を以下のように定める.
\begin{align}
&
[{{{{G}}}}({\Xi})] ({} {}{\omega} {})
=
\frac{1}{{\sqrt{2 \pi }\sigma{}}}
\int_{{\Xi}} \exp[{}- \frac{({}{}{x} - {}{\mu} {})^2 }{2 \sigma^2} {}] d {}{x}
\tag{6.1}
\\
&
\quad
({}\forall {\Xi} \in {\cal B}_{{\mathbb R}{}}\mbox{(=${\mathbb R}$内のボレル集合体))},
\quad
\forall {}{\omega} =(\mu, \sigma) \in \Omega = {\mathbb R}{}\times {\mathbb R}_+).
\nonumber
\end{align}
$n$を自然数としよう.
$L^\infty ({\mathbb R} \times {\mathbb R}_+)$内の
正規観測量
${\mathsf O}_{G} = ({\mathbb R}, {\mathcal B}_{\mathbb R}, {{{{G}}}} )$
の$n$次同時正規観測量
${\mathsf O}_{G}^n = ({\mathbb R}^n, {\mathcal B}_{\mathbb R}^n, {{{{G}}}^n} )$
を以下のように定める.
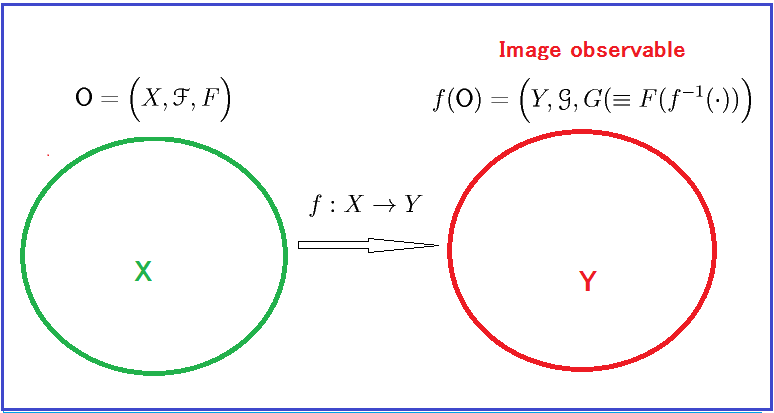
したがって,$L^\infty ({\mathbb R} \times {\mathbb R}_+)$内の二つの
像観測量( Image observable )
$\qquad$要するに、
「測定値たちの平均をとれば、精度が上がる」
ということ。
ここで, $p^{{\chi}^2}_{n-1}({ x} )$
は,
自由度$(n-1)$の
$\chi^2$-分布の確率密度関数,すなわち,
 (A): 古典言語ルール1(古典測定: $\S$2.7) 純粋系
(A): 古典言語ルール1(古典測定: $\S$2.7) 純粋系
言語ルール1(古典系の測定) 純粋型は$\S$2.7で読めるようになったはず
このとき,
測定
${\mathsf M}_{L^\infty (\Omega, \nu )} \bigl({\mathsf O} , S_{[{}\omega_0{}] } \bigl)$
により得られる
測定値$ x$
$(\in X {})$
が,
$ \Xi $
$(\in {\cal F}{})$
に属する確率は,
(もし$F(\Xi)$が$\omega_0$で本質的連続ならば)
$[F(\Xi)](\omega_0)$
で与えられる.

例 6.1 [正規観測量]
例 6.2 [同時正規観測量]
\begin{align}
&
[{{{{G}}}}^n
({\mathop{{{{\times}}}}}_{k=1}^n \Xi_k)]
({}\omega{})
=
{\mathop{{{{\times}}}}}_{k=1}^n
[{{{{G}}}}(\Xi_k)](\omega)
\nonumber
\\
=
&
\frac{1}{({{\sqrt{2 \pi }\sigma{}}})^n}
\underset{
\mathop{{{{\times}}}}_{k=1}^n \Xi_k
}
{\int \cdots \int}
\exp[{}- \frac{\sum_{k=1}^n ({}{}{x_k} - {}{\mu} {})^2
}
{2 \sigma^2} {}] d {}{x_1} d {}{x_2}\cdots dx_n
\tag{6.2}
\\
&
\qquad
({}\forall \Xi_k \in {\cal B}_{{\mathbb R}{}}^{}
({}k=1,2,\ldots, n),
\quad
\forall {}{\omega}=(\mu, \sigma ) \in \Omega = {\mathbb R}\times {\mathbb R}_+{}).
\nonumber
\end{align}
三つの写像
$\overline{\mu}: {\mathbb R}^n \to {\mathbb R}$,
${\overline{SS}}: {\mathbb R}^n \to {\mathbb R}$
そして,
${\overline{\sigma}}: {\mathbb R}^n \to {\mathbb R}$
を次のように定義する.
\begin{align}
&
\overline{\mu}
(x) =
\overline{\mu}
(x_1,x_2,\ldots , x_n ) =
\frac{x_1 + x_2 + \cdots + x_n}{n}
\quad( \forall x=(x_1,x_2,\ldots , x_n ) \in {\mathbb R}^n )
\tag{6.3}
\\
&
{{\overline{SS}}}
(x) =
{{\overline{SS}}}
(x_1,x_2,\ldots , x_n ) =
{\sum_{k=1}^n ( x_k -
\overline{\mu}
(x))^2}
\quad( \forall x=(x_1,x_2,\ldots , x_n ) \in {\mathbb R}^n)
\tag{6.4}
\\
&
{{\overline{\sigma}}}
(x) =
{{\overline{\sigma}}}
(x_1,x_2,\ldots , x_n ) =
\sqrt{
\frac
{\sum_{k=1}^n ( x_k -
\overline{\mu}
(x))^2}
{n}
}
\quad( \forall x=(x_1,x_2,\ldots , x_n ) \in {\mathbb R}^n)
\tag{6.5}
\end{align}
が次のように定まる.
以下の計算(「ガウス積分」という計算(6.6)と(6.7))は簡単というわけではないが,大学2年次の数学内の問題である.
\begin{align}
&
[({{{{G}}}^n} \circ \overline{\mu}^{-1})(\Xi_1)](\omega)
\nonumber
\\
=
&
\frac{1}{({{\sqrt{2 \pi }\sigma{}}})^n}
\underset{
\{ x \in {\mathbb R}^n \;:\; {\overline{\mu}}(x) \in \Xi_1 \}}
{\int \cdots \int}
\exp[{}- \frac{\sum_{k=1}^n ({}{}{x_k} - {}{\mu} {})^2
}
{2 \sigma^2} {}] d {}{x_1} d {}{x_2}\cdots dx_n
\nonumber
\\
=
&
\frac{\sqrt{n}}{{\sqrt{2 \pi }\sigma{}}}
\int_{{\Xi_1}} \exp[{}- \frac{n({}{}{x} - {}{\mu} {})^2 }{2 \sigma^2} {}] d {}{x}
\tag{6.6}
\\
=
&
\frac{1}{2 \pi\frac{\sigma}{\sqrt{n}} }
\int_{{\Xi_1}} \exp[{}- \frac{({}{}{x} - {}{\mu} {})^2 }{2 (\frac{\sigma}{\sqrt{n}})^2} {}] d {}{x}
\\
&
\quad
({}\forall {\Xi_1} \in {\cal B}_{{\mathbb R}{}},
\;\;
\quad
\forall {}{\omega} =(\mu, \sigma) \in \Omega \equiv {\mathbb R}{}\times {\mathbb R}_+).
\end{align}
\begin{align}
&
[({{{{G}}}^n} \circ {{{\overline{SS}}}}^{-1})(\Xi_2)](\omega)
\nonumber
\\
=
&
\frac{1}{({{\sqrt{2 \pi }\sigma{}}})^n}
\underset{
\{ x \in {\mathbb R}^n \;:\; {\overline{SS}}(x) \in \Xi_2 \}}
{\int \cdots \int}
\exp[{}- \frac{\sum_{k=1}^n ({}{}{x_k} - {}{\mu} {})^2
}
{2 \sigma^2} {}] d {}{x_1} d {}{x_2}\cdots dx_n
\nonumber
\\
=
&
\int_{\Xi_2 / \sigma^2} p^{{\chi}^2}_{n-1}({ x} ) {dx}
\tag{6.7}
\\
&
\quad
(
\;\;
\forall \Xi_2 \in {\cal B}_{{\mathbb R}_+{}},
\quad
\forall {}{\omega} =(\mu, \sigma) \in \Omega \equiv {\mathbb R}{}\times {\mathbb R}_+).
\nonumber
\end{align}
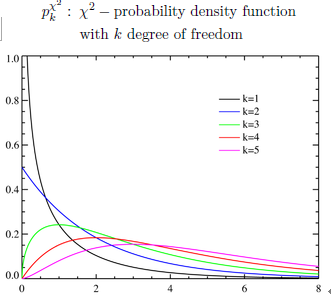
6.1: 量子言語 (= 言語ルール1(測定: $\S$2.7) )の復習:カイ二乗分布
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
