6.2:信頼区間法と統計的仮説検定の逆関係

目次:
信頼区間法と統計的仮説検定の逆の関係(コインの裏表の関係)について述べる. ここでは,古典系の基本構造 \begin{align} [ C_0(\Omega ) \subseteq L^\infty (\Omega, \nu ) \subseteq B(L^2 (\Omega, \nu ))] \end{align} に集中する。

6.2.1: 信頼区間法

可換$W^*$-代数 ${L^\infty (\Omega)}$内の 観測量 ${\mathsf O} = ({}X, {\cal F} , F{}){}$ を考える. 局所コンパクト空間$\Theta$ (第2状態空間)は次の 半距離$d^x_{\Theta}$ $(\forall x \in X)$を持つ. すなわち, 各$x\in X$に対して, 半距離 と呼ばれる写像： $d^x_{\Theta}: \Theta^2 \to [0,\infty)$ は次を満たす：

$(i):$ $\qquad$ $d^x_\Theta (\theta, \theta )=0$,
$(ii):$ $\qquad$ $d^x_\Theta (\theta_1, \theta_2 )$ $=d^x_\Theta (\theta_2, \theta_1 )$,
$(iii):$ $\qquad$ $d^x_\Theta (\theta_1, \theta_3 )$ $\le d^x_\Theta (\theta_1, \theta_2 ) + d^x_\Theta (\theta_2, \theta_3 ) $.


二つの写像 $E:X \to \Theta$ と $\pi: \Omega \to \Theta$ を考える. 写像 $E:X \to \Theta$ は 推定量, 写像 $\pi: \Omega \to \Theta$ は システム量 と呼ばれる.

定理 6.3 [信頼区間法].
正数 $\alpha$ を $0 < \alpha \ll 1$, としよう. たとえば, $\alpha = 0.05$ とする. 任意の状態 $ \omega ({}\in \Omega)$ に対して, 正数 $\eta^{1-\alpha}_{\omega}$ $({}> 0)$ を次のように定義する.($1-\alpha=\gamma$として,$\eta^{\gamma}_{\omega}$と書くことも多々ある). \begin{align} \eta^{1-\alpha}_{\omega} = \inf \{ \eta > 0: [F(\{ x \in X \;:\; d^x_\Theta ( E(x) , \pi( \omega ) ) < \eta \} )](\omega ) \ge {1-\alpha} \} \tag{6.9} \end{align} 次は自明である.
$(A):$ 測定 ${\mathsf M}_{L^\infty (\Omega)} \big({}{\mathsf O}:= ({}X, {\cal F} , F{}) ,$ $ S_{[\omega_0 {}] } \big)$ によって得られた測定値$x$が次を満たす確率は, ${1-\alpha}$(e.g., ${1-\alpha}= 0.95)$以上である：
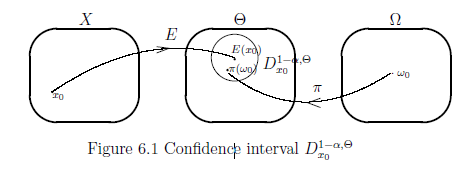
\begin{align} d^x_\Theta (E(x), \pi(\omega_0){}) < {\eta }^{1-\alpha}_{\omega_0} \tag{6.10} \end{align}

更に,$({}{1-\alpha}{})$-信頼区間と呼ばれる 領域$D_x^{1-\alpha}$ $(\subseteq \Theta)$ ) を以下のように定義する. \begin{align} D_x^{1-\alpha} = \{ \pi(\omega) (\in \Theta) : d^x_\Theta ({}E(x), \pi(\omega ) ) < \eta^{1-\alpha}_{\omega } \}. \tag{6.11} \end{align} ここで, 次の同値性は明らか. \begin{align} (6.10) \; \Longleftrightarrow \; \; D_{x}^{1-\alpha} \ni \pi (\omega_0). \tag{6.12} \end{align}

注意6.4 [(B$_1$):信頼区間の意味]. 並行測定 $\bigotimes_{j=1}^J {\mathsf M}_{L^\infty (\Omega)} \big({\mathsf O}:= (X, {\cal F} , F) ,$ $ S_{[\omega_0 ] } \big)$を考えて、 その測定値を$x=(x_1,x_2, \ldots , x_J)( \in X^J)$としよう。 このとき,定理6.3の主張は,次と同じである. \begin{align} \lim_{J \to \infty } \frac{\mbox{Num} [\{ j \;|\; D_{x_j}^{{1-\alpha}} \ni \pi( \omega_0)]}{J} \ge {1-\alpha} (= 0.95) \tag{6.13} \end{align} ここに, $\mbox{Num} [A]$は集合$A$の要素の個数とする.


[(B$_2$)] $\eta_\omega^{1-\alpha}=\eta_\omega^\alpha$]. 次に注意しよう. \begin{align} (6.9)& = \eta_\omega^{1-\alpha} = \inf \{ \eta > 0: [F(\{ x \in X \;:\; d^x_\Theta ( E(x) , \pi( \omega ) ) < \eta \} )](\omega ) \ge {1-\alpha} \} \nonumber \\ &= \inf \{ \eta > 0: [F(\{ x \in X \;:\; d^x_\Theta ( E(x) , \pi( \omega ) ) \ge \eta \} )](\omega ) \le \alpha \} \tag{6.14} \end{align} である.

6.2.2 仮説検定

統計的仮説検定の説明をしよう. 信頼区間法とは,「コインの裏表」の関係にあることを注意して次を読んで欲しい.

定理 6.5 [統計的仮説検定]
正数$\alpha$ を $0 < \alpha \ll 1$としよう. たとえば, $\alpha = 0.05$ としよう. 任意の状態 $ \omega ({}\in \Omega)$に対して, 正数 $\eta^\alpha_{\omega}$ $({}> 0)$ を次のように定義する. \begin{align} \small{ \eta^\alpha_{\omega} = \inf \{ \eta > 0: [F(\{ x \in X \;:\; d^x_\Theta ( E(x) , \pi( \omega ) ) \ge \eta \} )](\omega ) \le \alpha \} \Big( = (6.14)=\eta_\omega^{1- \alpha} \Big) } \tag{6.15} \end{align} このとき,次は自明である.
$(C):$ 測定 ${\mathsf M}_{L^\infty (\Omega)} \big({}{\mathsf O}:= ({}X, {\cal F} , F{}) ,$ $ S_{[\omega_0 {}] } \big)$ によって得られた測定値$x$が次を満たす確率は, $\alpha$(e.g., $\alpha= 0.05)$以下である：
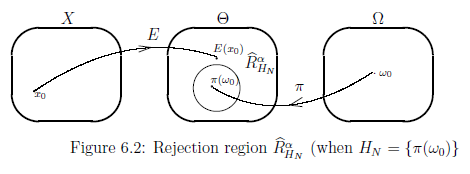
\begin{align} d^x_\Theta (E(x), \pi(\omega_0){}) \ge {\eta }^\alpha_{\omega_0} . \tag{6.16} \end{align}

ここで,帰無仮説 ${H_N}$ $( \subseteq \Theta )$ の$({}\alpha{})$-棄却域を 以下のように定める. \begin{align} & {\widehat R}_{H_N}^{\alpha} = \bigcap_{\omega \in \Omega \mbox{ such that } \pi(\omega) \in {H_N}} \{ E({x}) (\in \Theta) : d^x_\Theta ({}E(x), \pi(\omega ) ) \ge \eta^\alpha_{\omega } \} \tag{6.17} \end{align} 明らかに,次が言える.
$(D):$ $\pi(\omega_0) \in H_N$としよう. 測定 ${\mathsf M}_{L^\infty (\Omega)} \big({}{\mathsf O}:= ({}X, {\cal F} , F{}) ,$ $ S_{[\omega_0 {}] } \big)$ によって得られた測定値$x$が次を満たす確率は, $\alpha$(e.g., $\alpha= 0.05)$以下である：
\begin{align} {\widehat R}_{H_N}^\alpha \ni E(x). \tag{6.18} \end{align}

6.2,3: 信頼区間法と仮説検定の逆関係
系6.6[信頼区間法と仮説検定の逆関係]

$0 < \alpha \ll 1$とする. 可換$W^*$-代数 ${L^\infty (\Omega)}$内の 観測量 ${\mathsf O} = ({}X, {\cal F} , F{}){}$ を考える. $\Theta$を局所コンパクト空間として, 二つの写像 $E:X \to \Theta$ と $\pi: \Omega \to \Theta$ を考える. 写像 $E:X \to \Theta$ は推定量, 写像 $\pi: \Omega \to \Theta$ はシステム量と呼ばれる. $\eta_\omega^{1-\alpha}$は(6.9)で, $\eta_\omega^\alpha$は(6.15)で定める.

$(E):$ [信頼区間法]. 任意の$x \in X$に対して,$({}1- \alpha{})$-信頼区間を以下のように定める. \begin{align} & D_{x}^{1- \alpha, \Theta } = \{ \pi(\omega) (\in \Theta) : d^x_\Theta ({}E(x), \pi(\omega ) ) < \eta^{1- \alpha}_{\omega } \} \tag{6.19} \end{align} または, \begin{align} & D_{x}^{1- \alpha, \Omega} = \{ \omega (\in \Omega) : d^x_\Theta ({}E(x), \pi(\omega ) ) < \eta^{1- \alpha}_{\omega } \} \tag{6.20} \end{align} さて, 測定 ${\mathsf M}_{L^\infty (\Omega)} \big({}{\mathsf O}:= ({}X, {\cal F} , F{}) ,$ $ S_{[\omega_0 {}] } \big)$ によって,測定値$x (\in X)$が得られたとしよう. このとき, \begin{align*} D_x^{1-\alpha, \Theta} \ni \pi(\omega_0) \quad \mbox{ また,同じ意味で } \quad D_x^{1-\alpha, \Omega} \ni \omega_0 \end{align*} である確率は,$1- \alpha$以上である.
$(F):$ [統計的仮説検定]. $H_N ( \subseteq \Theta )$を 帰無仮説として,状態$\omega_0$は次をみたすと仮定しよう. \begin{align*}\pi(\omega_0) \in H_N ( \subseteq \Theta ) \end{align*} ここで, \begin{align} & {\widehat R}_{{H_N}}^{\alpha; \Theta} = \bigcap_{\omega \in \Omega \mbox{ such that } \pi(\omega) \in {H_N}} \{ E({x}) (\in \Theta) : d^x_\Theta ({}E(x), \pi(\omega ) ) \ge \eta^\alpha_{\omega } \}. \tag{6.21} \end{align} または, \begin{align} & \small{ {\widehat R}_{{H_N}}^{\alpha; X} = E^{-1}( {\widehat R}_{{H_N}}^{\alpha; \Theta}) = \bigcap_{\omega \in \Omega \mbox{ such that } \pi(\omega) \in {H_N}} \{ x (\in X) : d^x_\Theta ({}E(x), \pi(\omega ) ) \ge \eta^\alpha_{\omega } \}. } \tag{6.22} \end{align} として,これらを,帰無仮説 ${H_N}$の$({}\alpha{})$-棄却域と呼ぶ.

さて, 測定 ${\mathsf M}_{L^\infty (\Omega)} \big({}{\mathsf O}:= ({}X, {\cal F} , F{}) ,$ $ S_{[\omega_0 {}] } \big)$ によって,測定値$x (\in X)$が得られたとしよう. このとき, \begin{align} "E(x) \in {\widehat R}_{{H_N}}^{\alpha; \Theta}" \quad \mbox{ また,同じ意味で } \quad "x \in {\widehat R}_{{H_N}}^{\alpha; X}" \tag{6.23} \end{align} である確率は,$\alpha$以下である.