6.3.3: 仮説検定[帰無仮説$H_N=\{\mu_0\}( \subseteq \Theta = {\mathbb R}$)]
問題:
$x_1, x_2, .... x_n $を正規分布$N(\mu, \sigma )$
(母平均$\mu$は未知、母分散$\sigma$は既知)から得られたデータとする。
このとき、我々の問題は
問題6.9 [仮説検定]
同時正規測定
${\mathsf M}_{L^\infty ({\mathbb R} \times {\mathbb R}_+)}$
$({\mathsf O}_G^n = ({\mathbb R}^n, {\mathcal B}_{\mathbb R}^n, {{{G}}^n}) ,$
$S_{[(\mu, \sigma)]})$
を考えよう.ここで,
\begin{align*}
\mu = \mu_0
\end{align*}
と仮定しよう.すなわち,帰無仮説を$H_N=\{ \mu_0 \}$
$(\subseteq
\Theta=
{\mathbb R} )
)$
と仮定する.$0 < \alpha \ll 1$とする.
このとき,次を満たす${\widehat R}_{{H_N}}^{\alpha; \Theta}( \subseteq \Theta)$で,「出来るだけ大きいもの($\sigma$に依存してもよい)」を見つけよ
とする.
任意の状態
$ \omega=(\mu, \sigma ) ({}\in \Omega=
{\mathbb R} \times {\mathbb R}_+ )$
に対して,
正数
$\eta^\alpha_{\omega}$
$({}> 0)$
を以下のように定める.
ここに,
${{\rm Ball}^c_{d_{\Theta}^{(1)}}}(\pi( \omega ) ; \eta)$
$=$
$\{ \theta
({}\in\Theta):
d_{\Theta}^{(1)} ({}\mu, \theta {}) \ge \eta \}$
$=
\Big(
( -\infty, \mu - \eta] \cup [\mu + \eta , \infty )
\Big)
$である.
6.3(2): 母平均 (仮説検定 )
ネイマン=ピアソン流の仮説検定の伝統からと思うが、
という言葉がよく使われている。 これらの言葉も慣れれば、違和感なしに使えるようになるのかもしれないが、
統計学の専門外である著者にはなかなか馴染めない。「両側検定、片側検定」もわかりにくい。
統計学の本では、「分かり易い説明」のつもりかもしれないが、かえって分かりにくくすると考える。
したがって、本書では、これらの言葉は使わない。
目次
である。
この問題を量子言語で書き換えると、以下のようになる。
$\bullet$
${\mathsf M}_{L^\infty ({\mathbb R} \times {\mathbb R}_+)}$
$({\mathsf O}_G^n = ({\mathbb R}^n, {\mathcal B}_{\mathbb R}^n, {{{G}}^n}) ,$
$S_{[(\mu_0, \sigma)]})$の測定値$x(\in{\mathbb R}^n )$が,
\begin{align*}
E(x) \in {\widehat R}_{{H_N}}^{\alpha; \Theta}
\end{align*}
を満たす確率は,$\alpha$以下である.
- (ガウス積分の公式(6.6)の導出は意外と難しい)
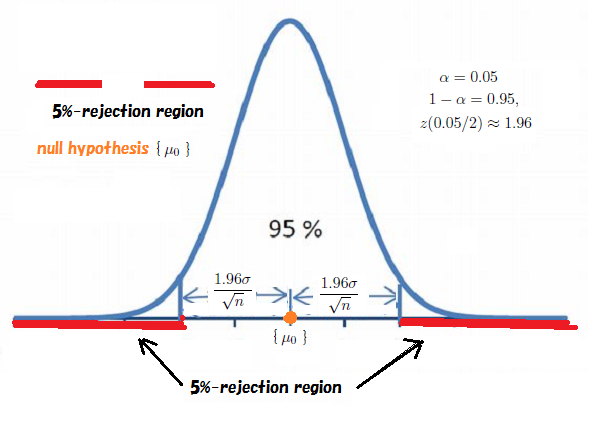
したがって, ${\widehat R}_{H_N}^{\alpha}$ ( $(\alpha)$-棄却域 of $H_N (= \{ \mu_0\} \subseteq \Theta (= {\mathbb R}))$ ) を次のように得る。
\begin{align} {\widehat R}_{\{ \mu_0 \}}^{\alpha, \Theta} & = \bigcap_{\pi(\omega ) =\mu \in \{ \mu_0 \} } \{ {E(x)} (\in \Theta= {\mathbb R}) : d_{\Theta}^{(1)} (E(x), \pi (\omega)) \ge \eta^\alpha_{\omega } \} \nonumber \\ & = \{ E(x) (= \frac{x_1+ \ldots + x_n}{n}) \in {\mathbb R} \;:\; |\overline{\mu}(x) - \mu_0 | = | \frac{x_1+ \ldots + x_n}{n} - \mu_0 | \ge \frac{\sigma}{\sqrt{n}} z(\frac{\alpha}{2}) \} \\ & \tag{6.35} \end{align}帰無仮説$H_N (= \{ \mu_0\} \subseteq \Theta (= {\mathbb R}))$ の ${}(\alpha{})$-棄却域${\widehat R}_{H_N}^{\alpha, \Theta}$ は$\sigma$に依存する. したがって, \begin{align} & \small{ {\widehat R}_{\{ \mu_0 \} \times {\mathbb R}_+}^{\alpha, \Theta} = \{ (\overline{\mu}(x), \sigma) \in {\mathbb R} \times {\mathbb R}_+ \;:\; | \mu_0 - \overline{\mu}(x)| = | \mu_0 - \frac{x_1+ \ldots + x_n}{n}| \ge \frac{\sigma}{\sqrt{n}} z(\frac{\alpha}{2}) \} } \\ & \tag{6.36} \end{align} として, 図示する.
6.3.4: 仮説検定 [帰無仮説$H_N=( -\infty , \mu_0] (\subseteq \Theta (={\mathbb R})$)]
問題: $x_1, x_2, .... x_n $を正規分布$N(\mu, \sigma )$ (母平均$\mu$は未知、母分散$\sigma$は既知)から得られたデータとする。 このとき、我々の問題は
- $\mu \le \mu_0$と仮定したとき、「$ \frac{x_1 + x_2 + ...+ x_n }{n} -\mu_0 > \delta |$」は滅多に起きないような、最小の$\delta$をもとめよ
である。
この問題を量子言語で書き換えると、以下のようになる。
| $\bullet$ | ${\mathsf M}_{L^\infty ({\mathbb R} \times {\mathbb R}_+)}$ $({\mathsf O}_G^n = ({\mathbb R}^n, {\mathcal B}_{\mathbb R}^n, {{{G}}^n}) ,$ $S_{[(\mu_0, \sigma)]})$の測定値$x(\in{\mathbb R}^n )$が, \begin{align*} E(x) \in {\widehat R}_{{H_N}}^{\alpha; \Theta} \end{align*} を満たす確率は,$\alpha$以下である. |
[帰無仮説$H_N=( -\infty , \mu_0] \subseteq \Theta (={\mathbb R})$の棄却域].
$L^\infty ({\mathbb R} \times {\mathbb R}_+)$内の
同時測定
${\mathsf M}_{L^\infty ({\mathbb R} \times {\mathbb R}_+)}$
$({\mathsf O}_N^n = ({\mathbb R}^n, {\mathcal B}_{\mathbb R}^n, {{{G}}^n}) ,$
$S_{[(\mu, \sigma)]})$
を考える。
ここで、
$\Omega = {\mathbb R} \times {\mathbb R}$,
$X={\mathbb R}^n$
とする。
状態$\omega = (\mu, \sigma ) \in \Omega $
において、$\sigma$を固定しておく。
したがって、
\begin{align*}
\Theta = {\mathbb R}
\end{align*}
と置く。
式 (6.3)によって、
推定量
$E: {\mathbb R}^n \to \Theta (\equiv {\mathbb R} )$
を次のように考える:
\begin{align}
E(x)=
=
\overline{\mu}(x)
=
\frac{x_1 + x_2 + \cdots + x_n}{n}
\tag{6.37}
\end{align}
また、システム量$\pi: \Omega \to \Theta $
を次のように考える:
\begin{align*}
\Omega={\mathbb R} \times {\mathbb R}_+
\ni
\omega = (\mu, \sigma )
\mapsto \pi (\omega ) = \mu \in \Theta={\mathbb R}
\end{align*}
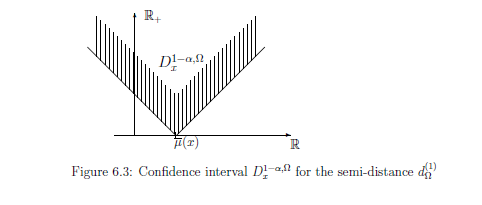
さらに、$\Theta (={\mathbb R} )$内の半距離 $d_{\Theta}^{(2)}$
を次のように定める.
\begin{align}
d_{\Theta}^{(2)}((\theta_1, \theta_2)
=
\begin{cases}
|\theta_1 - \theta_2| \quad & \mu_0 \le \theta_1, \theta_2
\\
|\theta_2 - \mu_0| \quad & \theta_1 \le \mu_0 \le \theta_2
\\
|\theta_1 - \mu_0| \quad & \theta_2 \le \mu_0 \le \theta_1
\\
0 \quad & \theta_1 , \theta_2 \le \mu_0
\end{cases}
\tag{6.38}
\end{align}
任意の
$ \omega=(\mu, \sigma ) ({}\in \Omega=
{\mathbb R} \times {\mathbb R}_+ )$に対して,
正数
$\eta^\alpha_{\omega}$
$({}> 0)$
を次のように定める.
\begin{align}
\eta^\alpha_{\omega}
=
\sup
\{
\eta > 0:
[G^n ({}E^{-1} ({}
{ {\rm Ball}^c_{d_{\Theta}^{(2)}}}(\pi(\omega) ; \eta{}))](\omega )
\le \alpha
\}
\nonumber
\end{align}
ここで,
$\pi(\omega )=\mu \in H_N=( - \infty , \mu_0]$としよう.
このとき,
\begin{align}
&
E^{-1}({{\rm Ball}^c_{d_{\Theta}^{(2)}}}(\pi (\omega) ; \eta ))
\nonumber
\\
\subseteq
&
E^{-1}
\Big(
[\mu + \eta , \infty )
\Big)
\nonumber
\\
=
&
\{
(x_1, \ldots , x_n )
\in {\mathbb R}^n
\;:
\;
\mu + \eta
\le
\frac{x_1+\ldots + x_n }{n}
\}
\nonumber
\\
=
&
\{
(x_1, \ldots , x_n )
\in {\mathbb R}^n
\;:
\;
\frac{(x_1- \mu)+\ldots + (x_n- \mu) }{n}
\ge \eta
\}
\tag{6.39}
\end{align}
よって,
\begin{align}
&
[{{{G}}}^n
(E^{-1}({{\rm Ball}^c_{d_{\Theta}^{(2)}}}(\pi(\omega) ; \eta ))]
({}\omega{})
\nonumber
\\
\le
&
\frac{1}{({{\sqrt{2 \pi }\sigma{}}})^n}
\underset{{
\frac{(x_1- \mu)+\ldots + (x_n- \mu) }{n}
\ge \eta
}}{\int \cdots \int}
\exp[{}- \frac{\sum_{k=1}^n ({}{}{x_k} - {}{\mu} {})^2
}
{2 \sigma^2} {}] d {}{x_1} d {}{x_2}\cdots dx_n
\nonumber
\\
=
&
\frac{1}{({{\sqrt{2 \pi }\sigma{}}})^n}
\underset{{
\frac{x_1+\ldots + x_n }{n}
\ge \eta
}}{\int \cdots \int}
\exp[{}- \frac{\sum_{k=1}^n ({}{}{x_k} {}{} {})^2
}
{2 \sigma^2} {}] d {}{x_1} d {}{x_2}\cdots dx_n
\nonumber
\end{align}
ここで,ガウス積分(6.6)より,
\begin{align}
=
&
\frac{\sqrt{n}}{{\sqrt{2 \pi }\sigma{}}}
\int_{{x \ge \eta}} \exp[{}- \frac{{n}{x}^2 }{2 \sigma^2}] d {x}
=
\frac{1}{{\sqrt{2 \pi }{}}}
\int_{{x \ge \sqrt{n} \eta/\sigma}} \exp[{}- \frac{{x}^2 }{2 }] d {x}
\tag{6.40}
\end{align}
したがって,次の方程式を解いて,
\begin{align}
\frac{1}{{\sqrt{2 \pi }{}}}
\int_{z(\alpha)}^{\infty} \exp[{}- \frac{{x}^2 }{2 }] d {x}
=
{\alpha}
\tag{6.41}
\end{align}
次を得る.
\begin{align}
\eta^\alpha_{\omega} =
\frac{\sigma}{\sqrt{n}}
z({\alpha})
\tag{6.42}
\end{align}
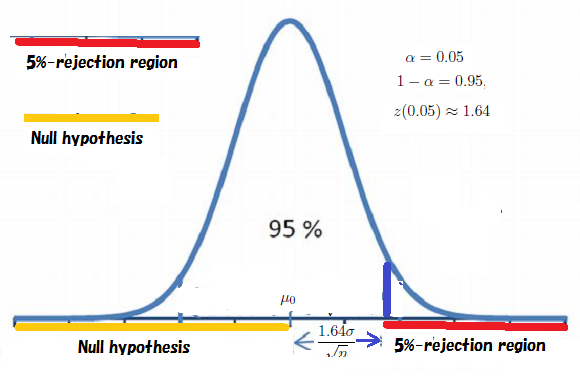
したがって,
帰無仮説$H_N
= (-\infty, \mu_0]( \subseteq \Theta = {\mathbb R})$
の
${}(\alpha{})$-棄却域${\widehat R}_{H_N}^{\alpha, \Theta}$
を次のように得る.
\begin{align}
{\widehat R}_{ ( - \infty , \mu_0]}^{\alpha, \Theta}
&
=
\bigcap_{\pi(\omega ) = \mu \in ( - \infty , \mu_0] }
\{
{E(x)}
(\in
\Theta=
{\mathbb R})
:
d_{\Theta}^{(2)} ({}E(x),
\pi (\omega))
\ge
\eta^\alpha_{\omega }
\}
\nonumber
\\
&
=
\{ E(x) (= \frac{x_1+ \ldots + x_n}{n}) \in {\mathbb R}
\;:\;
\frac{x_1+ \ldots + x_n}{n} - \mu_0
\ge
\frac{\sigma}{\sqrt{n}}
z({\alpha})
\}
\tag{6.43}
\end{align}
さらに,注意6.10と同様に, $\sigma$に依存することを強調するならば, \begin{align} & \small{ {\widehat R}_{( - \infty, \mu_0 ] \times {\mathbb R}_+}^{\alpha,\Theta} = \{ (E(x) (= \frac{x_1+ \ldots + x_n}{n}), \sigma) \in {\mathbb R} \times {\mathbb R}_+ \;:\; \frac{x_1+ \ldots + x_n}{n} - \mu_0 \ge \frac{\sigma}{\sqrt{n}} z({\alpha}) \} } \\ & \tag{6.44} \end{align} として,以下のように図示できる.