定義8.1[(=定義3.19):擬積観測量観測量 ]

基本構造$[ {\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]$ を考える. $\overline{\mathcal A}$内の観測量 ${\mathsf O}_{12...n}$ ${{=}}$ $({{{\times}}}_{k=1}^n X_k ,$ $ \boxtimes_{k=1}^n{\cal F}_k , $ ${F}_{12...n}{})$ は次を満たすとする: \begin{align} & {F}_{12...n}(X_1 \times \cdots \times X_{k-1} \times \Xi_k \times X_{k+1} \times \cdots \times X_n ) = F_k (\Xi_k) \tag{8.1} \\ & \quad \qquad \qquad (\forall \Xi_k \in {\cal F}_k , \forall k =1,2,\ldots,n ) \nonumber \end{align} このとき， 観測量 ${\mathsf O}_{12...n}$ ${{=}}$ $({{{\times}}}_{k=1}^n X_k ,$ $ \boxtimes_{k=1}^n{\cal F}_k , $ ${F}_{12...n}{})$ は $\{ {\mathsf O}_k \; | \;k=1,2,\ldots,n \}$ の 擬積観測量 と呼ばれ， 次のように記される： \begin{align*} {\mathop{\times}^{pq}_{k=1,2,\ldots,n}}{\mathsf O}_k = ({{{\times}}}_{k=1}^n X_k , \boxtimes_{k=1}^n{\cal F}_k, {\mathop{\times}^{pq}_{k=1,2,\ldots,n} }F_k{}) \end{align*}

もちろん， 同時観測量も 擬積観測量の一種で， したがって， 擬積観測量は，一般には存在するとは限らないし, また存在したとしても一般には 一意に決まらない． もちろん,古典系の基本構造 $[C_0(\Omega) \subseteq L^\infty(\Omega \subseteq B(L^2(\Omega )]$ の場合は,必ず同時観測量が存在する.

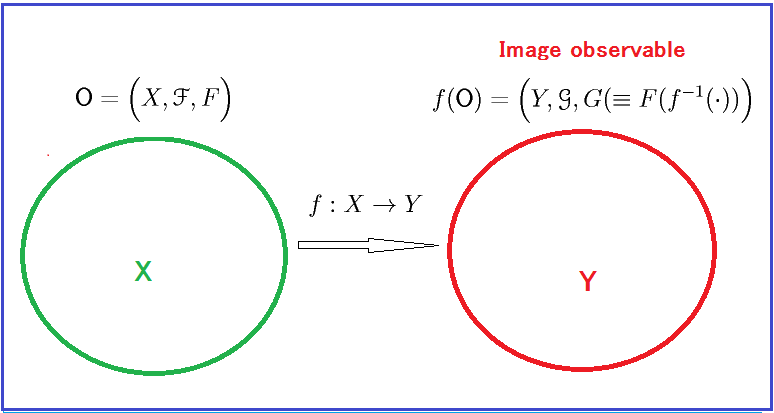
定義8.2[像観測量, 辺観測量] 基本構造$[ {\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]$と$\overline{\mathcal A}$内の観測量 ${\mathsf O}$ ${{=}}$ $( X,$ ${\cal F} , $ ${F})$を考えよう。 可測空間$(Y, {\mathcal G})$ bemeasurable 空間と可測写像$f: X \to Y $を考える。$\overline{\mathcal A}$内の像観測量 $f( {\mathsf O})$ ${{=}}$ $( Y,$ ${\cal G} , $ ${F}\circ f^{-1})$ を次のように定める：

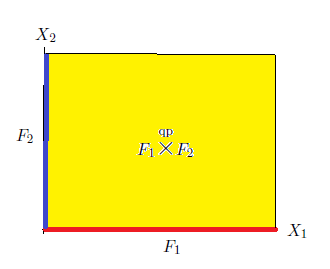
\begin{align} ( {F}\circ f^{-1} ) (\Gamma ) = F( f^{-1}(\Gamma )) \qquad (\forall \Gamma \in {\mathcal G} ) \end{align}

[辺観測量 ]$\overline{\mathcal A}$内の観測量 ${\mathsf O}_{12...n}$ ${{=}}$ $(\times_{k=1}^n X_k ,$ $ \boxtimes_{k=1}^n{\cal F}_k , $ ${F}_{12...n})$ in $\overline{\mathcal A}$を考える。 $1{{\; \leqq \;}}j {{\; \leqq \;}}n$である自然数$j$に対して, ${F}^{(j)}_{12...n}$を次のように定めて、

\begin{align} {F}^{(j)}_{12...n} (\Xi_j) = F_{12...n}(X_1 \times \cdots \times X_{j-1} \times \Xi_j \times X_{j+1} \times \cdots \times X_{n}) \quad ( \forall \Xi_j \in {\cal F}_j ) \end{align}

観測量 ${\mathsf O}^{(j)}_{12...n}$ ${{=}}$ $(X_j ,$ $ {\cal F}_j , $ ${F}^{(j)}_{12...n})$を得る。 この ${\mathsf O}^{(j)}_{12...n}$ を ${\mathsf O}_{12...n}$ の 辺観測量 (正確には， $(j)$-辺観測量 ) と呼ぶ．これは、写像$f_j: X_1 \times X_2 \times ... \times X_n \to X_j$: $$ f_j ( x_1, x_2 , ..., x_j,..., x_n ) = x_j $$ に関する観測量 ${\mathsf O}_{12...n}$の像観測量である。
これは，一般化できる． たとえば， ${\mathsf O}_{12...n}^{(12)}$ ${{=}}$ $( X_1 \times X_2 ,$ $ {\cal F}_1 \boxtimes {\cal F}_2, $ ${F}^{(12)}_{12...n}{})$を， \begin{align*} {F}^{(12)}_{12...n}(\Xi_1 \times \Xi_2) = F^{(12)}_{12...n}(\Xi_1 \times \Xi_2 \times X_3 \times \cdots \times X_{n}) \quad ( \forall \Xi_1 \in {\cal F}_1, \forall \Xi_2 \in {\cal F}_2 ) \end{align*} と定めれば， ${\mathsf O}_{12...n}^{(12)}$ ${{=}}$ $( X_1 \times X_2 ,$ $ {\cal F}_1 \boxtimes {\cal F}_2, $ ${F}^{(12)}_{12...n}{})$ は辺観測量(「面観測量」というべきかもしれないが) となる． したがって，もちろん， ${F}_{12...n}={F}^{(12...n)}_{12...n}{}$ である．


以下の定理は,しばしば使われる.
定理 8.3$\quad$ 基本構造$[ {\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]$ を考える. $\overline{\mathcal A}$内の観測量 ${\mathsf O}_1$ ${{=}}$ $(X_1 , $ ${\cal F}_1 , $ $F_1{})$ と 射影観測量${\mathsf O}_1$ ${{=}}$ $(X_2 , $ ${\cal F}_2 , $ $F_2{})$ を考える．このとき,次の(A$_1$)と(A$_2$)は同値である.
$(A_1):$ ${\mathsf O}_1$と${\mathsf O}_2$は可換,すなわち, \begin{align*} F_1(\Xi_1 ) F_2(\Xi_2 ) = F_2(\Xi_2 ) F_1(\Xi_1 ) \qquad (\forall \Xi_1 \in {\mathcal F}_1, \forall \Xi_2 \in {\mathcal F}_2 ) \end{align*}
$(A_2):$ 次を満たす$\overline{\mathcal A}$内の観測量${\mathsf O}_{12}$ $ {{=}} (X_1\times X_2 , {\mathcal F}_1 \boxtimes {\mathcal F}_2, F_{12}{}) $が存在する. \begin{align*} {\mathsf O}_{12}^{(1)}={\mathsf O}_1, \qquad {\mathsf O}_{12}^{(2)} ={\mathsf O}_2 \end{align*}
また,このとき,${\mathsf O}_{12}$は一意に決まる.
証明: 証明は, たとえば、 "S. Ishikawa, "Mathematical Foundations of measurement theory,Keio University Press Inc. 2006を見よ。