8.2: 擬積観測量の制約条件
測定
${\mathsf M}_{\overline{\mathcal A}} (
{\mathsf O}_{12}
{{=}}
(
X_1 \times X_2,
{\cal F}_1 \boxtimes {\cal F}_2,
F_{12}{}),
S_{[\rho]})$
は,
サンプル空間
$
(
X_1 \times X_2,
{\cal F}_1 \boxtimes {\cal F}_2,
{}_{{\mathcal A}^*} \big(\rho,
{}F_{12} (\cdot ) {}\big) {}_{\overline{\mathcal A} }
)$
を持つとする.
このサンプル空間の別表現を,以下のように表現する.
\begin{align*}
{\mbox{Rep}}_\rho^{\Xi_1\times \Xi_2}[{}{\mathsf O}_{12}]
=
\left[\begin{array}{ll}
{}_{{\mathcal A}^*} \big(\rho,
{}F_{12} (\Xi_1 \times \Xi_2{}) {}\big) {}_{\overline{\mathcal A} }
&
{}_{{\mathcal A}^*} \big(\rho,
{}F_{12} (\Xi_1 \times \Xi_2^c{}) {}\big) {}_{\overline{\mathcal A} }
\\
{}_{{\mathcal A}^*} \big(\rho,
{}F_{12} (\Xi_1^c \times \Xi_2{}) {}\big) {}_{\overline{\mathcal A} }
&
{}_{{\mathcal A}^*} \big(\rho,
{}F_{12} (\Xi_1^c \times \Xi_2^c{}) {}\big) {}_{\overline{\mathcal A} }
\end{array}\right]
\quad
(\forall \Xi_1 \in {\mathcal F}_1, \forall \Xi_2
\in {\mathcal F}_2)
\end{align*}
と表す.
ここに,
$\Xi^c$
は
$\Xi$
の
補集合$\{ x \in X \;|\; x \notin \Xi \}$とする.
また,
証明
証明は簡単であるが,念の為に以下に書く.
$ 0 {{\; \leqq \;}}$
$ \rho( {}F (( \Xi'_1 \times \Xi'_2) {}{}) {}) $
$ {{\; \leqq \;}}1$,
$(\forall \Xi'_1
\in {\cal F}_1,
\Xi'_2 \in {\cal F}_2
)$
であるから,
(8.2)式から,次を得る:
\begin{align*}
&
0 {{\; \leqq \;}}\alpha^{{}^{\Xi_1 \times \Xi_2}}_\rho {{\; \leqq \;}}1
\\
&
0
{{\; \leqq \;}}
1+ \alpha^{{}^{\Xi_1 \times \Xi_2}}_\rho
-
\rho( {}F_1 ( \Xi_{1} {}{}) {})
-
\rho( {}F_2 ( \Xi_{2} {}{}) {})
{{\; \leqq \;}}1
\\
&
0 {{\; \leqq \;}}
\rho( {}F_2 ( \Xi_{2} {}{}) {})
- \alpha^{{}^{\Xi_1 \times \Xi_2}}_\rho
{{\; \leqq \;}}1
\\
&
0 {{\; \leqq \;}}
\rho( {}F_1 ( \Xi_{1} {}{}) {})
- \alpha^{{}^{\Xi_1 \times \Xi_2}}_\rho
{{\; \leqq \;}}1
\end{align*}
これから,(8.3)は容易にわかる.
逆に,
もし
$\alpha^{{}^{\Xi_1 \times \Xi_2}}_\rho$
が条件(8.3)を満たすならば,
(8.2)は
直ちにわかる.
また,
(8.4)も自明である.
さて,
${\mathsf O}_{1}$
${{=}}$
$(
X_1,
{\cal F}_1 ,
F_{1}{})$
と
${\mathsf O}_{2}$
${{=}}$
$(
X_2,
{\cal F}_2 ,
F_{2}{} )$
を
$\overline{\mathcal A}$
内の
観測量として,
${\mathsf O}_{12}$
${{=}}$
$(
X_1 \times X_2,
{\mathcal F}_1 \boxtimes {\mathcal F}_2,
F_{12}{}{{=}} F_1
\mathop{\times}^{qp}
F_2)$
を
${\mathsf O}_{1}$
と
${\mathsf O}_{2}$
の擬積観測量とする.
ここで,
測定
${\mathsf M}_{\overline{\mathcal A}} ({\mathsf O}_{12} $
${{=}}(X_1 \times X_2,
{\cal F}_1 \boxtimes {\cal F}_2,
F_{12}{}{{=}} F_1
{\mathop{\times}^{qp}}
F_2),$
$ S_{[\rho]})$)
により,
測定値$(x_1, x_2)$
$(\in X_1 \times X_2 )$
が得られたとする.
このとき,
$x_1 \in \Xi_1$
であることを
知ったとき,
$x_2 \in \Xi_2$
である確率$P$
(すなわち,
条件付き確率
)は
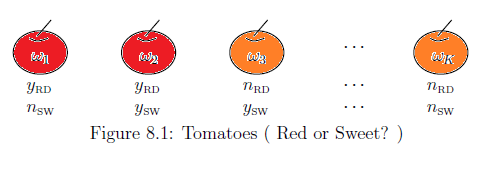
例 8.5 [例: トマト]
$\Omega$
$ = $
$ \{ \omega_1 , \omega_2 ,\ldots\omega_k,\ldots, \omega_K \}$
を$K$個のトマト
の集合とする.
古典系の基本構造
\color{red}
\begin{align*}
[C_0(\Omega ) \subseteq L^\infty ( \Omega, \nu ) \subseteq B(L^2 ( \Omega, \nu ))]
\end{align*}
\color{black}
を設定する.
ここで,
同一視
「トマト$\omega_k$
$\longleftrightarrow$
状態$\delta_{\omega_k} \approx \omega_k \in \Omega$をもつトマト」
を考える.
$L^\infty (\Omega {})$
内の
観測量
${\mathsf O}_{{{}_{RD}}}$
${{=}}$
$(X_{{}_{RD}} , 2^{ X_{{}_{RD}} } , F_{{}_{RD}}{})$
と
${\mathsf O}_{{}_{SW}}$
${{=}}$
$(X_{{}_{SW}} , 2^{ X_{{}_{SW}} } , F_{{}_{SW}}{})$
を考えよう.ここに,
\begin{align*}
X_{{}_{RD}}
=
\{ y_{{}_{RD}} , n_{{}_{RD}} \}
,
\qquad
X_{{}_{SW}}
=
\{ y_{{}_{SW}} , n_{{}_{SW}} \}
\end{align*}
で,
"$y_{{}_{RD}}$"
と
"$n_{{}_{RD}}$"
はそれぞれ
"赤い"
と
"赤くない"
を意味する.
同様に,
"$y_{{}_{SW}}$"
と
"$n_{{}_{SW}}$"
はそれぞれ
"甘い"
と
"甘くない"
を意味するとしよう.
たとえば,
「トマト$\omega_1$は赤いけど甘くない」
や「トマト$\omega_2$は赤くて,しかも甘い」
などの文言を考える.
次の擬積観測量
を考える:
であり,
$[{}F (\{(y_{{}_{RD}} , y_{{}_{SW}}{}) \}{}){}]({\omega_k}{})=
\alpha^{{}^{\{(y_{{}_{RD}} , y_{{}_{SW}}{}) \}}
}
(\omega_k)$であるから,
条件付確率$P$の評価:
\begin{align*}
&
{}_{{\mathcal A}^*} \big(\rho,
{}F_{12} (\Xi_1 \times \Xi_2{}) {}\big) {}_{\overline{\mathcal A} }
+
{}_{{\mathcal A}^*} \big(\rho,
{}F_{12} (\Xi_1 \times \Xi_2^c{}) {}\big) {}_{\overline{\mathcal A} }
=
{}_{{\mathcal A}^*} \big(\rho,
{}F_{12}^{(1)}] (\Xi_1 {}) {}\big) {}_{\overline{\mathcal A} }
\\
&
{}_{{\mathcal A}^*} \big(\rho,
{}F_{12} (\Xi_1^c \times \Xi_2^c{}) {}\big) {}_{\overline{\mathcal A} }
+
{}_{{\mathcal A}^*} \big(\rho,
{}F_{12} (\Xi_1^c \times \Xi_2{}) {}\big) {}_{\overline{\mathcal A} }
=
{}_{{\mathcal A}^*} \big(\rho,
{}F_{12}^{(1)} (\Xi_1^c {}) {}\big) {}_{\overline{\mathcal A} }
\\
&
{}_{{\mathcal A}^*} \big(\rho,
{}F_{12} (\Xi_1^c \times \Xi_2^c{}) {}\big) {}_{\overline{\mathcal A} }
+
{}_{{\mathcal A}^*} \big(\rho,
{}F_{12} (\Xi_1 \times \Xi_2^c{}) {}\big) {}_{\overline{\mathcal A} }
=
{}_{{\mathcal A}^*} \big(\rho,
{}F_{12}^{(2)} (\Xi_2^c {}) {}\big) {}_{\overline{\mathcal A} }
\\
&
{}_{{\mathcal A}^*}\big(\rho,
{}F_{12} (\Xi_1 \times \Xi_2^c{}) {}\big) {}_{\overline{\mathcal A} }
+
{}_{{\mathcal A}^*} \big(\rho,
{}F_{12} (\Xi_1^c \times \Xi_2^c{}) {}\big) {}_{\overline{\mathcal A} }
=
{}_{{\mathcal A}^*} \big(\rho,
{}F_{12}^{(2)} (\Xi_2^c {}) {}\big) {}_{\overline{\mathcal A} }
\end{align*}
に注意せよ.
次の補題で,
擬積観測量
が満たすべき条件
を示す.
補題8.4 [擬積観測量の制約条件]
基本構造$[ {\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]$
を考える.
${\mathsf O}_{1}$
${{=}}$
$(
X_1,
{\cal F}_1 ,
F_{1}{})$
と
${\mathsf O}_{2}$
${{=}}$
$(
X_2,
{\cal F}_2 ,
F_{2}{} )$
を
$\overline{\mathcal A}$
内の
観測量とする.
${\mathsf O}_{12}$
${{=}}$
$(
X_1 \times X_2,
{\cal F}_1 \boxtimes {\cal F}_2,
F_{12}{}{{=}} F_1
\mathop{\times^{qp}}
F_2
)$
を
${\mathsf O}_{1}$
と
${\mathsf O}_{2}$
の擬積観測量とする(存在は仮定する).
すなわち,
\begin{align*}
F_1 = F_{12}^{(1)},
\qquad
F_2= F_{12}^{(2)}
\end{align*}
とする.
測定
${\mathsf M}_{\overline{\mathcal A}} (
{\mathsf O}_{12}
{{=}}
(
X_1 \times X_2,
{\cal F}_1 \boxtimes {\cal F}_2,
F_{12}{}),
S_{[\rho]})$
は,
サンプル空間
$
(
X_1 \times X_2,
{\cal F}_1 \boxtimes {\cal F}_2,
{}_{{\mathcal A}^*} \big(\rho,
{}F_{12} (\cdot ) {}\big) {}_{\overline{\mathcal A} }
)$
を持つとする.
このとき,
$\alpha^{{}^{\Xi_1 \times \Xi_2}}_\rho
=
{}_{{\mathcal A}^*} \big(\rho,
{}F_{12} (\Xi_1 \times \Xi_2{}) {}\big) {}_{\overline{\mathcal A} }
=
\rho(F_{12} (\Xi_1 \times \Xi_2{}))
$
とおいて,
\begin{align}
&
\; \;
{\rm{Rep}}_\rho^{\Xi_1\times \Xi_2}[{\mathsf O}_{12}]
=
\left[\begin{array}
_{{\mathcal A}^*} \big(\rho,
F_{12} (\Xi_1 \times \Xi_2) \big) _{\overline{\mathcal A} }
&
_{{\mathcal A}^*} \big(\rho,
F_{12} (\Xi_1 \times \Xi_2^c) \big) _{\overline{\mathcal A} }
\\
_{{\mathcal A}^*} \big(\rho,
F_{12} (\Xi_1^c \times \Xi_2) \big) _{\overline{\mathcal A} }
&
_{{\mathcal A}^*} \big( \rho,
F_{12} (\Xi_1^c \times \Xi_2^c) \big) _{\overline{\mathcal A} }
\end{array}\right]
\nonumber
\\
=
&
\left[\begin{array}{ll}
\alpha^{^{\Xi_1 \times \Xi_2}}_\rho
&
\rho( F_1 (\Xi_1)) - \alpha^{^{\Xi_1 \times \Xi_2}}_\rho
\\
\rho( F_2 (\Xi_2))- \alpha^{^{\Xi_1 \times \Xi_2}}_\rho
&
1+ \alpha^{^{\Xi_1 \times \Xi_2}}_\rho -
\rho( F_1 (\Xi_1)) -
\rho( F_2 (\Xi_2))
\end{array}\right]
\tag{8.2}
\end{align}
かつ,
次が成立する:
\begin{align}
&
\max \{
0,
\rho( {}F_1 (\Xi_1))+
\rho( {}F_2 (\Xi_2))
-1
{}
\}
{{\; \leqq \;}}
\alpha^{{}^{\Xi_1 \times \Xi_2}}_\rho
{{\; \leqq \;}}
\nonumber
\\
&
\min
\{
\rho( {}F_1 (\Xi_1))
,
\;
\rho( {}F_2 (\Xi_2))
\}
\nonumber
\\
&
(\forall \Xi_1 \in {\cal F}_1,
\forall \Xi_2 \in {\cal F}_2,
\forall \rho \in {\frak S}^p({\mathcal A}^*) )
\tag{8.3}
\end{align}
また, 次が成り立つ:
\begin{align}
\rho( {}F {}( \Xi_{1} \times \Xi^c_{2}{}) {}{} {})
=0
\;
& \Longleftrightarrow
\;
\alpha^{{}^{\Xi_1 \times \Xi_2}}_\rho =
\rho( {}F_1 ( \Xi_{1} {}{}) {})
\nonumber
\\
&\Longrightarrow
\;
\rho( {}F_1 ( \Xi_{1} {}{}) {})
{{\; \leqq \;}}
\rho( {}F_2 ( \Xi_{2} {}{}) {})
\tag{8.4}
\end{align}
ここに,
$\alpha_{\omega_k}^{{}^{\{( y_{{{}_{RD}}} , y_{{{}_{SW}}}{}) \} }} ({\omega_k})$
は(8.3)を満たす.
したがって,
トマト
${\omega_k} $
が「赤い」
とわかったとき,
そのトマト
${\omega_k} $
が
「甘い」ことがわかる確率$P$は
8.2: 擬積観測量の制約条件
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
$\square \quad$
