8.3.1: 含意、　対偶

例 8.5の続きとして、 $[F (\{( y_{_{RD}} , n_{_{SW}}) \}) ] (\omega)=0$の場合について考えよう。

\begin{align} \frac{ [F (\{(y_{_{RD}} , y_{_{SW}}) \})](\omega) } { [F (\{(y_{_{RD}} , y_{_{SW}}) \})](\omega) + [F (\{(y_{_{RD}} , n_{_{SW}}) \})](\omega) } =1 \end{align}

であるから， トマト $\omega $ が「赤い」 とわかったとき， そのトマト $\omega $ が 「甘い」ことがわかる確率は $1$となる． すなわち，

\begin{align} \mbox{" $[F (\{( y_{_{RD}} , n_{_{SW}}) \}) ] (\omega) = 0$"} \quad \Longleftrightarrow \quad \Big[ \mbox{" Red"} \Longrightarrow \mbox{" Sweet"} \Big] \end{align}

上の議論から， 次の定義 「含意($\Rightarrow$)」 (すなわち， 「測定理論的含意」， 「二元論的含意」) を得る：

定義8.6 [含意] 基本構造 \begin{align*} [ {\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)] \end{align*} 内で考える. ${\mathsf O}_{12}$ $=$ $(X_1 \times X_2 ,$ $ {\cal F}_1 \boxtimes {\cal F}_2 ,$ $ F_{12}{}{{=}} F_1 {\mathop{\times}^{qp}} F_2)$ を ${{\overline{\mathcal A}}}$ 内の 観測量 とする． $\rho \in {\frak S}^p({\mathcal A}^* ) $， $\Xi_1$ $ \in {\cal F}_1 $， $\Xi_2$ $ \in {\cal F}_2$ とする． ここで， \begin{align*} \rho(F{}_{12}{} (\Xi_1 \times ( \Xi^c_2{}){})) = 0 \end{align*} が成立するとき, \begin{align} [{\mathsf O}_{12}^{(1)};{\Xi_1}] \underset{ {\mathsf M}_{{\overline{\mathcal A}}} ({\mathsf O}_{12} , S_{ [\rho] }{}) }{ \Longrightarrow} [{\mathsf O}_{12}^{(2)};{\Xi_2}] \tag{8.5} \end{align} と書く．

もちろん， これを，

$(A):$ 測定${\mathsf M}_{{\overline{\mathcal A}}} ({\mathsf O}_{12} , S_{ [\rho] }{})$ により， 測定値 $(x_1, x_2) (\in X_1 \times X_2)$ が得られたとする． このとき， $x_1 \in \Xi_1$ ならば $x_2 \in \Xi_2$ である．

と読む． これは次のように一般化できる． 基本構造$[ {\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)]$ 内の 観測量 ${\mathsf O}_{12...n}$ ${{=}}$ $({{{\times}}}_{k=1}^n X_k ,$ $ \boxtimes_{k=1}^n{\cal F}_k , $ ${F}_{12...n} = \underset{k=1,2,...,n}{\mathop{\times}^{qp}} F_k {})$ を考える． また， $\rho \in {\frak S}^p({\mathcal A}^*) $, $\Xi_i$ $ \in {\cal F}_i $， $\Xi_j$ $ \in {\cal F}_j$ として($1{{\; \leqq \;}}i , j {{\; \leqq \;}}n$)， ここで，

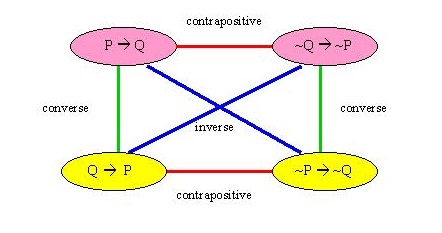
\begin{align*} {}_{{\mathcal A}^*} \big(\rho, {F}^{(ij)}_{12...n} (\Xi_i \times ( \Xi^c_j{}){}) \big) {}_{\overline{\mathcal A} } = 0 \end{align*} (ここに, $\Xi^c$は$\Xi$の補集合) が成立するとき, \begin{align} [{\mathsf O}_{12...n}^{(i)};{\Xi_i}] \underset{ {\mathsf M}_{{\overline{\mathcal A}}} ({\mathsf O}_{12...n} , S_{ [\rho] }{}) }{ \Longrightarrow} [{\mathsf O}_{12...n}^{(j)};{\Xi_j}] \tag{8.6} \end{align} と書く．

定理 8.7 [対偶] ${\mathsf O}_{12}$ $=$ $(X_1 \times X_2 ,$ $ {\cal F}_1 \boxtimes {\cal F}_2 ,$ $ F_{12}{}{{=}} F_1 {\mathop{\times}^{qp}} F_2)$ を ${{\overline{\mathcal A}}}$ 内の 観測量 とする． $\rho \in {\frak S}^p({\mathcal A}^*) $ とする． $\Xi_1$ $ \in {\cal F}_1 $ と $\Xi_2$ $ \in {\cal F}_2$ を考える．このとき， \begin{align} [{\mathsf O}_{12}^{(1)};{\Xi_1}] \underset{ {\mathsf M}_{{\overline{\mathcal A}}} ({\mathsf O}_{12} , S_{ [\rho] }{}) }{ \Longrightarrow} [{\mathsf O}_{12}^{(2)};{\Xi_2}] \tag{8.7} \end{align} ならば， \begin{align*} [{\mathsf O}_{12}^{(1)};{\Xi_1^c}] \underset{ {\mathsf M}_{{\overline{\mathcal A}}} ({\mathsf O}_{12} , S_{ [\rho] }{}) }{ \Longleftarrow} [{\mathsf O}_{12}^{(2)};{\Xi_2^c}] \end{align*}

証明$\;\;$ 証明は自明であるが，念の為，証明を加える． 条件 (8.7)を仮定しよう． すなわち， \begin{align*} {}_{{\mathcal A}^*} \big(\rho, F_{12}{} (\Xi_1 \times (X_2 \setminus \Xi_2{}){}) \big) {}_{\overline{\mathcal A} } = 0 \end{align*} ここで， $\Xi_1 \times \Xi_2{}^c = (\Xi_1^c)^c \times \Xi_2^c $ だから， \begin{align*} {}_{{\mathcal A}^*} \big(\rho, F_{12}{} ( (\Xi_1^c)^c \times \Xi_2^c{}) \big) {}_{\overline{\mathcal A} } = 0 \end{align*} よって， \begin{align*} [{\mathsf O}_{12}^{(1)};{\Xi_1^c}] \underset{ {\mathsf M}_{{\overline{\mathcal A}}} ({\mathsf O}_{12} , S_{ [\rho] }{}) }{ \Longleftarrow} [{\mathsf O}_{12}^{(2)};{\Xi_2^c}] \end{align*} を得る．

$\square \quad$