8.4: Cogito --- I think, therefore I am---
以下の例は,すこし不自然かもしれないが,
「二元論」の理解のためには
欠かせない .
例 8.8 [脳死]
古典系の基本構造
\begin{align*}
[C_0(\Omega ) \subseteq L^\infty ( \Omega, \nu ) \subseteq B(L^2 ( \Omega, \nu ))]
\end{align*}
を設定する.
太郎君を測定対象とする.
太郎君の状態を
$\omega_1$,
$\omega_2$,....,$\omega_N$
のいずれかと
する.
すなわち,状態空間を
$\Omega=\{\omega_1,\omega_2,\ldots, \omega_N \}$
とする.
${\mathsf O}_{12}$
$=$
$(X_1 \times X_2 ,$
$ 2^{ X_1 \times X_2 } ,$
$ F_{12}{}{{=}} F_1
{\mathop{\times}^{qp}}
F_2)$
を${L^\infty (\Omega)}$
内の
観測量
とする.
ここに,
$X_1=\{ 思, {\overline 思}\}$,
$X_2=\{ 生, {\overline 生}\}$
とする.
もちろん,
「思」=「思う」,
「${\overline 思}$」=「思わない」
等とする.
また,
任意の状態$\omega_n$
$(n=1,2,\ldots,N)$に対して,
表8.1
を満たすとする.
上の(A$_1$)と次の「デカルト命題(コギト命題)(A$_2$)」とを混同してはならない。
しかし、量子言語では、
「観客は舞台に上がってはならない」
なので、

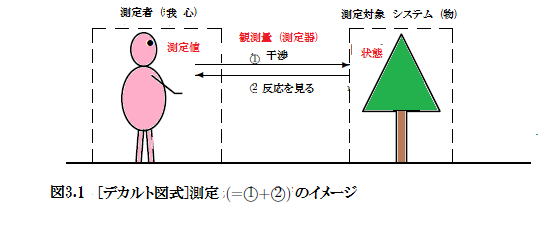
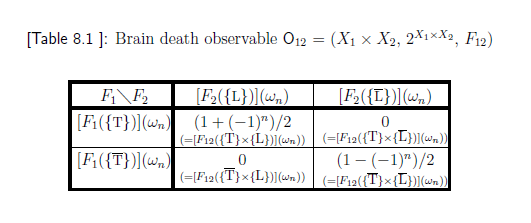
このとき,
明らかに,
次が成立する:
\begin{align*}
[{\mathsf O}_{12}^{(1)};{
\{
{\text{ 思}}
\}
}]
\underset{ {\mathsf M}_{C (\Omega)} ({\mathsf O}_{12} ,
S_{ [\omega_n] }{}) }{ \Longleftrightarrow}
[{\mathsf O}_{12}^{(2)};{\{
{{\text{ 生}}}
\}}]
\end{align*}
もちろん,
これを,
$(A_1):$
太郎君が「思って」いることがわかれば,「生きて」いることがわかる.
逆に,
「生きて」いることがわかれば,
「思って」いることがわかる.
 と読む.すなわち,「脳死」のことを言っていると思ってよい.
と読む.すなわち,「脳死」のことを言っていると思ってよい.
次の対応の下に、コギト命題(A$_2$)は主張されている:
$(A_2):$
"我考える, 故に、我あり"
$\quad$
$\qquad$
測定者$\longleftrightarrow$我,
$\qquad$
システム$\longleftrightarrow$我

したがって、 コギト命題(A$_2$) は 二元論の命題 (=量子言語の命題) ではない。 図 8.2(i.e., 二元論)を提唱するするために (すなわち、 「我」を確立するために), デカルトは あいまいな コギト命題(A$_2$) からスタートした。 次のような皮肉な言い方で、まとめると、
| $(B):$ | 二元論的でないコギト命題(A$_2$)によって、 デカルトは 二元論 (i.e., 図8.2) を提唱した |
要約すると、 コギト命題は
- 「『我(=測定者)』の発見」の宣言
- 「『二元論(=デカルト図式)』の発見」の宣言
念の為、補足すると、 コギト命題は、「疑う余地が全くない真理」というわけでばかりか、量子言語では記述できない怪しい命題である。 しかし、コギト命題から初めて、強引な荒業で、すなわち、
- 理屈を無視した、心理的手品で
「我の存在(=二元論の確立)」を主張するのがデカルトの戦術で、 これは大成功した。
| $\fbox{注釈8.1}$ |
世界記述法を前提にしなで、「疑う余地が全くない真理」に嵌ってしまうのは、一種の中二病であるが、
この世界のすべての現象が測定理論で記述できるわけではないことは当然で,
しかも,量子言語で記述できなくても「重要なこと」など幾らでもある.
「書けそうで,書けないもの」としては,
たとえば,
なのだから,①--⑧の言葉を記述したければ, 量子言語とは別の言語を提案しなければならない. 事実、⑧を記述するためにアインシュタインは、相対性理論という言語を提案した。
とも言える。 |
