結合観測量 -- 測定は一回だけ

8.5: 結合観測量 ---測定は一回だけ

言語的解釈に従うなら、 \begin{align} & \mbox{"測定は一回だけ"} \\ & \Rightarrow \mbox{ "観測量は一つだけ"} \Rightarrow \mbox{ "結合観測量"} \end{align} という道筋は、一理ある。　この節では、これについて述べる。次の定理を準備する。

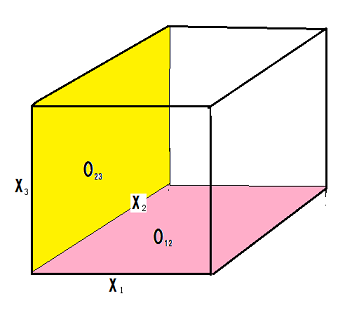定理8.9 [古典結合観測量の存在定理] 古典系の基本構造 \begin{align*} [C_0(\Omega ) \subseteq L^\infty ( \Omega, \nu ) \subseteq B(L^2 ( \Omega, \nu ))] \end{align*}

内で,観測量 ${\mathsf O}_{12}{{=}} (X_1 \times X_2 , {\mathcal F}_1 \boxtimes {\cal F}_2, F_{12})$ と ${\mathsf O}_{23}{{=}} $ $(X_2 \times X_3 ,$ $ {\mathcal F}_2 \boxtimes {\mathcal F}_3, F_{23})$ を考える．ただし，ここに $X_i{{=}} \{x^1_i, x^2_i,\ldots, x^{n_i}_i\}$ $(i=1,2,3)$ は有限集合， ${\mathcal F}_i = 2^{X_i}$ とする．次を仮定する:

\begin{align*} {\mathsf O}_{12}^{(2)} = {\mathsf O}_{23}^{(2)} \quad (\text{すなわち，}\;\; F_{12}(X_1 \times \Xi_2 ) = F_{23}(\Xi_2 \times X_3 ) \quad(\forall \Xi_2 \in 2^{X_2})) \end{align*}

このとき，次を満たす$L^\infty (\Omega)$内の観測量 ${\mathsf O}_{123}{{=}} (X_1 \times X_2 \times X_3, {\mathcal F}_1 \boxtimes {\mathcal F}_2 \boxtimes {\mathcal F}_3, F_{123})$ が存在する:

\begin{align*} {\mathsf O}_{123}^{(12)} = {\mathsf O}_{12}, \quad {\mathsf O}_{123}^{(23)} = {\mathsf O}_{23} \end{align*} すなわち， \begin{align} F_{123}^{(12)}(\Xi_1 \times \Xi_2 \times X_3) & = F_{12}(\Xi_1 \times \Xi_2 ),\;\; F_{123}^{(23)}(X_1 \times \Xi_2 \times \Xi_3 ) = F_{23}(\Xi_2 \times \Xi_3 ) \nonumber \\ & \quad(\forall \Xi_1 \in {\mathcal F}_1, \forall \Xi_2 \in {\mathcal F}_2, \forall \Xi_3 \in {\mathcal F}_3 )) \tag{8.8} \end{align}

である．この ${\mathsf O}_{123}$を ${\mathsf O}_{12}$と${\mathsf O}_{23}$ の 結合観測量 と呼ぶ．

証明観測量${\mathsf O}_{123}$ $=$ $(X_1 \times X_2 \times X_{3} , $ ${ {\mathcal F}_1 \times {\mathcal F}_{2} \times {\mathcal F}_3}, $ $F_{123})$ を次のように定義する：

\begin{align} & \; \; [F_{123} (\{(x_{1} , x_{2} , x_{3}　) \}) ] (\omega) \\ & = \left\{\begin{array}{ll} {\displaystyle \frac{ [F_{12} (\{(x_{1} , x_{2}) \})] (\omega) \cdot [F_{23} (\{(x_{2} , x_{3}) \})] (\omega) } { [F_{12} (X_1 \times \{ x_{2} \})] (\omega) } } \\ & ( [F_{12} (X_1 \times \{ x_{2} \})] (\omega) \; \not= 0\mbox{のとき}) \\ \\ 0 \\ & ( [F_{12} (X_1 \times \{ x_{2} \})] (\omega) = 0\mbox{のとき}) \\ \end{array}\right. \\ & \qquad \qquad \qquad (\forall \omega \in \Omega, \forall (x_1,x_2,x_3) \in X_1 \times X_2 \times X_3) \end{align} この観測量は明らかに(8.8)を満たす.

$\square \quad$

反例8.10 [量子システムでの反例] 上の定理は, 量子系の基本構造 \begin{align*} [{\mathcal C}(H) \subseteq B(H) \subseteq B(H)] \end{align*} 内では成立しない.これを確認するためには,ヒルベルト空間 $H={\mathbb C}^n$を考えて, 三つの$(n \times n)$-エルミート行列 $T_1$, $T_2$, $T_3$を \begin{align} T_1 T_2 =T_2 T_1, \quad T_2 T_3 =T_3 T_2, \quad T_1 T_3 \not= T_3 T_1 \tag{8.9} \end{align} と選べばよい. $X_k ={\mathbb R}, {\mathcal F}_k={\mathcal B}_{\mathbb R}$ $(k=1,2,3)$とおいて, エルミート行列$T_k$のスペクトル分解を射影観測量 ${\mathsf O}_k=(X_k, {\mathcal F}_k, F_k )$とする.　すなわち, \begin{align} T_k = \int_{X_k} x_k F_k ( d x_k ) \tag{8.10} \end{align} とする.可換性から, 二つの同時射影観測量 \begin{align} & {\mathsf O}_{12}{{=}} {\mathsf O}_1 \times {\mathsf O}_2 =(X_1 \times X_2 , {\mathcal F}_1 \boxtimes {\mathcal F}_2, F_{12}=F_1 \times F_2) \nonumber \end{align} と \begin{align} & {\mathsf O}_{23}{{=}} {\mathsf O}_2 \times {\mathsf O}_3= (X_2 \times X_3 , {\mathcal F}_2 \boxtimes {\mathcal F}_3, F_{23}=F_2 \times F_3) \end{align} を考える．

当然 \begin{align*} {\mathsf O}_{12}^{(2)} = {\mathsf O}_{23}^{(2)} \quad (\text{すなわち，}\;\; F_{12}(X_1 \times \Xi_2 ) =F_2(\Xi_2 ) = F_{23}(\Xi_2 \times X_3 ) \quad(\forall \Xi_2 \in {\mathcal F}_2)) \end{align*} が成り立つ. しかしながら, 次を満たす$B(H)$内の観測量 ${\mathsf O}_{123}{{=}} (X_1 \times X_2 \times X_3, {\mathcal F}_1 \boxtimes {\mathcal F}_2 \boxtimes {\mathcal F}_3, F_{123})$ が存在しない \begin{align*} {\mathsf O}_{123}^{(12)} = {\mathsf O}_{12}, \quad {\mathsf O}_{123}^{(23)} = {\mathsf O}_{23} \end{align*}

なぜならば, このような${\mathsf O}_{123}$が存在したら, 定理8.3から,${\mathsf O}_1$と${\mathsf O}_3$が可換になってしまい,　それは,式(8.9)の $T_1 T_3 \not= T_3 T_1$に矛盾してしまうからである. したがって， ${\mathsf O}_{12}$と${\mathsf O}_{23}$ の 結合観測量 ${\mathsf O}_{123}$は存在しない.

8.5.2: 結合観測量とベルの不等式：再考

このとき次の問題を考える:

問題8.11 [結合観測量とベルの不等式 ] 基本構造 \begin{align*}[ {\mathcal A} \subseteq \overline{\mathcal A} \subseteq B(H)] \end{align*} を考える.すなわち,古典系でも量子系でもどちらでも構わない. $X_1=X_2=X_3=X_4=\{-1, 1\}$ とする． ${\mathsf O}_{13}{{=}} (X_1 \times X_3 , 2^{X_1} \times 2^{X_3} , F_{13})$， ${\mathsf O}_{14}{{=}} (X_1 \times X_4 , 2^{X_1} \times 2^{X_4} , F_{14})$， ${\mathsf O}_{23}{{=}} $ $(X_2 \times X_3 ,$ $ 2^{X_2} \boxtimes 2^{X_3} , F_{23})$ と ${\mathsf O}_{24}{{=}} $ $(X_2 \times X_3 ,$ $ 2^{X_2} \boxtimes 2^{X_4} , F_{24})$ を $\overline{\mathcal A}$内の観測量とする．ここで，次を仮定する: \begin{align*} {\mathsf O}_{13}^{(1)}={\mathsf O}_{14}^{(1)}, \;\; {\mathsf O}_{23}^{(2)}={\mathsf O}_{24}^{(2)}, \;\; {\mathsf O}_{13}^{(3)}={\mathsf O}_{23}^{(3)}, \;\; {\mathsf O}_{14}^{(4)}={\mathsf O}_{24}^{(4)} \end{align*} 更に， $\{-1, 1 \}^2$上の確率測度$\nu_{ab}$を (4.49) 式 (in $\S$4.5: ベルの不等式) で定めて，ある状態$\rho_0 \in {\frak S}^p({\overline{\mathcal A}}) $ で \begin{align*} & \rho_0( F_{13}(\{(x_1,x_3)\}))=\nu_{a^1b^1}(\{(x_1,x_3)\}), \\ & \rho_0( F_{14}(\{(x_1,x_4)\}))=\nu_{a^1b^2}(\{(x_1,x_4)\}), \\ & \rho_0( F_{23}(\{(x_2,x_3)\}))=\nu_{a^2b^1}(\{(x_2,x_3)\}), \\ & \rho_0( F_{24}(\{(x_2,x_4)\}))=\nu_{a^2b^2}(\{(x_2,x_4)\}), \end{align*} を満たすと仮定する．
このとき次の問題を考える:

$\overline{\mathcal A}$内の観測量${\mathsf O}_{1234}{{=}} ({{{\times}}}_{k=1}^4 X_k , \boxtimes_{k=1}^4{\mathcal F}_k , F_{1234})$ で次の($\sharp$)を満たすものが存在するか？

$(\sharp):$

$ \displaystyle {\mathsf O}_{1234}^{(13)} = {\mathsf O}_{13}, \;\; {\mathsf O}_{1234}^{(14)} = {\mathsf O}_{14}, \;\; {\mathsf O}_{1234}^{(23)} = {\mathsf O}_{23}, \;\; {\mathsf O}_{1234}^{(24)} = {\mathsf O}_{24} \;\; $

この答えは，「このような${\mathsf O}_{1234}$ は存在しない」であるが，以下にこれを示そう．

解答.

${\mathsf O}_{1234}{{=}} ({{{\times}}}_{k=1}^4 X_k , $ $ \boxtimes_{k=1}^4{\mathcal F}_k ,$ $ F_{1234})$ が存在すると仮定して，矛盾を示せばいい． $C_{13}(\omega_0)$等を以下のように定める． \begin{align*} & C_{13}(\rho_0) = \int_{{{{\times}}}_{k=1}^4 X_k} x_1 \cdot x_3 \; [F_{1234}({{{\times}}}_{k=1}^4 dx_k )](\rho_0) \\ & \bigl( = \int_{X_1 \times X_3} x_1 \cdot x_3 \; \nu_{a^1 b^1} ( dx_1 dx_3) \bigl) \\ & C_{14}(\rho_0) = \int_{{{{\times}}}_{k=1}^4 X_k} x_1 \cdot x_4 \; [F_{1234}({{{\times}}}_{k=1}^4 dx_k )](\rho_0) \\ & \bigl(= \int_{X_1 \times X_4} x_1 \cdot x_4 \; \nu_{a^1b^2}( dx_1dx_4) \bigl) \\ & \displaystyle C_{23}(\rho_0) = \int_{{{{\times}}}_{k=1}^4 X_k} x_2 \cdot x_3 \; [F_{1234}({{{\times}}}_{k=1}^4 dx_k )](\rho_0) \\ & \bigl(= \int_{X_2 \times X_3} x_2 \cdot x_3 \; \nu_{a^2b^1}( dx_2dx_3) \bigl) \\ & C_{24}(\rho_0) = \int_{{{{\times}}}_{k=1}^4 X_k} x_2 \cdot x_4 \; [F_{1234}({{{\times}}}_{k=1}^4 dx_k )](\rho_0) \\ & \bigl(= \int_{X_2 \times X_4} x_2 \cdot x_4 \; \nu_{a^2b^2}( dx_2dx_4) \bigl) \end{align*} ここで，次の不等式(ベルの不等式)を(定理4.17($\S$4.5) を使うまでもなく)容易に求めることができる \begin{align} & |C_{13}(\rho_0)-C_{14}(\rho_0)| + |C_{23}(\rho_0)+C_{24}(\rho_0)| \nonumber \\ {{\; \leqq \;}} & \int_{{{{\times}}}_{k=1}^4 X_k} \!\!\! | x_1 | \cdot |x_3-x_4| \;\;+ \!\! |x_2 | \cdot |x_3+x_4| \big[F_{1234}({{{\times}}}_{k=1}^4 dx_k )\big](\rho_0) \nonumber \\ {{\; \leqq \;}} & 2 \qquad (\text{なぜならば，} x_k \in \{-1, 1\} ) \tag{8.11} \end{align}

しかし，これは， $\nu_{ab}$の方での計算では，すなわち， (4.51) 式では$2{\sqrt 2}$ であった．したがって，矛盾が生じるので，問題8.11のような ${\mathsf O}_{1234}$ は存在しない．もちろん，

$(b):$

並行測定 ${\mathsf M}_{C( \Omega^4)} ( {\mathsf O}_{13} \otimes {\mathsf O}_{14} \otimes {\mathsf O}_{23} \otimes {\mathsf O}_{24} ,$ $ S_{[(\rho_0, \rho_0, \rho_0, \rho_0)]})$ を考えるならば($\nu_{ab}$の方の計算なので)， (4.51) 式のように $2{\sqrt 2}$になる.

と言える．

$\fbox{注釈8.2}$

上の議論では，測定理論(という世界記述法)内の問題8.11を解くために，数学のベルの不等式(定理4.17参照)が使われている．隠れた変数に関わるような大きな議論ではないが, ベルの不等式の使い方として面白いと考える.

8.5: 結合観測量 -- 測定は一回だけ