8.6:実践三段論法─ソクラテスは死ぬか？
8.6.1: 三段論法とその変則形: 古典システム



さて， 次に， 実践三段論法 ─ 含意(定義8.6)に 関する測定理論の定理 ─ を議論する．

$(\sharp):$ 量子系では， 定理8.9 (観測量の結合定理) が一般には成立しないので ( 反例8.10で示したように, 観測量を結合できないので)， 三段論法は一般には成立しない．これについては, 注意8.15で,再度述べる
しかし， 古典系では， 定理8.9 (結合観測量の結合定理) が成立するので， 以下の定理によって， 三段論法は信頼できる．



定理 8.12 [古典系における三段論法] ${\mathsf O}_{123}$ $=$ $(X_1 \times X_2 \times X_3,$ $ {\cal F}_1 \boxtimes {\cal F}_2 \boxtimes {\cal F}_3 ,$ $ F_{123}{}{{=}} {\mathop{\times}^{qp}}_{k=1,2,3} F_k)$ を ${L^\infty (\Omega)}$ 内の 観測量 とする． $\omega \in \Omega $， $\Xi_1$ $ \in {\cal F}_1$， $\Xi_2$ $ \in {\cal F}_2$， $\Xi_3$ $ \in {\cal F}_3$ とする． このとき，次の命題 (i) $\text{--}$ (iii) が成立する．



(i).(実践三段論法) \begin{align} [{\mathsf O}_{123}^{(1)};{\Xi_1}] \underset{ {\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{123} , S_{ [\omega] }) }{ \Longrightarrow} [{\mathsf O}_{123}^{(2)};{\Xi_2}] , \quad [{\mathsf O}_{123}^{(2)};{\Xi_2}] \underset{ {\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{123} , S_{ [\omega] }) }{ \Longrightarrow} [{\mathsf O}_{123}^{(3)};{\Xi_3}] \end{align} ならば、 \begin{align} & \; \; \rm{Rep}_\omega^{\Xi_1 \times \Xi_3}[{\mathsf O}^{(13)}_{123}] = \left[\begin{array} [F^{(13)}_{123} (\Xi_1 \times \Xi_3)] (\omega) & [F^{(13)}_{123} (\Xi_1 \times \Xi_3^c)] (\omega) \\ [F^{(13)}_{123} (\Xi_1^c \times \Xi_3)] (\omega) & [F^{(13)}_{123} (\Xi_1^c \times \Xi_3^c)] (\omega) \end{array}\right] \\ = & \left[\begin{array} [F^{(1)}_{123}(\Xi_1)](\omega) & 0 \\ [F^{(3)}_{123}(\Xi_3)](\omega) - [F^{(1)}_{123}(\Xi_1)](\omega) & 1- [F^{(3)}_{123}(\Xi_3)](\omega) \end{array}\right] \end{align} すなわち, \begin{align} [{\mathsf O}_{123}^{(1)};{\Xi_1}] \underset{ {\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{123} , S_{ [\omega] }) }{ \Longrightarrow} [{\mathsf O}_{123}^{(3)};{\Xi_3}] \tag{8.12} \end{align} が成り立つ。

(ii).(実践三段論法の変則形) \begin{align} [{\mathsf O}_{123}^{(1)};{\Xi_1}] \underset{ {\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{123} , S_{ [\omega] }) }{ \Longleftarrow} [{\mathsf O}_{123}^{(2)};{\Xi_2}] , \quad [{\mathsf O}_{123}^{(2)};{\Xi_2}] \underset{ {\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{123} , S_{ [\omega] }) }{ \Longrightarrow} [{\mathsf O}_{123}^{(3)};{\Xi_3}] \end{align} ならば \begin{align} & \; \; \rm{Rep}_\omega^{\Xi_1 \times \Xi_3}[{\mathsf O}^{(13)}_{123}] = \left[\begin{array} [F^{(13)}_{123} (\Xi_1 \times \Xi_3)] (\omega) & [F^{(13)}_{123} (\Xi_1 \times \Xi_3^c)] (\omega) \\ [F^{(13)}_{123} (\Xi_1^c \times \Xi_3)] (\omega) & [F^{(13)}_{123} (\Xi_1^c \times \Xi_3^c)] (\omega) \end{array}\right] \\ = & \left[\begin{array} \alpha_{_{\Xi_1 \times \Xi_3}} &\;\;\;\; [F^{(1)}_{123}(\Xi_1)](\omega)-\alpha_{_{\Xi_1 \times \Xi_3}} \\ [F^{(3)}_{123}(\Xi_3)](\omega)-\alpha_{_{\Xi_1 \times \Xi_3}} &\;\;\;\; 1-\alpha_{_{\Xi_1 \times \Xi_3}} - [F^{(1)}_{123}(\Xi_1)] - [F^{(3)}_{123}(\Xi_3)] \end{array}\right] \end{align} ここで \begin{align} & \max \{ [F^{(2)}_{123}(\Xi_2)](\omega), [F^{(1)}_{123}(\Xi_1)](\omega)+ [F^{(3)}_{123}(\Xi_3)](\omega) - 1 \} \nonumber \\ & {{\; \leqq \;}} \alpha_{_{\Xi_1 \times \Xi_3}} (\omega) {{\; \leqq \;}} \min \{ [F^{(1)}_{123}(\Xi_1)](\omega) , [F^{(3)}_{123}(\Xi_3)](\omega) \} \tag{8.13} \end{align}

(iii).(実践三段論法の変則形) \begin{align} [{\mathsf O}_{123}^{(1)};{\Xi_1}] \underset{ {\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{123} , S_{ [\omega] }) }{ \Longrightarrow} [{\mathsf O}_{123}^{(2)};{\Xi_2}] , \quad [{\mathsf O}_{123}^{(2)};{\Xi_2}] \underset{ {\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{123} , S_{ [\omega] }) }{ \Longleftarrow} [{\mathsf O}_{123}^{(3)};{\Xi_3}] \end{align} ならば \begin{align} & \; \; \rm{Rep}_\omega^{\Xi_1 \times \Xi_3}[{\mathsf O}^{(13)}_{123}] = \left[\begin{array} [F^{(13)}_{123} (\Xi_1 \times \Xi_3)] (\omega) & [F^{(13)}_{123} (\Xi_1 \times \Xi_3^c)] (\omega) \\ [F^{(13)}_{123} (\Xi_1^c \times \Xi_3)] (\omega) & [F^{(13)}_{123} (\Xi_1^c \times \Xi_3^c)] (\omega) \end{array}\right] \\ = & \left[\begin{array} \alpha_{_{\Xi_1 \times \Xi_3}} (\omega) &\;\;\;\; [F^{(1)}_{123}(\Xi_1)](\omega)-\alpha_{_{\Xi_1 \times \Xi_3}} (\omega) \\ [F^{(3)}_{123}(\Xi_3)](\omega)-\alpha_{_{\Xi_1 \times \Xi_3}} (\omega) &\;\;\;\; 1-\alpha_{_{\Xi_1 \times \Xi_3}} (\omega) - [F^{(1)}_{123}(\Xi_1)](\omega) - [F^{(3)}_{123}(\Xi_3)](\omega) \end{array}\right] \end{align} ここで \begin{align} & \max \{ 0 , [F^{(1)}_{123}(\Xi_1)](\omega) + [F^{(3)}_{123}(\Xi_3)](\omega) - [F^{(2)}_{123}(\Xi_2)](\omega) \} \\ & {{\; \leqq \;}} \alpha_{_{\Xi_1 \times \Xi_3}} (\omega) {{\; \leqq \;}} \min \{[F^{(1)}_{123}(\Xi_1)](\omega) , [F^{(3)}_{123}(\Xi_3)](\omega) \} \end{align}


[Proof (i)] $\;\;$ (i): 条件より, \begin{align} & 0= [F^{(12)}_{123}(\Xi_1 \times \Xi_2^c )](\omega) = [F_{123}(\Xi_1 \times \Xi_2^c \times \Xi_3 )](\omega) + [F_{123}(\Xi_1 \times \Xi_2^c \times \Xi_3^c )](\omega) \\ & 0= [F^{(23)}_{123}(\Xi_2 \times \Xi_3^c )](\omega) = [F_{123}(\Xi_1 \times \Xi_2 \times \Xi^c_3 )](\omega) + [F_{123}(\Xi_1^c \times \Xi_2 \times \Xi_3^c )](\omega) \end{align} したがって, \begin{align} & 0= [F_{123}(\Xi_1 \times \Xi_2^c \times \Xi_3 )](\omega) = [F_{123}(\Xi_1 \times \Xi_2^c \times \Xi_3^c )](\omega) \\ & 0= [F_{123}(\Xi_1 \times \Xi_2 \times \Xi^c_3 )](\omega) = [F_{123}(\Xi_1^c \times \Xi_2 \times \Xi_3^c )](\omega) \end{align} よって, \begin{align} & [F^{(13)}_{123}(\Xi_1 \times \Xi_3^c )](\omega) = [F_{123}(\Xi_1 \times \Xi_2 \times \Xi_3^c )](\omega) + [F^{(13)}_{123}(\Xi_1 \times \Xi_2^c \times \Xi_3^c )](\omega) =0 \end{align} したがって、(8.12)を得る.

(ii)と(iii)の証明は,　8.0節の文献[1,2]を見よ。



例 8.13 [例 8.5(トマト)からの続き]

$\Omega$， $C(\Omega{})$， ${\mathsf O}_{{1}}$ ${{=}}$ ${\mathsf O}_{{{}_{SW}}}$ ${{=}}$ $(X_{{}_{SW}} , $ $ 2^{ X_{{}_{SW}} } ,$ $ F_{{}_{SW}}{})$ と ${\mathsf O}_{{3}}$ ${{=}}$ ${\mathsf O}_{{}_{RD}}$ ${{=}}$ $(X_{{}_{RD}} ,$ $ 2^{ X_{{}_{RD}} } ,$ $ F_{{}_{RD}}{})$ は 例8.5と同じとする． $X_{{}_{RP}} = \{ y_{{}_{RP}} , n_{{}_{RP}} \} $ として， 観測量 ${\mathsf O}_{{2}}$ ${{=}}$ ${\mathsf O}_{{{}_{RP}}}$ ${{=}}$ $(X_{{}_{RP}} , 2^{ X_{{}_{RP}} } , F_{{}_{RP}}{})$ を新たに考える． ここに "$y_{{}_{RP}}$" と "$n_{{}_{RP}}$" はそれぞれ 「熟している」 と 「熟していない」$\!$ を意味する． \begin{align*} \mbox{Rep}[{}{\mathsf O}_1{}] & = \big[ [{}F_{{}_{SW}} (\{ y_{{{}_{SW}}} \}{}) {}] ({\omega_k}), [{}F_{{}_{SW}} (\{ n_{{{}_{SW}}} \}{}) {}] ({\omega_k}) \big] \\ \mbox{Rep}[{}{\mathsf O}_2{}] & = \big[ [{}F_{{}_{RP}} (\{ y_{{{}_{RP}}} \}{}) {}] ({\omega_k}), [{}F_{{}_{RP}} (\{ n_{{{}_{RP}}} \}{}) {}] ({\omega_k}) \big] \\ \mbox{Rep}[{}{\mathsf O}_3{}] & = \big[ [{}F_{{}_{RD}} (\{ y_{{{}_{RD}}} \}{}) {}] ({\omega_k}), [{}F_{{}_{RD}} (\{ n_{{{}_{RD}}} \}{}) {}] ({\omega_k}) \big] \end{align*} と置こう． そして， 次の擬積観測量を考える： \begin{align*} & {\mathsf O}_{12} = (X_{{}_{SW}} \times X_{{}_{RP}} , 2^{ X_{{}_{SW}} \times X_{{}_{RP}} }, F_{12} {{=}} F_{{}_{SW}} {{\mathop{\times}^{qp}}} F_{{}_{RP}}{}) \\ & {\mathsf O}_{23} = (X_{{}_{RP}} \times X_{{}_{RD}} , 2^{ X_{{}_{RP}} \times X_{{}_{RD}} }, F_{23} {{=}} F_{{}_{RP}} {{\mathop{\times}^{qp}}} F_{{}_{RD}}{}) \end{align*} いま， ${{\omega_k}}$ $\in \Omega$ として，

\begin{align} & [{\mathsf O}_{123}^{(1)};{\{y_{{}_{SW}} \}}] \underset{ {\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{123} , S_{ [{\omega_k}] }{}) }{ \Longrightarrow} [{\mathsf O}_{123}^{(2)};{\{y_{{}_{RP}} \}}] , \nonumber \\ & [{\mathsf O}_{123}^{(2)};{\{y_{{}_{RP}} \}}] \underset{ {\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{123} , S_{ [{\omega_k}] }{}) }{ \Longrightarrow} [{\mathsf O}_{123}^{(3)};{\{y_{{}_{RD}} \}}] \tag{8.14} \end{align} とする． このとき，定理8.12(i) により， 次を得る：

\begin{align*} & \; \;\;\; \mbox{Rep} [{}{\mathsf O}_{13}{}] = \left[\begin{array}{ll} [{}F_{13} ( \{ y_{{{}_{SW}}} \}\times \{ y_{{{}_{RD}}} \}){}] ({{\omega_k}} {}) & [{}F_{13} ( \{ y_{{{}_{SW}}} \}\times \{ n_{{{}_{RD}}} \}){}] ({{\omega_k}} {}) \\ {}[{}F_{13} ( \{ n_{{{}_{SW}}} \}\times \{ y_{{{}_{RD}}} \}){}] ({{\omega_k}} {}) & [{}F_{13} ( \{ n_{{{}_{SW}}} \}\times \{ n_{{{}_{RD}}} \}){}] ({{\omega_k}} {}) \\ \end{array}\right] \\ & = \left[\begin{array}{ll} [{}F_{{}_{SW}} (\{ y_{{}_{SW}} \}{}){}]({{\omega_k}} {}) & 0 \\ {}[{}F_{{}_{RD}} (\{ y_{{}_{RD}} \}{}){}]({{\omega_k}} {}) - [{}F_{{}_{SW}} (\{ y_{{}_{SW}} \}{}){}] ({{\omega_k}} {}) & 1 - [{}F_{{}_{RD}} (\{ y_{{}_{RD}} \}{}){}]({{\omega_k}} {}) \\ \end{array}\right] \end{align*}

したがって， 測定 ${\mathsf M}_{L^\infty (\Omega)} ( {\mathsf O}_{123} , S_{[{}{{{\omega_k}} }]}{}) $ により, トマト ${{\omega_k}} $ が「甘い」$\!\!\;$ と知ったとき， トマト ${{\omega_k}} $ が「赤い」 とわかる 確率は 次で与えられる：

\begin{align} \frac { [{}F_{13} ( \{ y_{{{}_{SW}}} \}\times \{ y_{{{}_{RD}}} \}){}] ({{\omega_k}} {}) } { [{}F_{13} ( \{ y_{{{}_{SW}}} \}\times \{ y_{{{}_{RD}}} \}){}] ({{\omega_k}} {}) + [{}F_{13} ( \{ y_{{{}_{SW}}} \}\times \{ n_{{{}_{RD}}} \}){}] ({{\omega_k}} {}) } = \frac{ [{}F_{{}_{RD}} (\{ y_{{}_{RD}} \}{}){}] ({{\omega_k}}{}) } { [{}F_{{}_{RD}} (\{ y_{{}_{RD}} \}{}){}] ({{\omega_k}}{}) } = 1 \tag{8.15} \end{align} もちろん， (8.14) は次を意味する： \begin{align*} \text{ "甘い" $\Longrightarrow$ "熟している" } \qquad \text{かつ} \qquad \text{ "熟している" $\Longrightarrow$ "赤い" } \end{align*} したがって，(8.12) より， 次の結論 ─ 当たり前の三段論法 ─ を得る： \begin{align*} \text{ "甘い" $\Longrightarrow$ "赤い" } \end{align*}

しかしながら, これはマーケットではあまり役に立たない． マーケットで役に立つのは \begin{align*} \text{ "赤い" $\Longrightarrow$ "甘い" } \end{align*} のような 結論である． 次の例で，これについて考える．



例 8.14 [例8.13から続く] (8.14) の代わりに, 次を仮定する： \begin{align} & [{\mathsf O}_{123}^{(1)};{\{y_{{}_{RD}} \}}] \underset{ {\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{123} , S_{ [{\omega_k}] }{}) }{ \Longleftarrow} [{\mathsf O}_{123}^{(2)};{\{y_{{}_{RP}} \}}] , \nonumber \\ & [{\mathsf O}_{123}^{(2)};{\{y_{{}_{RP}} \}}] \underset{ {\mathsf M}_{L^\infty (\Omega)} ({\mathsf O}_{123} , S_{ [{\omega_k}] }{}) }{ \Longrightarrow} [{\mathsf O}_{123}^{(3)};{\{y_{{}_{SW}} \}}] \tag{8.16} \end{align} ここで， トマト ${{\omega_k}} $ が「赤い」$\!\!\;$ と知ったとき， そのトマト ${{\omega_k}} $ が「甘い」 とわかる 確率は 次で与えられる： \begin{align*} & P = \frac{\text{{「"赤"かつ"甘い"」確率}}}{{\text{「赤い」確率}}}\\ & = \frac { [{}F_{13} ( \{ y_{{{}_{SW}}} \}\times \{ y_{{{}_{RD}}} \}){}] ({{\omega_k}} {}) } { [{}F_{13} ( \{ y_{{{}_{SW}}} \}\times \{ y_{{{}_{RD}}} \}){}] ({{\omega_k}} {}) + [{}F_{13} ( \{ n_{{{}_{SW}}} \}\times \{ y_{{{}_{RD}}} \}){}] ({{\omega_k}} {}) } \end{align*} これは，(8.3)から， 次のように評価できる： \begin{align} & {\small \text { $ \max \left\{ \frac{ [{}F_{{}_{RP}} (\{ y_{{}_{RP}} \}{})] ({{\omega_k}}{})} { [{}F_{{}_{RD}} (\{ y_{{}_{RD}} \}{})] ({{\omega_k}}{})} , \frac{ [{}F_{{}_{SW}} (\{ y_{{}_{SW}} \}{})] + [{}F_{{}_{RD}} (\{ y_{{}_{RD}} \}{})] -1 } { [{}F_{{}_{RD}} (\{ y_{{}_{RD}} \}{})] ({{\omega_k}}{})} \right\} {{\; \leqq \;}} P {{\; \leqq \;}} \min \left\{ \frac{ [{}F_{{}_{SW}} (\{ y_{{}_{SW}} \}{})] ({{\omega_k}}{}) } {[{}F_{{}_{RD}} (\{ y_{{}_{RD}} \}{})] ({{\omega_k}}{})} , \; 1 \right\} $ } } \\ & \tag{8.17} \end{align}

(8.16) は次と同値である： \begin{align*} \text{"熟している" $\Longrightarrow$ "甘い" } \qquad \text{かつ} \qquad \text{ "熟している" $\Longrightarrow$ "赤い" } \end{align*} これでは， 「甘い」と「赤い」の関係は何も 言えないと思うかもしれないが，上のように， \begin{align*} P = \frac{\text{{「"赤"かつ"甘い"」確率}}}{{\text{「赤い」確率}}} \end{align*} なので， (8.17)の評価は次に似ている： \begin{align*} \text{ "赤い" $\Longrightarrow$ "甘い" } \end{align*} したがって， 評価(8.17)はマーケットで役に立つかもしれない．
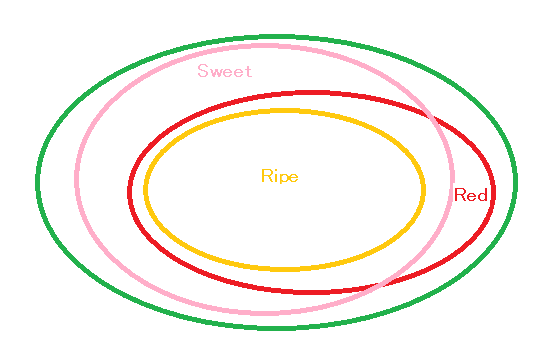
奇妙な結論と思うかもしれない。 しかし、下図を見れば、

$$ \frac{| \mbox{"Sweet"} \land \mbox{"Red"} |}{|\mbox{"Red"}|} \doteqdot 1 $$ なのだから、納得してもらえるだろう。

補足 (i): 上の例8.14は、著者の発見ではないかもしれない。　というよりは、　だれもが使っている「論理」かもしれない。 たとえば、 $$ いい女性\Longrightarrow美人、\qquad いい女性\Longrightarrow心がきれい、 $$ と信じていたとしよう。 そうすると、自然に、 $$ 美人\Longrightarrow心がきれい $$ と思い込んでしまうとしたら、これはよくある話だからである。 これが論理の飛躍とは、 一概に言えないことは、 例8.14で見たとおりである。


(ii): もちろん、最重要は、定理8.12(i)の「三段論法」である。 「三段論法の証明者」、　 すなわち、 「『ソクラテスは人間で、人間は死ぬ。よって、ソクラテスは死ぬ』の証明者」 という栄誉に著者が浴することがあるとしたら、 [定理8.12のProof (i)] が正しくてもだめで、右図が一般に承認されたときである。