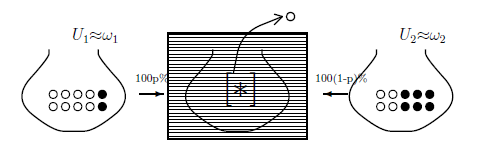
9.2:混合測定の簡単な例
どちらの壷($U_1$ または $U_2$)がカーテンの後ろに
置かれているのかあなたは知らない.
\\
カーテンの後ろの壷から球を一つ取り出したら,白球だった.
\\
このとき,壷は$U_1$または$U_2$のどちらか?$\;\;$これを推定せよ.
解答:
状態空間$\Omega=\{\omega_1, \omega_2\}$は離散距離を持ち,
測度$\nu$は次を満たすとする:
\begin{align}
\nu(\{ \omega_1 \})=1,
\qquad
\nu(\{ \omega_2 \})=1
\tag{9.3}
\end{align}
さて,古典系の基本構造
\begin{align*}
[C_0(\Omega) \subseteq L^\infty (\Omega, \nu ) \subseteq B(L^2 (\Omega, \nu ))]
\end{align*}
内の(純粋)測定
${\mathsf M}_{{L^\infty (\Omega) }} ({\mathsf O} {{=}}$
$
( \{ 白,$
$ 黒 \},$
$ 2^{\{ 白, 黒 \} } ,$
$ F{})
,
S_{ [{}{\ast}]}{})$
を考える.ここで,
$L^\infty (\Omega{})$内の観測量
${\mathsf O}_{白黒} = ( \{ 白, 黒 \}, 2^{\{ 白, 黒 \} } , F_{白黒}{})$
を次のように定義する:
\begin{align}
& [F_{白黒}(\{ 白 \}{})](\omega_1{})= 0.8, & \quad & [
F_{白黒}(\{ 黒 \}{})](\omega_1{})= 0.2
\nonumber
\\
& [F_{白黒}(\{ 白 \}{})](\omega_2{})= 0.4, & \quad & [F_{白黒}(\{ 黒 \}{})]
(\omega_2{})= 0.6
\tag{9.4}
\end{align}
そこで,
\begin{align*}
&
\max \{[F_{白黒}(\{白\})](\omega_1),
[F_{白黒}(\{白\})](\omega_2)
\}
\\
=
&
\max \{0.8, 0.4\}
=
0.8
=
F_{白黒}(\{白\})](\omega_1)
\end{align*}
であるから,定理5.6(フィッシャーの最尤法)により,
状態$\omega_1$が推定できて,
したがって,
カーテンの後ろの壷は$U_1$
であることが推定できる.
混合型言語ルール1
を丸暗記したら,練習・演習を繰り返そう
混合測定とフィッシャーの最尤法とを比較しながら,混合測定を理解したい.
したがって,
壷問題を通して,フィッシャーの最尤法の復習もしておこう.
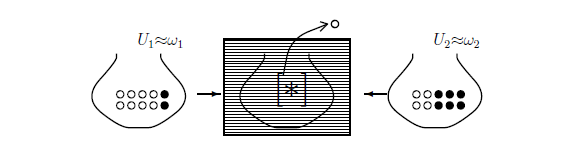
- Figure 9.2[ 混合測定 (壺問題)
| $(\sharp):$ | 公正とは限らないコイン投げ ($T_{p,1-p}$) $( 0 {{\; \leqq \;}}p {{\; \leqq \;}}1 )$を考える. すなわち, \begin{align*} コイン投げ(T_{p,1-p})によって, \begin{cases} 表が出る可能性は, \text{ $100p \% $} \\ 裏が出る可能性は, \text{ $100(1-p) \% $} \end{cases} \end{align*} とする. そして, 表が出たならば壷$U_1({\approx} \omega_1)$を, 裏が出たならば壷$U_2({\approx} \omega_2)$を, カーテンの後ろに置く. もちろん, それがどちらなのか($U_1$または$U_2$)はあなたは知らない. カーテンの後ろの壷の状態を$[*{}](\in \{\omega_1, \omega_2\})$ と記す |
| $(a):$ | カーテンの後ろの壷から球を一つ取り出したとき,それが白球である確率を求めよ. |
| $(b):$ | もし白球を取り出したとしたら, カーテンの後ろの壷が$U_1$である確率を求めよ. |
「解答」の前に,次を注意しておく.
| $\bullet$ | コイン投げを持ち出した理由は,「主観確率」を封印するためである. |
解答: 中高生でも簡単に正解できる問題であるが,以下に,「混合測定理論による解答」を示す. 状態空間$\Omega=\{\omega_1, \omega_2\}$は離散距離を持ち, 測度$\nu$は次を満たすとする:
\begin{align} \nu(\{ \omega_1 \})=1, \qquad \nu(\{ \omega_2 \})=1 \tag{9.5} \end{align} さて,古典系の基本構造 \begin{align} [C_0(\Omega) \subseteq L^\infty (\Omega, \nu ) \subseteq B(L^2 (\Omega, \nu ))] \tag{9.6} \end{align}内の(混合)測定 ${\mathsf M}_{{L^\infty (\Omega) }} ({\mathsf O} {{=}}$ $ ( \{ 白,$ $ 黒 \},$ $ 2^{\{ 白, 黒 \} } ,$ $ F{}) , S_{ [{}{\ast}]}{(w)})$ を考える.ここで, $L^\infty (\Omega{})$内の観測量 ${\mathsf O}_{白黒} = ( \{ 白, 黒 \}, 2^{\{ 白, 黒 \} } , F_{白黒}{})$ を次のように定義する:
\begin{align} & [F_{白黒}(\{ 白 \}{})](\omega_1{})= 0.8, & \quad & [ F_{白黒}(\{ 黒 \}{})](\omega_1{})= 0.2 \nonumber \\ & [F_{白黒}(\{ 白 \}{})](\omega_2{})= 0.4, & \quad & [F_{白黒}(\{ 黒 \}{})] (\omega_2{})= 0.6 \tag{9.7} \end{align} また,$w_0 \in L^1_{+1}(\Omega , \nu )$は次のように定める. \begin{align} w_0(\omega_1 ) = p, \qquad w_0(\omega_2)=1-p \tag{9.8} \end{align}(a): したがって, 混合言語ルール1に従って, (混合)測定 ${\mathsf M}_{{L^\infty (\Omega) }} ({\mathsf O} {{=}}$ $ ( \{ 白,$ $ 黒 \},$ $ 2^{\{ 白, 黒 \} } ,$ $ F{}) , S_{ [{}{\ast}]}{(w)})$によって,測定値 $x$ $(\in \{ 白 , 黒 \}{})$ が得られる確率は
\begin{align} P(\{ x \}{}) &= {}_{L^1(\Omega )} \big( w_0, F(\{x \}) \big)_{L^\infty(\Omega)} = \int_\Omega [F(\{ x \}{})]( \omega) \cdot w_0 (\omega) \nu(d \omega{}) \nonumber \\ & = p [F(\{ x \}{})](\omega_1) + (1-p) [F(\{ x \}{})](\omega_2) \nonumber \\ &= \begin{cases} 0.8 p + 0.4 (1-p{}) \quad & (x=白{}\; \text{のとき}) \\ 0.2 p + 0.6 (1-p{}) \quad & (x=黒{}\; \text{のとき}) \end{cases} \tag{9.9} \end{align} である.(b):解答9.13で答える.
| $\fbox{注釈9.1}$ |
次の疑問は自然である。
|
例 9.6[スピンの混合測定${\mathsf M}_{B({\mathbb C}^2)} ({\mathsf O}=(X= \{ \uparrow, \downarrow \} ,{2}^X, F^z ) , S_{[\ast]} (w) )$]
電子$P_1$のスピン状態は$\rho_1=|a \rangle \langle a|$ $\in$ ${\frak S}^p(B({\mathbb C}^2))$とする. ここで,
\begin{align*} a= \left[\begin{array}{ll} \alpha_1 \\ \alpha_2 \end{array}\right] \in {\mathbb C}^2 \quad (\mbox{ここに, }\|a \|= (|\alpha_1|^2+ |\alpha_2|^2)^{1/2}=1) \end{align*}とする. また, 電子$P_2$のスピン状態$\rho_2=|b \rangle \langle b|$ $\in$ ${\frak S}^p(B({\mathbb C}^2))$は,
\begin{align*} b= \left[\begin{array}{ll} \beta_1 \\ \beta_2 \end{array}\right] \in {\mathbb C}^2 \quad (\mbox{ここに, }\| b \|= (|\beta_1|^2+ |\beta_2|^2)^{1/2}=1) \end{align*} と表現する.ここで, 「電子$P$」が $ \left\{\begin{array}{ll} 電子P_1 \\ 電子P_2 \end{array}\right\} $ である「確率」は, $ \left\{\begin{array}{ll} p \\ 1-p \end{array}\right\} $ であるとしよう. したがって,「電子$P$」の状態は,混合状態$w$ $( \in$ ${\frak S}^p(B({\mathbb C}^2)))$は,
\begin{align*} w=p \rho_1 + (1-p) \rho_2 \end{align*} と表現できる.「電子$P$」の$z$-軸方向のスピン観測量の混合測定 ${\mathsf M_{B({\mathbb C}^2)}}({\mathsf O}_z =(X,2^X, F^z ), S_{[\ast]}(w))$を考える. ここに, ${\mathsf O}_z =(X,2^X, F^z )$ は次のように定まる:
\begin{align*} F^z( \{ \uparrow \}) = \left[\begin{array}{ll} 1 & 0 \\ 0 & 0 \end{array}\right] , \quad F^z( \{ \downarrow \}) = \left[\begin{array}{ll} 0 & 0 \\ 0 & 1 \end{array}\right] \end{align*} \rm| $(a):$ | 混合測定 ${\mathsf M_{B({\mathbb C}^2)}}({\mathsf O}_z =(X,2^X, F^z ), S_{[\ast]}(w))$ によって, 測定値 $ \left\{\begin{array}{ll} \uparrow \\ \downarrow \end{array}\right\} $ を得る確率は \begin{align*} \left\{\begin{array}{ll} {}_{{\mathcal Tr}({\mathbb C}^2)} \Big(w, F^z( \{ \uparrow \}) \Big) {}_{B({\mathbb C}^2)} = p|\alpha_1|^2 +(1-p) |\beta_1|^2 \\ \\ {}_{{\mathcal Tr}({\mathbb C}^2)} \Big(w, F^z( \{ \downarrow \}) \Big) {}_{B({\mathbb C}^2)} = p |\alpha_2|^2 + (1-p)|\beta_2|^2 \end{array}\right\} \end{align*} |
注意9.7
上で見たように,
| $(a):$ | 純粋測定理論が基本で, それに混合状態の概念が付け加わって混合測定理論が構築される. すなわち, \begin{align} \underset{\mbox{ ${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O} , {\overline S}_{[\ast ]}{(w)}) $}}{\mbox{$\fbox{ 混合測定理論 }$}} := { { \underset{\mbox{ ${\mathsf M}_{L^\infty (\Omega)} ({\mathsf O} , S_{[\ast ]}) $}}{\mbox{ $\fbox{ 純粋測定理論 }$}}} } + { { \underset{\mbox{ $w$}} {\mbox{$\fbox{ 混合状態}$}} } } \end{align} |
- 純粋測定無くして,混合測定無し