まず,
サンクトペテルブルクの二つの封筒問題
を復習しておく.
として,
$L^\infty (\Omega )$内の精密観測量
${\mathsf O}=(X, {\mathcal F}, F )$
を次のように定める.
混合状態$w_0$
(i.e., $\Omega$上の確率密度関数)
を以下のように定義する.
ここで,混合測定
${\mathsf M}_{L^\infty (\Omega )} ({\mathsf O}=(X, {\mathcal F}, F ),
{\overline S}_{[\ast]}(w_0) )$を得る.
言語ルール$^{{ (m)}}$ 1(C$_1$)($\S$9.1)
に従えば、
と計算できる.
問題9.8では,封筒Aの中身は,
$x=2^m$であった.
あなたは,未だ封筒Bの中を見ていないのだから,
期待値$E=\infty$に頼るのは理屈がある.
そうならば,
$E=\infty > 2^m$
なのだから,
あなたは,
「封筒Bに変更しよう」と思うだろう.
もちろん、
この判断が悪いわけがない。
本節は,次からの抜粋:
$(\sharp):$
S. Ishikawa;
two envelopes paradox in non-Bayesian and Bayesian statistics
$\quad$
(
arXiv:1408.4916v4 [stat.OT] 2014
)
$(a):$
公平なコインを表が出るまで投げる.
$n$回目に初めて表が出たとする.
このとき,封筒Aの中に$2^n$円を入れた.
あなたはこのことを知っているが,回数$n$を知っているわけではない.
封筒Bの中にも同じ手続きでお金を入れた.
$(b):$
あなたは, 公正なコイン投げによって、封筒Aを選んだとしよう.
封筒Aを開けてみたら,$x=2^m$円入っていた.
ここで,あなたには,封筒Bに変更するという選択肢がある.
さて,封筒Aのままにして,$x=2^m$円を獲得するか?
または,封筒Bに変更して,新たなチャンスに賭けるか?
さて,あなたはどうする.

[(P2):どこがパラドックスなのか ?]
封筒Aを開けてみたら,$x=2^m$円入っていた.
封筒Bはまだ開いていないが,
期待値$E(y)$は次のように計算できる
\begin{align*}
E(y)= 2 \times \frac{1}{2} + 2^2 \times \frac{1}{2^2}+
2^3 \times \frac{1}{2^3}+\cdots = \infty
\end{align*}
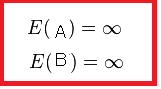 そうだとすると,封筒Bに変更して,新たなチャンスに賭けたくなる.
すなわち、
そうだとすると,封筒Bに変更して,新たなチャンスに賭けたくなる.
すなわち、
である。
しかし,これはおかしい. なぜならば,
封筒Aと封筒Bの役割
は同じはずだからである.
このパラドクスが,有名な「サンクトペテルブルグの二つの封筒問題」である.
(P2): サンクトペテルブルグの二つの封筒問題:
古典混合測定
状態空間$\Omega$を
\begin{align*}
\Omega=\{\omega =2^m \; |\; m =1,2, \cdots \}
\end{align*}
とする.離散距離空間を想定して, $\nu$を$\Omega$上の個数測度とする.
\begin{align*}
L^\infty (\Omega)
=
\{
f \;|\;
\mbox{$f$は$\Omega$上の複素数値有界関数}
\}
\end{align*}
$(a):$
${\mathsf M}_{L^\infty (\Omega )} ({\mathsf O}=(X, {\mathcal F}, F ),
{\overline S}_{[\ast]}(w_0))$によって得られる
測定値$x (\in X)$
が
$
2^m
$
に等しくなる
確率は
$
2^{-m}
$
である
と言える.
したがって,測定値の期待値$E$は
\begin{align*}
E= \sum_{k=1}^\infty 2^k \cdot 2^{-k}= \infty
\end{align*}
注意9.9
上の議論から,
[(P2):どこがパラドックスなのか?]の中に書いた文言
「封筒A
と
封筒B
の役割は同じ」
は
疑わしい.
| $\bullet$ | あなたは,封筒Aの中身は$2^m$円(測定値)であることを知った. ということは, 確率密度関数$w_1$が $$ w_1(\omega) =\begin{cases} 1 \quad & \mbox{( $\omega = 2^m$)} \\ 0 & \mbox{($\omega \not= 2^m$)} \end{cases} $$ であることを知ることに等しい(cf. ベイズの定理(in $\S$9.4) ). |
したがって, 封筒$A$の確率密度関数$w_1$と封筒$B$の確率密度関数$w_0$を比べることになるが, 上の議論のように,$B$の期待値は$\infty$なのだから, この場合には,ことわざ "The Other Person's envelope is Always Greener" は正しい.
すなわち、- $A$と$B$は、「対称」というわけではない
とは言え、これは「後出しの理由づけ」かもしれない。 世界記述無しに、「対称性」を持ち出すのは違法(cf. $\S$5.6: 天動説 vs, 地動説) なのだから、「サンクトペテルブルグの二つの封筒問題」はベイズ統計下で議論すべきこと なのだと思う。
補足: 著者は、「二つの封筒問題」に関しては、何度も勘違いしている。 まだ、本当のことをわかっていなかもしれない。 上の議論通りだとすると、 この節は、ベイズ統計(次節)以降に書くべきであった。
| $\fbox{注釈9.2}$ |
期待値以外にも様々な基準が考えられる.
たとえば,
という基準で決めるとする. この場合は, 封筒Aの中身は$2^m$円(測定値)であることを知ったときに, $$ \begin{cases} m = 1 &\Longrightarrow \mbox{交換する} \\ m=2,3,... & \Longrightarrow \mbox{交換しない} \end{cases} $$ となる |
