交換写像$\overline{x}:
\{V_1, V_2 \} \to
\{V_1, V_2\}
$を
$\overline{x} =
\begin{cases}
V_2,\;\; (\mbox{ if } x=V_1),
\\
V_1 \;\; (\mbox{ if } x=V_2)
\end{cases}
$
で定める.
あなたは無作為に(公正なコイン投げによって)一方の封筒を
選んだとしよう.
そして,
$x_1$円を得たとする.
(すなわち,
封筒A[resp B]ならば,
$V_1$円[resp. $V_2$円]
得たことになる).
このとき,
主催者は,$\overline{x}_1$円得ることになる.
したがって,あなたは
「$\overline{x}_1=x_1/2$」
または
「$\overline{x}_1=2x_1$」と推定できる.
ここで,あなたには,あなたの$x_1$円と主催者の$\overline{x}_1$円と変更するという選択肢があるとしよう.$x_1=\alpha$としよう.
さて,このままにして,$\alpha$円を獲得するか?
または,変更して,$\alpha/2$円または$2\alpha$円を獲得するか?
さて,あなたはどうする.
[(P1):どこがパラドックスなのか ?].
あなたは次のように考えるかもしれない. 確率1/2で, もう一方の封筒$B$は,$\alpha/2$円か,または$2\alpha$円入っているに違いない. したがって,封筒$B$内のお金の期待値(それをE($\alpha$)と記す)は,
\begin{align}
E(\alpha)=(1/2)(\alpha/2) + (1/2)(2\alpha)
\tag{9.18}
\end{align}
で, すなわち,$E(\alpha)=1.25\alpha$となる.これは封筒$A$の$\alpha$円より大きい.
したがって,「封筒$A$を封筒$B$に変更しよう」とあなたは考えるだろう.
同一視
:
$\widehat{\Omega} \ni (\omega, 2\omega ) \longleftrightarrow \omega \in \Omega =\overline{\mathbb R}_+$の下に、
次を仮定する:
\begin{align*}
\rho_0(D) =\int_D w_0(\omega ) d \omega
\quad
(\forall D \in {\mathcal B}_{\Omega }={\mathcal B}_{\overline{\mathbb R}_+ })
\end{align*}
ここに
確率密度関数
$w_0: \Omega ( \approx \overline{\mathbb R}_+ ) \to
\overline{\mathbb R}_+ $
は連続とし、
混合状態$\rho_0 (\in {\mathcal M}^m(\Omega(=\overline{\mathbb R}_+ ) ) )$
は
確率密度関数$w_0 (= h)$を持つとする。
ここで,
混合型言語ルール${}^{\rm (m)}$1($\S$9.1)
によって,
次が言える.
したがって,
変更してもしなくても,利得は変わらない.
ゲームの主催者は,あなたに二つの封筒
(i.e.,
封筒Aと
封筒B)から一つの封筒を選ぶチャンスを提供した.
封筒Aと
封筒Bにそれぞれ
$V_1$円と$V_2$円が入っている.
あなたには,次が知らされている.
$(a):$
$\qquad
\frac{V_1}{V_2}=1/2$
または,
$\frac{V_1}{V_2}=2$

 なぜならば,
封筒A
と
封筒B
の役割は同じはずだからである.あなたがランダムに(i.e.,
確率1/2で)選んだのが,
封筒Bだとすると,こんどは封筒Aを選ぶのだろうか?
このパラドクスが,有名な「二つの封筒問題(i.e.,
"The Other Person's envelope is Always Greener"
)」である.
なぜならば,
封筒A
と
封筒B
の役割は同じはずだからである.あなたがランダムに(i.e.,
確率1/2で)選んだのが,
封筒Bだとすると,こんどは封筒Aを選ぶのだろうか?
このパラドクスが,有名な「二つの封筒問題(i.e.,
"The Other Person's envelope is Always Greener"
)」である.
9.5.1:(P1): 二つの封筒問題のベイズ統計による解答
状態空間$\Omega$
を次のように定める。
\begin{align*}
\Omega=\overline{\mathbb R}_+
(=\{ \omega \in {\mathbb R} \;|\; \omega \ge 0 \})
\end{align*}
もちろん、ルベーグ測度$\nu$
を仮定する。
次の古典基本構造から始めよう:
\begin{align*}
[
C_0(\Omega )
\subseteq L^\infty ( \Omega , \nu )
\subseteq
B(L^2 ( \Omega , \nu )
)
]
\end{align*}
また、
$\widehat{\Omega}=\{ (\omega, 2 \omega ) \;| \; \omega \in \overline{\mathbb R}_+
\}$
と置いて、
次の同一視を考える:
\begin{align}
\Omega \ni \omega \underset{\mbox{(identification)}}{\longleftrightarrow} (\omega, 2 \omega ) \in \widehat{\Omega}
\tag{9.19}
\end{align}
さらに,
写像
$V_1:\Omega (\equiv \overline{\mathbb R}_+) \to X(\equiv \overline{\mathbb R}_+)$
と
$V_2:\Omega (\equiv \overline{\mathbb R}_+) \to X(\equiv \overline{\mathbb R}_+)$
を次のように定める:
\begin{align*}
V_1(\omega ) =\omega , \quad V_2(\omega ) = 2 \omega
\qquad
(\forall \omega \in \Omega)
\end{align*}
また、$L^\infty (\Omega, \nu )$内の観測量
${\mathsf O}=(X(=\overline{\mathbb R}_+), {\mathcal F}(={\mathcal B}_{\overline{\mathbb R}_+}:\mbox{ the Borel field}), F )$
を次のように定める:
\begin{align*}
&
\qquad
[F(\Xi )](\omega )=
\begin{cases}
1
\qquad & (\mbox{ if } \omega \in \Xi, \;\; 2 \omega \in \Xi)
\\
1/2
\qquad & (\mbox{ if } \omega \in \Xi, \;\; 2 \omega \notin \Xi)
\\
1/2
\qquad & (\mbox{ if } \omega \notin \Xi, \;\; 2 \omega \in \Xi)
\\
0
\qquad & (\mbox{ if } \omega \notin \Xi, \;\; 2 \omega \notin \Xi)
\end{cases}
\qquad
(\forall \omega \in \Omega, \forall \Xi \in
{\mathcal F}
)
\end{align*}
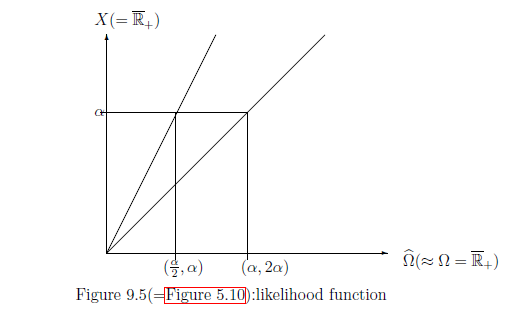
したがって,測定値の期待値は
\begin{align}
\int_{\overline{\mathbb R}_+} x P(d x )
=
\frac{1}{2}
\int_{0}^\infty
x
\cdot
\Big(
h(x/2 )/2
+
h(x )
\Big)
d x
=
\frac{3}{2}
\int_{\overline{\mathbb R}_+} x h(x ) d x
\tag{9.21}
\end{align}
となる.
また,
ベイズの定理から,
$(D_1):$
混合測定
${\mathsf M}_{L^\infty (\Omega, d \omega )} ({\mathsf O}=(X, {\mathcal F}, F ),
S_{[\ast]}(\rho_0))$
によって得られた測定値が
$\Xi (\in {\mathcal B}_X ={\mathcal B}_{\overline{\mathbb R}_+ })$
に属する
確率$P(\Xi)$
$(\Xi \in {\mathcal B}_X ={\mathcal B}_{\overline{\mathbb R}_+ })$
は次で与えられる.
\begin{align}
P (\Xi )
&
=
\int_\Omega [F(\Xi )](\omega ) \rho_0 (d \omega )
=
\int_\Omega [F(\Xi )](\omega ) h (\omega ) d \omega
\nonumber
\\
&
=
\int_{\Xi}
\frac{h(x/2 )}{4}
+
\frac{h(x )}{2}
\;\;
d x
\quad
(\forall \Xi \in {\mathcal B_{\overline{\mathbb R}_+ }})
\tag{9.20}
\end{align}
したがって,
$(D_2):$
混合測定
${\mathsf M}_{L^\infty (\Omega, d \omega )} ({\mathsf O}=(X, {\mathcal F}, F ),$
$
S_{[\ast]}(\rho_0))$によって,
測定値$\alpha (\in X(=\overline{\mathbb R}_+))$
を得たとき,
事後状態
$\rho_{\mbox{ post}}^\alpha
(\in {\mathcal M}^m (\Omega ))$
は次で与えられる.
\begin{align}
\rho_{\mbox{ post}}^\alpha
=
\frac{
\frac{h(\alpha/2)}{2}
}
{\frac{h(\alpha/2)}{2}
+
h(\alpha)
}
\delta_{(\frac{\alpha}{2}, \alpha)}
+
\frac{
h(\alpha)
}
{\frac{h(\alpha/2)}{2}
+
h(\alpha)
}
\delta_{({\alpha}{},2 \alpha)}
\tag{9.22}
\end{align}
$(D_3):$
もし
$[\ast]
=
$
$
\left\{\begin{array}{ll}
\delta_{(\frac{\alpha}{2}, \alpha)}
\\
\delta_{({\alpha}{}, 2 \alpha)}
\end{array}\right\}
$ならば,
あなたは変更は
$
\left\{\begin{array}{ll}
\alpha \longrightarrow \frac{\alpha}{2}
\\
\alpha \longrightarrow 2{\alpha}
\end{array}\right\}
$
であって,
変更の利得は
$
\left\{\begin{array}{ll}
\frac{\alpha}{2} - \alpha
(= - \frac{\alpha}{2} )
\\
2{\alpha} - \alpha
(= {\alpha})
\end{array}\right\}
$
となる.
したがって,
変更による利得の期待値は
次のように計算できる.
\begin{align}
&
\int_{\overline{\mathbb R}_+}
\Big(
(-\frac{\alpha}{2})
\frac{
\frac{h(\alpha/2)}{2}
}
{\frac{h(\alpha/2)}{2}
+
h(\alpha)
}
+
\alpha
\frac{
h(\alpha)
}
{\frac{h(\alpha/2)}{2}
+
h(\alpha)
}
\Big)
P(d \alpha )
\nonumber
\\
=
&
\int_{\overline{\mathbb R}_+}
(-\frac{\alpha}{2})\frac{h(\alpha/2 )}{4}
+
\alpha \cdot \frac{h(\alpha )}{2}
\;\;
d \alpha
=0
\tag{9.23}
\end{align}
$(E_1):$
開封: $(D_2)$で、測定値$\alpha$の値を知ってから判断する
とする。
$(E_2):$
未開封: $(D_2)$で、測定値$\alpha$の値を知らずに判断する
開封の場合は明らかと思って、未開封の場合だけを上では議論した(上の議論が未開封の場合と同じことの議論は
自明なので省略する)。
しかし、開封の場合も述べておいた方が理解を深めるかもしれないので、以下のように補足しておく。
式(9.22)より、もう一方の封筒の期待値は、
\begin{align}
\frac{
\frac{h(\alpha/2)}{2} \times \frac{\alpha}{2}
}
{\frac{h(\alpha/2)}{2}
+
h(\alpha)
}
+
\frac{
h(\alpha)
\times 2 \alpha
}
{\frac{h(\alpha/2)}{2}
+
h(\alpha)
}
\end{align}
であるから、これを測定値$\alpha$と比較すればよい。結果だけ書くと、
$4h(\alpha) \ge h(\alpha/2)$のとき交換、
$4h(\alpha) \le h(\alpha/2)$のとき非交換
となる。
9.5: 二つの封筒問題(ベイズ統計学)
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
問題9.14 [二つの封筒問題(問題5.16の再掲)]
サプリ
上だけでは、説明不十分かもしれないので、補足しておく。
分布$\rho_0$が既知か未知かであるが、未知ならば5.6節に帰すのだから、既知とする。
次は開封か未開封かの問題である。
ここで、
$\square \quad$
