9.7.1:等重率(=等確率の原理)─最も簡単で有名な未解決問題
モンティ・ホール問題
(問題9.15(フィッシャーの最尤法),問題9.16(ベイズの方法))
をもう一度考え直そう.
次が
モンティ・ホール問題
のベイズの方法による解答のもう一つの決定版と考える
(また、もう一つの決定版は問題19.5を見よ).
解答
問題9.15と問題9.16
(モンティ・ホール問題)
のように,
状態空間$\Omega = \{ \omega_1 , \omega_2 , \omega_3 \}$
と
観測量
${\mathsf O}=(X, {\cal F}, F)$
を定める.
写像
$\phi:\Omega \to \Omega $
を
\begin{align*}
\phi(\omega_1) =\omega_2,
\quad
\phi(\omega_2) =\omega_3,
\quad
\phi(\omega_3) =\omega_1
\quad
\end{align*}
で定めて,
因果作用素$\Phi:L^\infty(\Omega) \to L^\infty(\Omega)$
を
$[\Phi(f)](\omega)
=
f(\phi(\omega))$
$(\forall f \in L^\infty(\Omega), \;\forall \omega \in \Omega )$
で定める
(因果作用素については,次章以降で議論するので,ここでは深入りしない).
さて,
自動車が$k$番ドアの後ろに置いてあるとしよう$(k=1,2,3)$.
ここで,次が言える:
と考える.
したがって,
上の(a)は,
次と同一視できる.
ここで,
$\frac{1}{3}(\delta_{\omega_k}+\delta_{\phi(\omega_k)}
+\delta_{\phi^2 (\omega_k)})$
$=$
$\frac{1}{3}(\delta_{\omega_1}+\delta_{\omega_2}
+\delta_{\omega_3})$
$(\forall k=1,2,3)$
に注意せよ.
したがって,
この(c)は,
次を満たす混合状態$w_e (\in L^1_{+1}(\Omega ))$
に対する
混合測定
${\mathsf M}_{L^\infty(\Omega)} ({\mathsf O}, {\overline S}_{[{}\ast{}]}(w_e ))$
と等しい.すなわち,
以上の議論から,等重率(=等確率の原理)
は,次の定理9.18で示される.
定理 9.18 [等重率(=等確率の原理)]
状態空間$\Omega(\approx {\frak S}^p(C_0(\Omega)^*))$を有限集合とする.
すなわち,
$\Omega=\{\omega_1,\omega_2,\ldots,\omega_n\}$
として,測度$\nu$を
$\nu(\{\omega_k \})=1/n \;\;(\forall \omega_k \in \Omega )$とする.
${\mathsf O}=(X, {\cal F}, F)$
を
$L^\infty(\Omega)$内の観測量とする.
測定者が状態についての情報を持っていないときに,
通常は純粋測定$
{\mathsf M}_{L^\infty(\Omega )}({\mathsf O} ,
S_{[
\ast]}
)
$
を考える.
しかし,
別の方法として,
$w_e (\omega)=
\frac{1}{n}
\;\;
(\forall \omega \in \Omega )$
として,
混合測定
$
{\mathsf M}_{L^\infty(\Omega )}({\mathsf O} ,
{\overline S}_{[
\ast]}(w_e)
)
$
を考えることは,
(
問題9.17
の$({{\sharp}})$の意味では)
一理ある.
証明
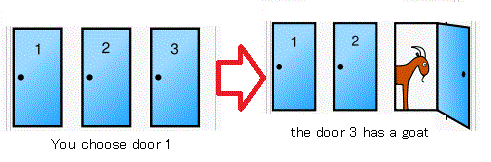
問題9.17 [モンティホール問題(等重率(=等確率の原理))]
$\quad$
あなたはゲームショーに出演している.
3つのドア
(すなわち,「1番」,「2番」,「3番」)
のうちの
1つのドアの後ろには{自動車}, 他の2つのドアの後ろには
羊(はずれ)が隠されている.
司会者は,
どのドアの後ろに自動車が隠されているかを
知っている.
しかし,あなたはそれを知らない.
司会者は問う:
「どのドアの後ろが自動車だと思いますか?」
ここで,
あなたは次のようにしてドアを選ぶとする.
$(\sharp):$
あなたはサイコロを投げて,
出た目が1,2
ならば
1番ドア,
3,4
ならば
2番ドア,
5,6
ならば
3番ドア
を選ぶとする.
このようにして,
たとえば,
1番のドアを選んだとする.このとき,
司会者が
「実は,3番ドアの後ろは羊です」
と言う.
更に,司会者は問う.
「あなたは1番のドアを選んでしまいましたが,
今からでも変更可能ですよ.
2番のドア
に変更しますか?
」と.
さて,あなたはどうするか?
である.
問題9.16の繰り返しになるが,
たとえば,
サイコロの目が「3」だったとしたら,
あなたは測定
${\mathsf M}_{L^\infty(\Omega)} (\Phi {\mathsf O}, S_{[{}\ast{}]})$
─
「3番ドアの後ろに自動車が隠れている」
と言って,
司会者の反応を見る測定
─
を行うことになる.
ここで,
$(a):$
$
\text{サイコロの出た目が}
\left[\begin{array}{ll}
1,2
\\
3,4
\\
5,6
\end{array}\right]
\text{ならば,測定}
\left[\begin{array}{ll}
{\mathsf M}_{L^\infty(\Omega)} ({\mathsf O}, S_{[{}\omega_k{}]})
\\
{\mathsf M}_{L^\infty(\Omega)} (\Phi{\mathsf O}, S_{[{}\omega_k{}]})
\\
{\mathsf M}_{L^\infty(\Omega)} (\Phi^2{\mathsf O}, S_{[{}\omega_k{}]})
\end{array}\right]
を行う
$
$(b1):$
測定${\mathsf M}_{L^\infty(\Omega)} (\Phi{\mathsf O}, S_{[{}\omega_k{}]})$の測定値が$\Xi (\in {\mathcal F} )$に属する確率は,$[\Phi (F(\Xi)](\omega_k)$である
この意味で,次の同一視:
\begin{align*}
{\mathsf M}_{L^\infty(\Omega)} (\Phi{\mathsf O}, S_{[{}\omega_k{}]})
\underset{同一視}{\longleftrightarrow}
{\mathsf M}_{L^\infty(\Omega)} ({\mathsf O}, S_{[{}\phi(\omega_k){}]})
\end{align*}
を考える.
同様に,
\begin{align*}
{\mathsf M}_{L^\infty(\Omega)} (\Phi^2{\mathsf O}, S_{[{}\omega_k{}]})
\underset{同一視}{\longleftrightarrow}
{\mathsf M}_{L^\infty(\Omega)} ({\mathsf O}, S_{[{}\phi^2 (\omega_k){}]})
\end{align*}
$(b2):$
測定${\mathsf M}_{L^\infty(\Omega)} ({\mathsf O}, S_{[{}\phi(\omega_k){}]})$の測定値が$\Xi (\in {\mathcal F} )$に属する確率は,$[ (F(\Xi)](\phi(\omega_k))$
(=
$[\Phi (F(\Xi)](\omega_k)$
)である
$(c):$
$
\text{サイコロの出た目が}
\left[\begin{array}{ll}
1,2
\\
3,4
\\
5,6
\end{array}\right]
\text{ならば,測定}
\left[\begin{array}{ll}
{\mathsf M}_{L^\infty(\Omega)} ({\mathsf O}, S_{[{}\omega_k{}]})
\\
{\mathsf M}_{L^\infty(\Omega)} ({\mathsf O}, S_{[{}\phi (\omega_k){}]})
\\
{\mathsf M}_{L^\infty(\Omega)} ({\mathsf O}, S_{[{}\phi^2(\omega_k){}]})
\end{array}\right]
を行う
$
$\fbox{注釈9.4}$
上の議論は,簡単な理屈で,
「あなた(=測定者)は
どのドアか知らないのだから,フェアなサイコロを投げて決めた」
と考えただけである.
しかし,この仕組みを測定理論で記述することは,
上述のように簡単とは言えない.
たとえば,問題9.17
の
$(\sharp)$で,
測定者がアンフェアなサイコロ投げをしたとしたら,
計算できなくなって何も言えなくなってしまう.
このことは,
問題9.16の
$(\sharp)$では,ゲームの主催者がアンフェアなサイコロ投げをしたとしても
計算可能であることとの比較の中で,
注意すべきである.

証明は
問題9.17
の解答と同様な議論から容易にわかる.
また、次を見よ。
$(\sharp):$
S. Ishikawa, "A 測定Theoretical Foundation of Statistics,"
Applied Mathematics, Vol. 3, No. 3, 2012, pp. 283-292
$\fbox{注釈9.5}$
この講義では、三つの等確率の原理を議論する:
$(\sharp_1):$
注意5.19の等確率の原理($\S$5.6)
$(\sharp_2):$
定理9.18の等確率の原理($\S$9.7)
$(\sharp_3):$
公準18.4の等確率の原理($\S$18.2)
9.7:モンテイ・ホール問題(等確率の原理)
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
$\square \quad$
$\square \quad$
