本節は,次からの抜粋:
$(\sharp):$
S. Ishikawa;
Final Solutions of Monty Hall problem and Three Prisoners Problem
arXiv:1408.0963v1 [stat.OT] 2014
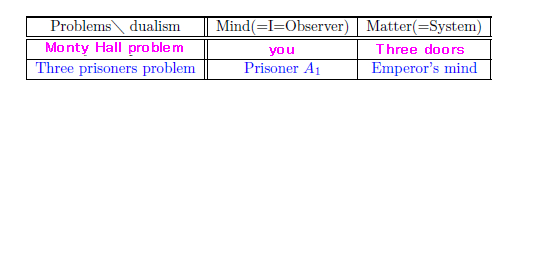
- モンティホール問題 と三囚人の問題は「同型問題」である
とは、よく言われていることであるが,この「同型」の意味を本当にわかっている研究者を知らない. したがって, この節では,同時にこの二つを
| $\bullet$ | $ \qquad \begin{cases} \textcolor{magenta}{\mbox{モンティホール問題}} \\ \textcolor{blue}{\mbox{三囚人の問題}} \end{cases} $ |
| $\bullet$ | 明確な 二元論の構造 を持った理論(量子 言語)の中で, モンティホール問題 と 三囚人の問題 を同時に議論しなければ, 「同型」は見えてこない. |
9.9.1: フィッシャー統計学: モンティ・ホール問題 [resp. 三囚人の問題 ]
問題9.21(=問題9.15=問題5.14[モンティホール問題])
| $\quad$ |
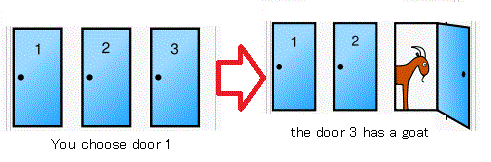
あなたはゲームショウに参加している.三つのドア
(i.e., ドア$A_1$, ドア$A_2$, ドア$A_3$)があって,
一つのドアの後ろには『自動車』が,
また他の二つのドアの後ろには『羊』が隠されている. 司会者はドアの後ろが見えるが,あなたには見えない.
司会者が,「どのドアの後ろに,『自動車』が隠されていると思いますか?」
とあなたに問う.ゲームなので,あなたは
ドア$A_1$と答えたとしよう.
そこで,司会者はドア$A_3$の後ろは,『羊』ですよ」とあなたに教えてくれた.
さらに,司会者は
「あなたは,ドア$A_1$と言ってしまいましたが,いまからでも,ドア$A_2$に変更できますよ」と言った.さて,ここで,
|
問題9.22[三囚人の問題]
| $\quad$ |
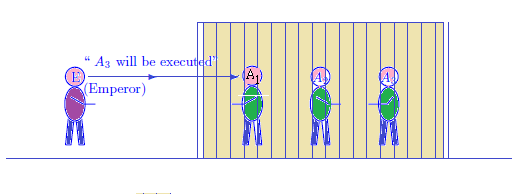
三人の死刑囚$A_1$, $A_2$と$A_3$が牢屋に入っている.
皇帝によって,三人の内の一人は恩赦で,罪を許されたが,
恩赦された者が誰だかは,皇帝は知っているが,三人には知らされていない.
ここで,囚人$A_1$が皇帝に次のように言った.
「 私以外の二人の内で,すくなくとも一人は,死刑のはず.
その一人を私だけに教えてくれませんか?」
皇帝はすこし考えたが,
「囚人$A_1$には,関係ないことなので,いいか」と思って,
「$A_3$さんは死刑だよ」
と答えた.
そこで, 囚人$A_1$は次のように考えた.
|
9.9.2:解答(フィッシャー統計学): モンティ・ホール問題 [resp. 三囚人の問題 ]
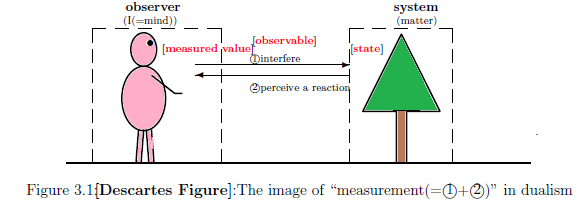
デカルト図式を確認しよう。
- デカルト図式9.7: "測定"(=二元論)のイメージ
二元論(物心二元論)の対立関係
\begin{align} \mbox{ "測定者$\longleftrightarrow$物" } \end{align} は、以下のようになる。離散距離空間$\Omega$を $\Omega = \{ \omega_{1} , \omega_{2} , \omega_{3} \}$ とする. ここで,各状態 $\delta_{\omega_{{m}}} (\in {\frak S}^p (C(\Omega)^* ))$ は,次を意味するとする.
\begin{align} & \textcolor{magenta}{\mbox{ $ \delta_{\omega_{{m}}} \Leftrightarrow $ }} \textcolor{magenta}{ \mbox{ドア$A_m$の後ろに『自動車』がある状態} } \\ %[\mbox{resp.} \;\;\; & \textcolor{blue}{\mbox{ $ \delta_{\omega_{{m}}} \Leftrightarrow $ }} \textcolor{blue}{ \mbox{囚人$A_m$が恩赦を受ける状態} } %] \\ & \qquad \qquad (m=1,2,3 ) \tag{9.28} \end{align}$C(\Omega)$内の観測量 ${\mathsf O}_1$ $\equiv$ $({}\{ 1, 2,3 \}, 2^{\{1, 2 ,3\}}, F_1)$を以下のように定める.
\begin{align} & [F_1({}\{ 1 \}{})](\omega_1{})= 0.0,\qquad [F_1({}\{ 2 \}{})](\omega_1{})= 0.5, \qquad [F_1({}\{ 3 \}{})](\omega_1{})= 0.5, \nonumber \\ & [F_1({}\{ 1 \}{})](\omega_2{})= 0.0, \qquad [F_1({}\{ 2 \}{})](\omega_2{})= 0.0, \qquad [F_1({}\{ 3 \}{})](\omega_2{})= 1.0, \nonumber \\ & [F_1({}\{ 1 \}{})](\omega_3{})= 0.0,\qquad [F_1({}\{ 2 \}{})](\omega_3{})= 1.0, \qquad [F_1({}\{ 3 \}{})](\omega_3{})= 0.0, \tag{9.29} \end{align}よって,
「測定
${\mathsf M}_{C({}\Omega{})} ({}{\mathsf O}_1, S_{[{}\ast{}]})$を行う」
とは,
である.
したがって,次の対応を考える.
| $\bullet$ | $\quad$ $ \begin{cases} \textcolor{magenta}{ \mbox{ あなたが「ドア$A_1$」と言う } } \\ \textcolor{blue}{ \mbox{ 「囚人$A_1$」が皇帝に「他の二人のどっちが死刑か?」と問う } } \end{cases} $ |
| $(a):$ |
測定
${\mathsf M}_{C({}\Omega{})} ({}{\mathsf O}_1, S_{[{}\ast{}]})$により,
測定値「1」を得る
$ \Leftrightarrow \begin{cases} \textcolor{magenta}{ \mbox{司会者が「ドア$A_1$の後ろに 『羊』がいる」と言う } } \\ \textcolor{blue}{ \mbox{皇帝が「囚人$A_1$ は死刑になる」と言う } } \end{cases} $ |
| $(b):$ |
測定
${\mathsf M}_{C({}\Omega{})} ({}{\mathsf O}_1, S_{[{}\ast{}]})$により,
測定値「2」を得る
$ \Leftrightarrow \begin{cases} \textcolor{magenta}{ \mbox{司会者が「ドア$A_2$の後ろに 『羊』がいる」と言う } } \\ \textcolor{blue}{ \mbox{皇帝が「囚人$A_2$ は死刑になる」と言う } } \end{cases} $ |
| $(c):$ |
測定
${\mathsf M}_{C({}\Omega{})} ({}{\mathsf O}_1, S_{[{}\ast{}]})$により,
測定値「3」を得る
$ \Leftrightarrow \begin{cases} \textcolor{magenta}{ \mbox{司会者が「ドア$A_3$の後ろに 『羊』がいる」と言う } } \\ \textcolor{blue}{ \mbox{皇帝が「囚人$A_3$ は死刑になる」と言う } } \end{cases} $ |
さて, 問題9.21(モンティホール問題) [resp. 問題9.22(三囚人の問題) ]では, 上の(c)の場合なので、 すなわち、 「測定 ${\mathsf M}_{C({}\Omega{})} ({}{\mathsf O}_1, S_{[{}\ast{}]})$により, 測定値「3」を得る」 を意味する. ここで,次に注意しよう. \begin{align} & [F_1({}\{3\}{})] ({}\omega_2{}) = 1.0 = \max \{ 0.5, \; \; 1.0 , \; \; 0.0 \} \nonumber \\ & = \max \{ [F_1({}\{3\}{})] ({}\omega_1{}), [F_1({}\{3 \}{}){}]({}\omega_2{}), [F_1({}\{3 \}{})] ({}\omega_3{}) \}, \tag{9.30} \end{align} したがって,フィッシャーの最尤法によって,
| $(B_1):$ | 問題9.21(モンティホール問題) では, $[\ast]$ $=$ $\delta_{\omega_2}$と推論する理由がある. よって, あなたは,ドア$A_2$に変更するべきである. |
| $(B_2):$ |
問題9.22(三囚人の問題)
でも,
$[\ast]$
$=$
$\delta_{\omega_2}$と推論する理由がある.
しかしながら,
「囚人$A_1$の幸福度が増したか減じたのか」の(フィッシャー統計での)合理的な答えはない.
問題9.22(三囚人の問題)は,
|