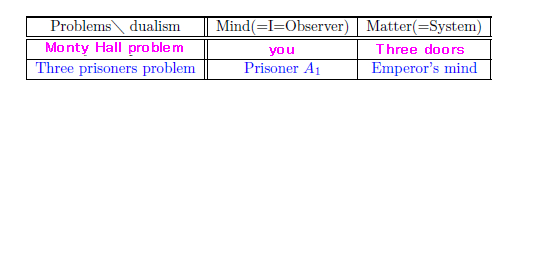
二元論(物心二元論)の対立関係
離散距離空間$\Omega$を
$\Omega = \{ \omega_{1} , \omega_{2} , \omega_{3} \}$
とする.
ここで,各状態
$\delta_{\omega_{{m}}}
(\in
{\frak S}^p (C(\Omega)^* ))$
は,次を意味するとする.
$C(\Omega)$内の観測量
${\mathsf O}_1$
$\equiv$
$({}\{ 1, 2,3 \}, 2^{\{1, 2 ,3\}}, F_1)$を以下のように定める.
問題9.23の仮定$(\sharp_1)$
[resp.
問題9.24の仮定$(\sharp_2)$
]
より,混合状態$\nu_0(\in {\frak S}^m(C(\Omega)^* ))$
は
\begin{align*}
\nu_0 = p_1 \delta_{\omega_1} + p_2 \delta_{\omega_2}+p_3 \delta_{\omega_3}
\end{align*}
さて,
問題9.21(モンティホール問題)
[resp.
問題9.22(三囚人の問題)
]では,
上の(c)の場合なので、
すなわち、
「測定
${\mathsf M}_{C({}\Omega{})} ({}{\mathsf O}_1, S_{[{}\ast{}]}(\nu_0))$により,
測定値「3」を得る」
を意味する.
したがって,
ベイズの方法
より,
事後状態$\nu_{\rm post}$
$({}\in {\cal M}_{+1}^m ({}\Omega{}){})$
は次のようになる.
9.10: ベイズ統計学:
モンティ・ホール問題
[resp.
三囚人の問題
]
This section is extracted from
following:
$(\sharp):$
S. Ishikawa;
Final Solutions of Monty Hall problem and Three Prisoners Problem
arXiv:1408.0963v1 [stat.OT] 2014
9.10: ベイズ統計学:
モンティ・ホール問題
[resp.
三囚人の問題
]
$\quad$
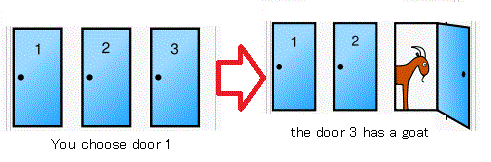
あなたはゲームショウに参加している.三つのドア
(i.e., ドア$A_1$, ドア$A_2$, ドア$A_3$)があって,
一つのドアの後ろには『自動車』が,
また他の二つのドアの後ろには『羊』が隠されている. 司会者はドアの後ろが見えるが,あなたには見えない.
司会者が,「どのドアの後ろに,『自動車』が隠されていると思いますか?」
とあなたに問う.ゲームなので,あなたは
「ドア$A_1$」と答えたとしよう.
そして,司会者は次のように言った.
さらに,司会者は「ドア$A_3$の後ろは,『羊』ですよ」とあなたに教えてくれた.
最後に,司会者は
「あなたは,ドア$A_1$と言ってしまいましたが,いまからでも,ドア$A_2$に変更できますよ」と言った.さて,ここで,
$(\sharp_1):$
どのドアの後ろに『自動車』を置くかは,
(公正とは限らない)サイコロ投げで決めた.
すなわち、各ドア$A_m$の後ろに,『自動車』が置いてある確率は,
$p_m$
(ここに、
$p_1 + p_2 + p_3 =1$, $ 0 \le p_1 , p_2 , p_3 \le 1 $
$)$
である.
$\bullet$
あなたは,ドア$A_1$のままにして変更しないか,または,ドア$A_2$に変更しますか?
$\quad$
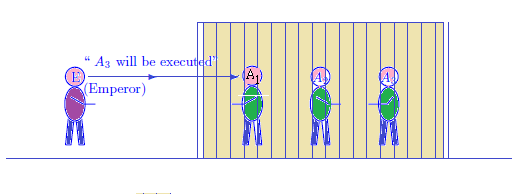
三人の死刑囚$A_1$, $A_2$と$A_3$が牢屋に入っている.
皇帝によって,三人の内の一人は恩赦で,罪を許された.
恩赦された者が誰だかは,皇帝は知っているが,三人には知らされていない.
ここで,囚人$A_1$が皇帝に次のように言った.
「 私以外の二人の内で,すくなくとも一人は,死刑のはず.
その一人を私だけに教えてくれませんか?」
皇帝はすこし考えたが,
「囚人$A_1$には,関係ないことなので,いいか」と思って,
「$A_3$さんは死刑だよ」
と答えた.またさらに,
と言った.
そこで, 囚人$A_1$は次のように考えた.
$(\sharp_1):$
誰を恩赦にするかは,(公正とは限らない)サイコロ投げで決めた.
すなわち,$A_m$さんが、恩赦される確率は
$p_m$
(where
$p_1 + p_2 + p_3 =1$, $ 0 \le p_1 , p_2 , p_3 \le 1 $
$)$
であった.
ここで,問題は
$\bullet$
もともとは,3人の内で一人が恩赦だったのに,
$A_3$さんは死刑確定で,結局,二人の内で一人になったのだから,
ラッキーと考えた.
である.
$\bullet$
この$A_1$さんは本当にラッキーになったのだろうか?
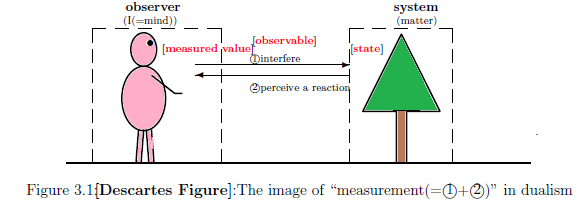
デカルト図式を確認しよう。
となり,
混合測定
${\mathsf M}_{C(\Omega )} ({\mathsf O}_1, S_{[\ast ]}(\nu_0))$
を得る.
である.
$\bullet$
$\quad$
$
\begin{cases}
\textcolor{magenta}{
\mbox{
あなたが「ドア$A_1$」と言う
}
}
\\
\textcolor{blue}{
\mbox{
「囚人$A_1$」が皇帝に「他の二人のどっちが死刑か?」と問う
}
}
\end{cases}
$
$(a):$
測定
${\mathsf M}_{C({}\Omega{})} ({}{\mathsf O}_1, S_{[{}\ast{}]}(\nu_0))$により,
測定値「1」を得る
$
\Leftrightarrow
\begin{cases}
\textcolor{magenta}{
\mbox{司会者が「ドア$A_1$の後ろに
『羊』がいる」と言う
}
}
\\
\textcolor{blue}{
\mbox{皇帝が「囚人$A_1$
は死刑になる」と言う
}
}
\end{cases}
$
$(b):$
測定
${\mathsf M}_{C({}\Omega{})} ({}{\mathsf O}_1, S_{[{}\ast{}]}(\nu_0))$により,
測定値「2」を得る
$
\Leftrightarrow
\begin{cases}
\textcolor{magenta}{
\mbox{司会者が「ドア$A_2$の後ろに
『羊』がいる」と言う
}
}
\\
\textcolor{blue}{
\mbox{皇帝が「囚人$A_2$
は死刑になる」と言う
}
}
\end{cases}
$
$(c):$
測定
${\mathsf M}_{C({}\Omega{})} ({}{\mathsf O}_1, S_{[{}\ast{}]}(\nu_0))$により,
測定値「3」を得る
$
\Leftrightarrow
\begin{cases}
\textcolor{magenta}{
\mbox{司会者が「ドア$A_3$の後ろに
『羊』がいる」と言う
}
}
\\
\textcolor{blue}{
\mbox{皇帝が「囚人$A_3$
は死刑になる」と言う
}
}
\end{cases}
$
$(B'_1):$
問題9.23(モンティ・ホール問題)
では
\begin{align*}
\begin{cases}
\mbox{
もし
$\nu_{\rm post} ({}\{ \omega_1 \}{})$
$<$
$\nu_{\rm post} ({}\{ \omega_2 \}{})$
(i.e., $p_1 < 2 p_2 $)ならば,
あなたは
ドア$A_2$を選ぶべき}
\\
\mbox{
もし
$\nu_{\rm post} ({}\{ \omega_1 \}{})$
$=$
$\nu_{\rm post} ({}\{ \omega_2 \}{})$
(i.e., $p_1 = 2 p_2 $)ならば,
どちらでも可}
\\
\mbox{
もし
$\nu_{\rm post} ({}\{ \omega_1 \}{})$
$>$
$\nu_{\rm post} ({}\{ \omega_2 \}{})$
(i.e., $p_1 > 2 p_2 $)ならば,あなたは
ドア$A_1$を選ぶべき}
\end{cases}
\end{align*}
となる
$(B'_2):$
問題9.24(三囚人問題)
では,
\begin{align*}
\begin{cases}
\mbox{
もし$
\nu_{0} (\{\omega_1\})
< \nu_{\rm post} (\{\omega_1\})$
(i.e., $p_1 < 1- 2 p_2$)ならば,
囚人$A_1$の幸福度は増大
}
\\
\mbox{
もし$
\nu_{0} (\{\omega_1\})
=
\nu_{\rm post} (\{\omega_1\})$
(i.e., $p_1 = 1- 2 p_2$)ならば,
囚人$A_1$の幸福度は不変}
\\
\mbox{
もし$
\nu_{0} (\{\omega_1\})
> \nu_{\rm post} (\{\omega_1\})$
(i.e., $p_1 > 1- 2 p_2$)ならば,
囚人$A_1$の幸福度は減少}
\\
\end{cases}
\end{align*}
9.10:ベイズ統計学: モンティ・ホール問題と三囚人問題
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
問題9.23[(=問題9.16)Monty Hall 問題(ベイス統計)].
問題9.24 [三囚人の問題: ベイズ統計]
9.10.2: 解答(ベイズ統計学):
モンティ・ホール問題
[resp.
三囚人の問題
]
「測定
${\mathsf M}_{C({}\Omega{})} ({}{\mathsf O}_1, S_{[{}\ast{}]})$を行う」
とは,
したがって,次の対応を考える.
