半径$1$の円がある。
この円から、「無作為」に一つの弦$\ell$を選ぼう。
このとき、その弦の長さが$\sqrt{3}$以下である確率を求めよ。
回転写像 $T_{\mbox{rot}}^\theta : {\mathbb R}^2 \to {\mathbb R}^2$
$(- \pi \le \theta \le \pi)$
と
裏返し写像
$T^\theta_{\mbox{rev}} : {\mathbb R}^2 \to {\mathbb R}^2$
を以下のように定める。
\begin{align*}
&
T_{\mbox{rot}}^\theta \left[\begin{array}{ll}
x_1 \\
x_2
\end{array}\right] =
\left[\begin{array}{ll}
\cos \theta & - \sin \theta \\
\sin \theta & \cos \theta
\end{array}\right]
\cdot
\left[\begin{array}{ll}
x_1 \\
x_2
\end{array}\right] ,
\quad
T^\theta_{\mbox{rev}} \left[\begin{array}{ll}
x_1 \\
x_2
\end{array}\right] =
T_{\mbox{rot}}^\theta
\left[\begin{array}{ll}
0 & 1 \\
1 & 0
\end{array}\right]
T_{\mbox{rot}}^{-\theta}
\left[\begin{array}{ll}
x_1 \\
x_2
\end{array}\right]
\end{align*}
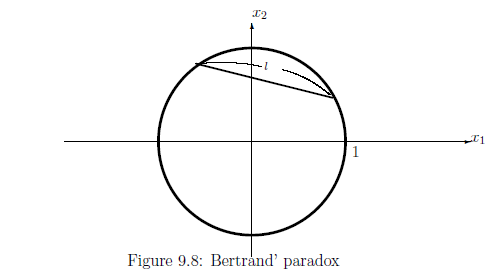
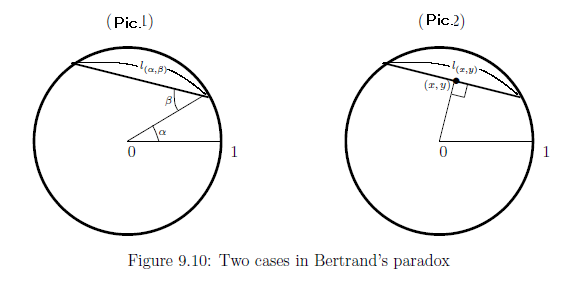
Pic.$1$において,
弦$\ell$の座標表示を
長方形$\Omega_1$
$\equiv$
$\{ ({}\alpha, \beta{}) \; | \; 0 < \alpha \le 2 \pi, \;
0 < \beta \le \pi/2 \text{(radian)}\}$
内の点
$({}\alpha, \beta{}) $
で表す。
すなわち、次の同一視を考える。
したがって、
自然な確率測度
$\nu_1$
$( \in {\mathcal M}_{+1}(\Omega_1))$を
次のように定めることができる:
ここに、
"Meas"
はルベーグ測度.
確率測度
$\nu_1$
$( \in {\mathcal M}_{+1}(\Omega_1))$を
$\Omega$へ移して,
確率測度
$\rho_1$
$( \in {\mathcal M}_{+1}(\Omega_1))$
を定める.
すなわち,
ここで、
したがって、この$(\sharp)$の意味で、「自然」な精密測定
${\mathsf M}_{L^\infty ( \Omega, \rho_1 )}({\mathsf O}_E \equiv
(\Omega, {\mathcal B}_{\Omega} , F_E), {\overline S}_{[\ast]}(1) )$
を得る。
次の同一視:
の下に、
混合言語ルール$^{\mbox{(m)}}$ 1 ($\S$9.1)
の主張は、
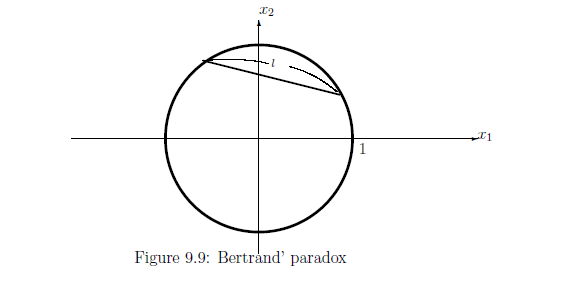
Pic.$2$において,
弦$\ell$の座標表示を
円盤$\Omega_2$
$\equiv$
$\{ (x,y) \; | \;
x^2 + y^2 < 1
\}$内の点
$(\alpha, \beta) $
で表す。
すなわち、次の同一視を考える。
したがって、
自然な確率測度
$\nu_2$
$(\in {\mathcal M}_{+1}( \Omega_2))$を、次のように定めることができる。
確率測度
$\nu_2$
$(\in {\mathcal M}_{+1}( \Omega_2))$を
$\Omega$上の確率測度
$\rho_2$に移して、
すなわち、
したがって、この$(\sharp)$の意味で、「自然」な精密測定
${\mathsf M}_{L^\infty ( \Omega, \rho_2 )}({\mathsf O}_E \equiv
(\Omega, {\mathcal B}_{\Omega} , F_E), {\overline S}_{ [\ast]}(1) )$
を得る。
次の同一視:
の下に、
混合言語ルール$^{\mbox{(m)}}$ 1 ($\S$9.1)
の主張は、
自然な確率測度
(すなわち、
回転写像 $T_{\mbox{rot}}^\theta : {\mathbb R}^2 \to {\mathbb R}^2$
$(- \pi \le \theta \le \pi)$
と
裏返し写像
$T^\theta_{\mbox{rev}} : {\mathbb R}^2 \to {\mathbb R}^2$
に関して、不変な確率測度
)
を「ランダム(とか、無作為)」と見なす習慣があるとしても、
第一の解答と
第二の解答によって、次が言える。
定理9.18(等重率)は,
と主張していると思うかもしれない.しかし,定理9.18(等重率)内でも断ったように,
このランダムの意味は,
$\bullet$
状態空間が有限ならば,ランダム(=無作為)が意味を持つ
すなわち、
である.
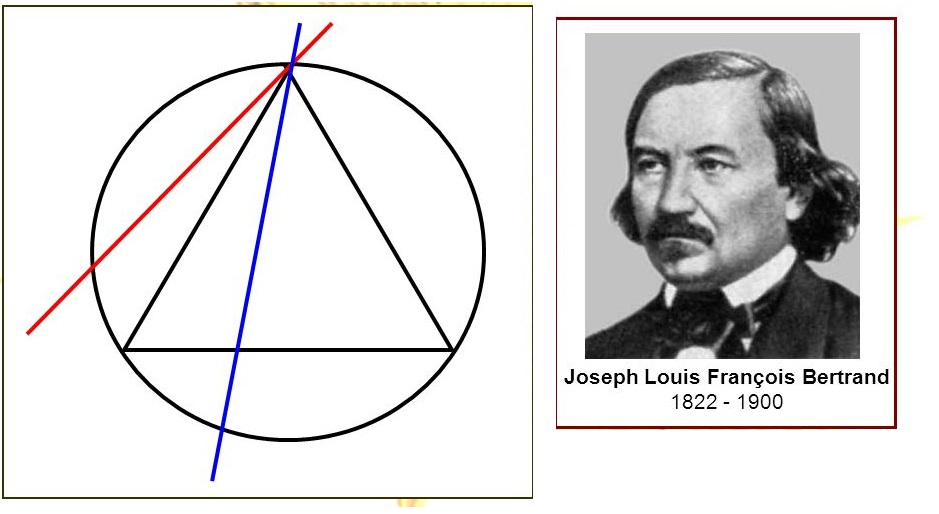
「意味づけ無し」の「無条件なランダム」などは無い.このことは,「ベルトランのパラドックス」として知られている. 以下にこれを説明しよう.
9.12.1: ベルトランのパラドックス(「ランダム」は見方次第)
さて、
ベルトランのパラドックスを復習しよう。
半径$1$の円が、以下のように与えられている。
$\Omega$
$=\{l \;|\; l \mbox{ は弦} \}$,
すなわち,
弦全体の集合
として、次を考える。
$(A):$
$\Omega$上の確率測度で、不変な(すなわち、
回転写像 $T_{\mbox{rot}}^\theta : {\mathbb R}^2 \to {\mathbb R}^2$
$(- \pi \le \theta \le \pi)$
と
裏返し写像
$T^\theta_{\mbox{rev}} : {\mathbb R}^2 \to {\mathbb R}^2$
に関して、不変な
)
測度は
一意に
存在するか?
[第一の解答 (Pic.$1$(in Figure 9.10))]
$(\sharp):$
確率測度$\rho_1 (\in {\mathcal M}_{+1}(\Omega ))$
は、不変な(すなわち、
回転写像 $T_{\mbox{rot}}^\theta : {\mathbb R}^2 \to {\mathbb R}^2$
$(- \pi \le \theta \le \pi)$
と
裏返し写像
$T^\theta_{\mbox{rev}} : {\mathbb R}^2 \to {\mathbb R}^2$
に関して、不変な
)
測度である。
$\bullet$
測定値が
$\Xi_{\sqrt{3}}$
に属する確率は
\begin{align}
&
\int_{\Omega} [F_E (\Xi_{\sqrt{3}})](\omega) \; \rho_1( d \omega )=
\int_{\Xi_{\sqrt{3}}}\;\; 1 \;\; \rho_1( d \omega )
\\
=
&
m_1
(\{ \ell_{({}\alpha , \beta{})} \approx (\alpha, \beta) \in \Omega_1 \; | \;
\mbox{ "the length of } \ell_{({}\alpha , \beta{})}" \le {\sqrt 3} \}{})
\\
=
&
\frac{\text{Meas}[{}\{ ({}\alpha, \beta{}) \; | \; 0 \le \alpha \le 2 \pi,
\;\pi/6 \le \beta \le \pi/2 \}]}
{\mbox{
Meas}[{}\{ ({}\alpha, \beta{}) \; | \; 0 \le \alpha \le 2 \pi,
\;0 \le \beta \le \pi/2\}]}
\\
=
&
\frac{2 \pi \times ( \pi/3)}
{\pi^2}
= \frac{2}{3}.
\end{align}
となる。

[第二の解答 (Pic.$2$(in Figure 9.10))].
$(\sharp):$
確率測度$\rho_2 (\in {\mathcal M}_{+1}(\Omega ))$
は、不変な(すなわち、
回転写像 $T_{\mbox{rot}}^\theta : {\mathbb R}^2 \to {\mathbb R}^2$
$(- \pi \le \theta \le \pi)$
と
裏返し写像
$T^\theta_{\mbox{rev}} : {\mathbb R}^2 \to {\mathbb R}^2$
に関して、不変な
)
測度である。
$\bullet$
測定値が
$\Xi_{\sqrt{3}}$
に属する確率は
\begin{align*}
&
\int_{\Omega} [F_E (\Xi_{\sqrt{3}})](\omega) \; \rho_2( d \omega )=
\int_{\Xi_{\sqrt{3}}}\;\; 1 \;\; \rho_2( d \omega )
\\
=
&
\nu_2
(\{ \ell_{({}x,y)} \approx (x,y) \in \Omega_2 \; | \;
\text{"the length of } \ell_{(x,y)}" \le {\sqrt 3} \}{})
\\
=
&
\frac{\text{Meas} [{}
\{ (x,y) \; | \; 1/4 \le x^2+y^2 \le 1 \}
]}
{\pi}
= \frac{3}{4}.
\end{align*}
となる。
すなわち、
$(\sharp):$
$\quad$問題9.28の「一意性」は否定される。
とか、
である。
そうならば、一意性は言えない
補足:
この節では、量子言語の立場から、「ベルトランの逆理」について議論したが、
別に「新しい知見」を述べたわけではない。
などは、まともな研究者(または、素人でも)ならば、常識的なことと思う。
「ベルトランのパラドックスは、不可解な未解決問題」などと信じている研究者は、すくなくても著者の周りにはいない。
しかしながら、
かもしれない。
たとえば、 「下図のようなサイコロを1000回投げる自由研究」をやっている中学生とか。
9.12: ベルトランのパラドックス(「ランダム」は見方次第)
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
問題9.27(ベルトランのパラドックス)
問題9.28 (ベルトランのパラドックスとその解答)
$\square \quad$
結論9.29
