質量$m$の粒子$P$が箱
(i.e.,
閉区間$[0,2](\subseteq {\mathbb R} )$)
の中に入っている.
この粒子$P$の波動関数は次のシュレーディンガー方程式で表される.
ここに
10.5: 演習:シュレーディンガー方程式を変数分離法で解く
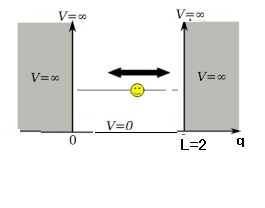
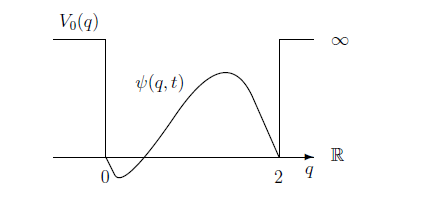
さて,
と置いて,これをシュレーディンガー方程式に代入して,
\begin{align} i \hbar \frac{\partial}{\partial t } \phi (q ,t) = - \frac{\hbar^2 \partial^2}{2 m \partial q^2 }\phi (q ,t). \end{align}次を得る.
\begin{align} \frac{i T' (t) }{T(t)} =- \frac{ X'' (q)}{2 m X(q) } = K (= \mbox{ constant }). \end{align}これを計算して,
\begin{align} \phi (q, t) = T(t)X(q) = C_3 \exp (iKt) \Big(C_1 \exp(i \sqrt{2mK/\hbar} \; q) + C_2 \exp(-i \sqrt{2mK/\hbar} \; q). \Big) \end{align}境界条件は$X(0)=X(2)=0$を考慮して, $K= \frac{n^2 \pi^2 \hbar}{8 m}$ とすると,
\begin{align} \phi (q, t) = T(t)X(q) = C_3 \exp (\frac{ i n^2 \pi^2 \hbar t}{8 m}) \sin(n \pi q / 2) \qquad (n=1,2,...). \end{align}初期条件を
\begin{align} \psi(q,0) = c_1 \sin (\pi q / 2) + c_2 \sin (2 \pi q / 2) + c_3 \sin (3 \pi q / 2) + \cdots. \end{align}ここに、 $\int_{\mathbb R} | \psi(q , 0)|^2 dq = 1$. として,つぎの波動関数を得る.
\begin{align} & \psi(q,t) \\ = & c_1 \exp (\frac{ i \pi^2 \hbar t}{8 m}) \sin (\pi q / 2) + c_2 \exp (\frac{ i 4 \pi^2 \hbar t}{8 m}) \sin (2 \pi q / 2) + c_3 \exp (\frac{ i 9 \pi^2 \hbar t}{8 m}) \sin (3 \pi q / 2) + \cdots. \end{align}
よって、次のシュレーディンガー描像を得る。
