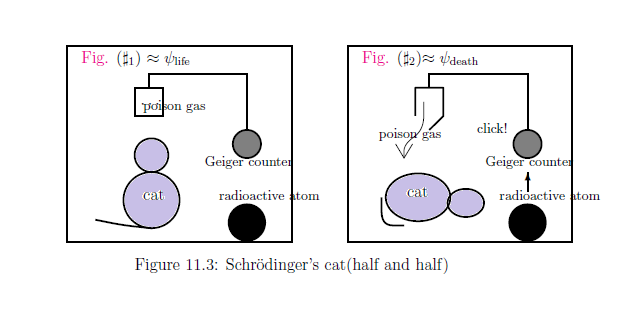
「シュレーディンガーの猫」のパラドックスを,
シュレーディンガー描像の下に説明する.
「シュレーディンガーの猫」
は
量子力学で最も有名なパラドックスである.
これを問題形式で説明する.
問題11.11 [シュレーディンガーの猫]
| $(a):$ |
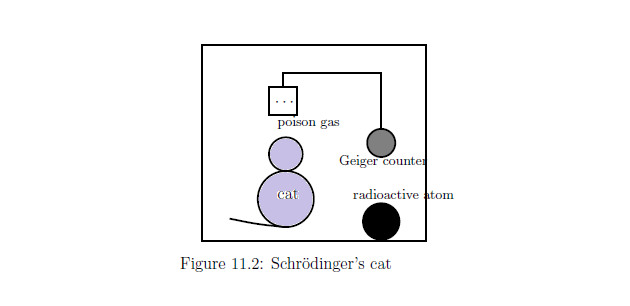
箱の中に猫を入れておく.
放射性元素,ガイガーカウンター,毒ガスの入っている小さい箱も入れておく.
1時間後に放射性元素からは放射能が出る可能性は
半々
とする.
もし放射能が出ると,ガイガーカウンターが
鳴って,それが引き金になって
毒ガスの入っている小さい箱の扉が開く.
そうすれば,毒ガスが充満して,必然的に猫が死ぬという
仕掛けである.
また,放射能が出なければ,猫は
元気に生きているというわけである.
もちろん,箱の窓は閉じているので,あなたは猫がどうなっているのか
を知らない。
|
さて,ここで次の問題を考えよう:
| $(b):$ |
一時間後に、あなたが箱の中を見たとして,猫はどうなっているのだろうか?
生きているのか?
死んでいるのか?
もちろん,
「半々」
に違いないが,この
「半々」
の意味を明確にせよ.
|
| $\fbox{注釈11.1}$ |
[ウィグナーの友人]:
上の(b)の代わりに
| $(b'):$ |
一時間後に、「ウィグナーの友人」が箱の中を見たとして,それを
さらに一時間後にあなたに伝えたとする。
「ウィグナーの友人」が箱の中を見たときとか
それを「ウィグナーの友人」があなたに伝えたときとかに、
猫はどうなっているのだろうか?
|
一見、難問と思うかもしれないが、言語的解釈では「測定した瞬間」という概念がないのだから、(b$'$)は量子言語で記述できない。
言語的科学観の精神(ウィトゲンシュタインの言葉)
-
The limits of my language mean the limits of my world
(言語の限界が世界の限界)
とか
-
What we cannot speak about we must pass over in silence
(語り得ぬことには、沈黙せねばならない)
を思い出そう。
|
11.5.2: 通常の解答
解答 11.12 [通常の解答 (i.e.,量子言語を使わない解答)].
${\mathbf q}=(q_{11}, q_{12}, q_{13}, q_{21},q_{22}, q_{23}, \dots, q_{n1},q_{n2}, q_{n3} ) \in {\mathbb R}^{3n} $として,
\begin{align*}
\nabla_i^2
=
\frac{\partial^2}{\partial q_{i1}^2}
+
\frac{\partial^2}{\partial q_{i2}^2}
+
\frac{\partial^2}{\partial q_{i3}^2}
\end{align*}
と定めて,量子系の基本構造:
\begin{align*}
{\mathcal C}(H)
\subseteq
B(H)
\subseteq
B(H)
\qquad
\mbox{
(
ここで,$H=L^2 ( {\mathbb R}^{3n}, d {\mathbf q} )$とする
)}
\end{align*}
内で,多粒子系($n$個の粒子系)のシュレーディンガー方程式:
\begin{align}
\begin{cases}
i \hbar \frac{\partial}{\partial t} \psi ( {\mathbf q}, t )
=
\Big[
\sum_{i=1}^n \frac{- \hbar^2}{2m_i} \nabla_i^2 + V( {\mathbf q}, t )
\Big]
\psi ( {\mathbf q}, t )
\\
\\
\psi_0({\mathbf q})=\psi ( {\mathbf q}, 0 ):
\mbox{初期条件}
\end{cases}
\tag{11.16}
\end{align}
を考える.ここに,$m_i$は粒子$P_i$の質量,$V$はポテンシャルエネルギーとする.
量子力学を
信じるとしたならば,上のシュレーディンガー方程式(11.16)を解けばよい.
すなわち,
| $(A_1):$ |
一時間後($t=60^2$秒後)の$\psi( {\mathbf q}, 60^2 )$が計算できたとしよう.
したがって,一時間後の箱の中の状態は,
$\rho_{60^2}$
$(\in {\mathcal Tr}_{+1}^p (H)
)$
は
\begin{align}
\rho_{60^2}=
|
\psi_{60^2}
\rangle
\langle
\psi_{60^2}
|
\tag{11.17}
\end{align}
となる
(ここに,
$
\psi_{60^2}
=
\psi(\cdot , 60^2 )
$).
|
さて,$B(H)$内の次は観測量${\mathsf O}=
(X=\{生, 死\},
2^X, F)$を次のように定める.
| $(A_2):$ |
つまり,
\begin{align*}
&
V_{生} (\subseteq H )
=
\Big\{ u\in H \;|\; "箱内の状態は\frac{|u\rangle \langle u |}{\|u\|^2}" \Leftrightarrow
\mbox{"猫は生きている”}
\Big\}
\\
&
V_{死} (\subseteq H )=V_{生}\mbox{の直交補空間}
\end{align*}
として,
$F(\{生\})(\in B(H) )$は閉部分空間$V_{生}$への射影作用素,また,$F(\{死\})=I - F(\{生\})$,
すなわち,
閉部分空間$V_{死}$への射影作用素
と定める.
|
ここで,
| $(A_3):$ |
測定${\mathsf M}_{B(H)}({\mathsf O}=(X, 2^X, F), S_[\rho_{60^2}])$を考える.
測定値
「生」,「死」を得る確率は,
「半々」
なのだから,
\begin{align*}
&
{}_{{\mathcal Tr}(H)}
\Big(\rho_{60^2}, F(\{生\}) \Big){}_{B(H)}=\langle
\psi_{60^2},F(\{生\})\psi_{60^2} \rangle=0.5
\\
&
{}_{{\mathcal Tr}(H)}
\Big(\rho_{60^2}, F(\{死\}) \Big){}_{B(H)}=\langle
\psi_{60^2},F(\{死\})\psi_{60^2} \rangle=0.5
\end{align*}
となるはずである.
|
そうだとしたら,
\begin{align}
&
\psi_{60^2}= \frac{1}{\sqrt 2}( \psi_{生}+ \psi_{死})
\tag{11.18}
\\
(ここに,
&
\psi_{生}\in V_{生},\|\psi_{生}\|=1
\quad
\psi_{死}\in V_{死},\|\psi_{死}\|=1
)
\nonumber
\end{align}
と表現されるはずである.
次が結論できる.
| $(A4):$ |
一時間後に,猫は「(11.18)式の意味で半死半生」の状態である。
誤解を恐れずに書くならば,
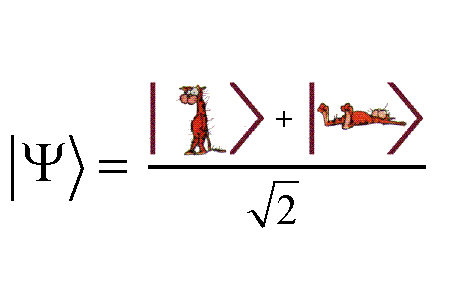 \begin{align*}
\frac{
\text{" 図$(\sharp_1)$"} +
\text{" 図($\sharp_2$)"}
}{\sqrt{2}}
\end{align*}
のような状態である.
\begin{align*}
\frac{
\text{" 図$(\sharp_1)$"} +
\text{" 図($\sharp_2$)"}
}{\sqrt{2}}
\end{align*}
のような状態である.
|
そして,
| $(A5):$ |
一時間後に,箱の窓を開けて中を見た瞬間(すなわち,測定した瞬間)に,
「元気に生きている」か
「死んでいる」かのどちらかが決定する.すなわち,
\begin{align*}
半死半生(=\frac{1}{2}(|\psi_{生}+ \psi_{死}\rangle \langle \psi_{生}+ \psi_{死}|))
\xrightarrow[\textcolor{red}{波動関数の収縮が起きる}]{\textcolor{red}{測定した瞬間に}}
\begin{cases}
元気に生きている(=|\psi_{生}\rangle \langle \psi_{生}|)
\\
\\
死んでいる(=|\psi_{死}\rangle \langle \psi_{死}|)
\end{cases}
\end{align*}
|
となる.
$\square \quad$
11.5.3: 量子言語による解答
解答 11.13 [量子言語による解答]
量子言語では量子デコヒーレンスを認めるので,,
| $(B_1):$ |
時間発展して,一時間後には
$
\rho'_{60^2}
$
は,
\begin{align*}
\rho'_{60^2}
=
\frac{1}{2}
\Big(
|
\psi_{生}
\rangle
\langle
\psi_{生}
|
+
|
\psi_{死}
\rangle
\langle
\psi_{死}
|
\Big)
\end{align*}
のような混合状態になったとしてもよい.
|
ここで,
| $(B_2):$ |
測定${\mathsf M}_{B(H)}({\mathsf O}=(X, 2^X, F), S_{[\ast]}(\rho'_{60^2}))$を考える.
測定値
「生」,「死」を得る確率は,
\begin{align*}
&
{}_{{\mathcal Tr}(H)}
\Big(\rho'_{60^2}, F(\{生\}) \Big){}_{B(H)}=\langle
\psi_{60^2},F(\{生\})\psi_{60^2} \rangle=0.5
\\
&
{}_{{\mathcal Tr}(H)}
\Big(\rho'_{60^2}, F(\{死\}) \Big){}_{B(H)}=\langle
\psi_{60^2},F(\{死\})\psi_{60^2} \rangle=0.5
\end{align*}
となる.
|
もっと正確には,
非決定的因果作用素
$\Phi: B(H) \to B(H)$
を
$$
(\Phi)_* \rho_0 = \rho'_{60^2}
$$
のように定めて、
| $(B_3):$ |
測定${\mathsf M}_{B(H)}(\Phi{\mathsf O}=(X, 2^X, \Phi F), S_{[\rho_0]})$を考える.
測定値
「生」,「死」を得る確率は,
\begin{align*}
&
{}_{{\mathcal Tr}(H)}
\Big(\rho_{0}, \Phi F(\{生\}) \Big){}_{B(H)}=
{}_{{\mathcal Tr}(H)}
\Big(\rho'_{60^2}, F(\{生\}) \Big){}_{B(H)}=\langle
\psi_{60^2},F(\{生\})\psi_{60^2} \rangle=0.5
\\
&
{}_{{\mathcal Tr}(H)}
\Big(\rho_{0}, \Phi F(\{死\}) \Big){}_{B(H)}=
{}_{{\mathcal Tr}(H)}
\Big(\rho'_{60^2}, F(\{死\}) \Big){}_{B(H)}=\langle
\psi_{60^2},F(\{死\})\psi_{60^2} \rangle=0.5
\end{align*}
となる.
|
また,
「測定した瞬間」とか「波動関数の収縮」とかは,量子言語では禁忌であるが,($B_3$)は言える.
$\square \quad$
11.5.4: 要約 (Laplace's demon)
要約 11.14 [シュレーディンガーの猫の量子言語的総括]
さて,
-
解答11.12(通常解答)
v.s.
解答11.13(量子言語による解答)
を検討しよう.
| $(C_1):$ |
通常の解答(A5)を主張して,頑張れば頑張り切る
|
としても,やはり気が引ける.
妥当な線としては,次だろう.
| $(C_2):$ |
いかなる理論にも,「適用範囲」ある.
たとえば,
| $\bullet$ |
ニュートン力学を宇宙全体に適用すれば,「ラプラスも魔(
cf.
注釈12.1
)」
になって,無理が生じる.
ニュートン力学を微細な世界に適用すれば,カオスが発生して,訳がわからない現象が現れる.これらは,ニュートン力学の適用範囲外
|
が妥当と考える.
| $\bullet$ |
適用範囲外の場合の有効な対処法としては,ブラウン運動(確率微分方程式)を用いる方法であるが,これはニュートン力学を拡大解釈して(すなわち,動的システム理論と考えて),すでに物理学からは離れた理論であることに注意すべきである.すなわち,
\begin{align}
\underset{\mbox{物理学}}{
\fbox{ニュートン力学}
}
\xrightarrow[\mbox{言語的転回}]{\mbox{適用範囲外}}
\underset{\mbox{形而上学}}{
\fbox{動的システム理論;統計学}
}
\tag{11.19}
\end{align}
|
そうだとしたら,
量子力学にも「適用範囲」があると考えるのは自然だろう.すなわち,
| $\bullet$ |
シュレーディンガの猫は量子力学(特に,シュレーディンガー方程式)の適用範囲外
|
が妥当と考える.
| $\bullet$ |
適用範囲外の場合の有効な対処法としては,($B_3$)のような量子デコヒーレンスを用いる方法であるが,これは量子力学を拡大解釈して(すなわち,量子システム理論と考えて),すでに物理学からは離れた理論であることに注意すべきである.
|
|
以上,
($C_1$)でもよいが,($C_2$)を推奨したい.なぜならば,
| $(C_3):$ |
次の二つの理論:
| $\bullet$ |
ニュートン力学を拡大解釈して(すなわち,動的システム理論と考えて),すでに物理学からは離れた理論
|
| $\bullet$ |
量子力学を拡大解釈して(すなわち,量子システム理論と考えて),すでに物理学からは離れた理論
|
を一つに統合した理論こそ,量子言語だからである.
|
以上のように,
シュレーディンガーの猫は,量子言語が無くては,解決しないと考えるので,
($C_2$)を推奨したい.
| $\fbox{注釈11.3}$ |
[ラプラスの魔]:
宇宙全体のすべての物体の運動でも
国の経済成長でも,
所詮は,(無限に近い)多数の粒子系の運動方程式で
厳密に記述できて,しかも,
それを解析することができる知性が存在するならば,
この知性にとっては,
不確実なことは何もなくなり,その目には未来も過去も
全て見えていると考えて,
このような「知性」のことを
ラプラスの魔
と呼ぶ.
ラプラスの魔は,
「度が過ぎた実在的科学観
(すなわち,極端な物理至上主義)」
の象徴として,
しばしば議論される.すなわち、
\begin{align}
\underset{\mbox{物理学}}{
\fbox{ニュートン力学}
}
\xrightarrow[\mbox{極端な物理至上主義}]{\mbox{適用範囲外}}
\underset{\mbox{物理学?}}{
\fbox{ラプラスの魔}
}
\tag{11.20}
\end{align}
で、これと式(11.19)は比較されるべきであるが、科学の常識は、式(11.19)を選んだ。
|
}
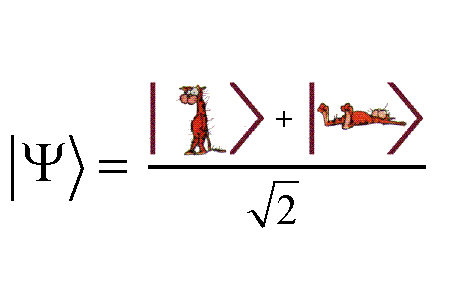 \begin{align*}
\frac{
\text{" 図$(\sharp_1)$"} +
\text{" 図($\sharp_2$)"}
}{\sqrt{2}}
\end{align*}
のような状態である.
\begin{align*}
\frac{
\text{" 図$(\sharp_1)$"} +
\text{" 図($\sharp_2$)"}
}{\sqrt{2}}
\end{align*}
のような状態である.