11.6: 語り得ぬことには、沈黙しなければならない
この節は、次の論文からの抜粋である:
11.6.1: 「粒子か? 波か?」は愚問
旧来の量子力学では、
「粒子か波か?」という問いかけが頻繁にされている。
しかし、
次表に見るように
この問いかけは愚問である。
この表11.1
で、一番理解し易いのは、ニュートン力学
(i.e.,
質点 $\leftrightarrow$ 状態) である。
これが分かれば、他も容易に理解できると思う。
量子力学では、
「粒子か波か?」という問いかけが、
ウィーラーの遅延選択測定との関係で議論されることが多い。
したがって、
この節では、
| $(A1):$ |
ウィーラーの遅延選択測定を量子言語で記述する
|
ことを考える。結論的には
| $(A2):$ |
ウィーラーの遅延選択測定をパラドック風には量子言語で記述することはできない
|
と結論して、結局、
| $(A3):$ |
語り得ぬことには、沈黙しなければならない
|
とウィトゲンシュタインを気取る。
11.6.2: 準備
$H$を2次元ヒルベルト空間,
すなわち,
$H={\mathbb C}^2$
とする.
ここで,
基本構造$[{\mathcal C}(H), B(H )]_{B(H )}]$を
\begin{align*}
[{\mathcal C}(H ), B(H )]_{B(H)}
=
[B({\mathbb C}^2), B({\mathbb C}^2 )]_{B({\mathbb C}^2 )}
\end{align*}
と定める.
$f_1, f_2 \in H$
を
\begin{align*}
f_1
=
\left[\begin{array}{ll}
1
\\
0
\end{array}\right],
\qquad
f_2
=
\left[\begin{array}{ll}
0
\\
1
\end{array}\right]
\end{align*}
とする.
さて,
\begin{align*}
u=\frac{f_1 +f_2}{{\sqrt 2}}
\end{align*}
として,
状態
$\rho = |u \rangle \langle u |$
$(\in {\frak S}^p(B({\mathbb C}^2)))$
を固定する.
ユニタリ作用素$U (\in B({\mathbb C}^2 ))$は次を満たすとする.
\begin{align*}
U ((\alpha_1 f_1 + \alpha_2 f_2))
=
\alpha_1 f_1
+
\alpha_2 {\sqrt{-1}}f_2
\end{align*}
因果作用素$\Phi: B({\mathbb C}^2 ) \to B({\mathbb C}^2 ) $
を
\begin{align*}
\Phi (F ) = U^* F U,
\qquad
(\forall F \in B({\mathbb C}^2)
)
\end{align*}
とする. すなわち,
\begin{align*}
B({\mathbb C}^2) \ni \Phi (F )= U^* F U \;\; {\longleftarrow \! \shortmid}\;\; F \in B({\mathbb C}^2)
\end{align*}
とする.
ここで, $B({\mathbb C}^2 )$内の二つの観測量
${\mathsf O}_f=(\{1,2\}, 2^{\{1,2\}}, F)$
と
${\mathsf O}_g=(\{1,2\}, 2^{\{1,2\}}, G)$
を次のように定める.
\begin{align*}
&
F(\{1\}) = |f_1 \rangle \langle f_1 | ,
\quad F(\{ 2 \}) = |f_2 \rangle \langle f_2 |
\end{align*}
と
\begin{align*}
&
G(\{1\}) = |g_1 \rangle \langle g_1 | ,
\quad G(\{ 2 \}) = |g_2 \rangle \langle g_2 |
\end{align*}
ここで,
\begin{align*}
&
g_1 = \frac{f_1 + f_2 }{\sqrt{2}},
\qquad
g_2 = \frac{f_1 - f_2 }{\sqrt{2}}
\end{align*}
11.6.3: ド・ブロイのパラドックスの$B({\mathbb C}^2)$版(干渉なし)
-
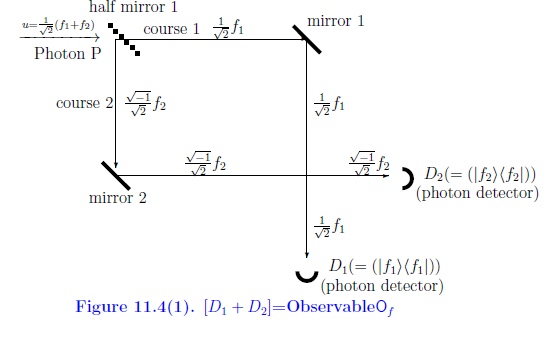
上図の気分をシュレーディンガー描像で説明しよう.
状態$u=\frac{1}{\sqrt{2}}( f_1+f_2 )$
(正確には,
$\rho=|u \rangle \langle u |$
)を持つ光子$P$がハーフミラー1に突入するとしよう.
| $(B_1):$ |
$f_1$部分はハーフミラー1を通過して経路1に沿って運動してミラー2で反射する.
それから,光子カウンター$D_1$に向かう.
|
| $(B_2):$ |
$f_2$はハーフミラー1で反射して,$\sqrt{-1}f_2$となって経路2に沿って運動してミラー1で反射する(位相が90度ずれるので$\sqrt{-1}$を掛けたが,これを気にすることはない).それから,光子カウンター$D_2$に向かう.
|
これをハイゼンベルグ描像で書けば,次の測定:
\begin{align}
{\mathsf M}_{B({\mathbb C}^2)} (\Phi {\mathsf O}_f, S_{[\rho]} )
\tag{11.21}
\end{align}
を得る.
このとき,
| $(C):$ |
測定
$
{\mathsf M}_{B({\mathbb C}^2)} (\Phi {\mathsf O}_f, S_{[\rho]} )
$
によって,$\left[\begin{array}{ll} \mbox{測定値 }1 \\ \mbox{測定値 }2 \end{array}\right]$
が得られる確率は,
\begin{align}
&
\left[\begin{array}{ll}
{\mbox{Tr}}(\rho \cdot \Phi F(\{1\}) )
\\
{\mbox{Tr}}(\rho \cdot \Phi F(\{2\}) )
\end{array}\right]
=
\left[\begin{array}{ll}
\langle Uu, F(\{1\})Uu \rangle
\\
\langle Uu, F(\{2\}) Uu \rangle
\end{array}\right]
=
\left[\begin{array}{ll}
| \langle Uu, f_1 \rangle|^2
\\
| \langle Uu, f_2 \rangle|^2
\end{array}\right]
=
\left[\begin{array}{ll}
\frac{1}{2}
\\
\frac{1}{2}
\end{array}\right]
\\
&
\tag{11.22}
\end{align}
で与えられる.
|
結局,光子カウンター$D_1$と$D_2$のいずれか一方が,半々の確率で,
カウントされることになる.
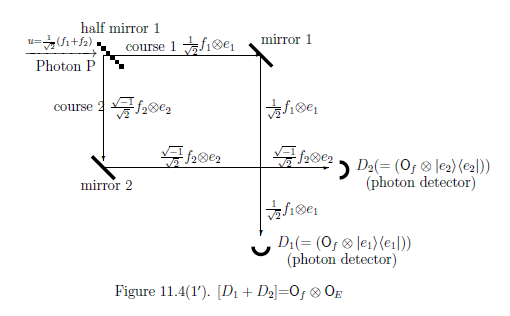
Remark 11.18 [Projection postulate]
時空と量子もつれに密接な関係があると仮定して、
図11.4(1)は次図のように書き直す。すなわち、
$e_1= \begin{bmatrix}
1
\\
0
\end{bmatrix}
$
and
$e_2= \begin{bmatrix}
0
\\
1
\end{bmatrix}
$
$( \in {\mathbb C}^2 )$,
$( \in {\mathbb C}^2 )$と置いて、
$B({\mathbb C}^2)$内の観測量${\mathsf O}_E=(\{1,2\},2^{\{1,2\}}, E)$
を$E( \{1 \})=|e_1 \rangle \langle e_1$、$E( \{1 \})=|e_1 \rangle \langle e_1$と定める。
上図(シュレーデインガー描像に依る)から、
\begin{align*}
u=\frac{1}{\sqrt 2}(f_1+f_2) \xrightarrow[\mbox{time evolution}]{}
\frac{1}{\sqrt 2}{f_1}{ \otimes e_1 }
+
\frac{{\sqrt{-1}}}{\sqrt 2}{f_2}{ \otimes e_2}
\end{align*}
を得る。
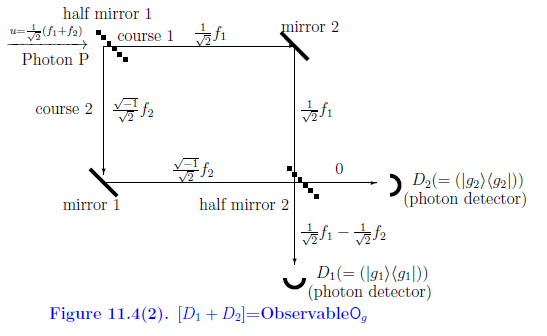
11.6.4: マッハ=ツェンダー干渉計(干渉あり)
次に,ハーフミラー2を付け加えた下図を想定する.
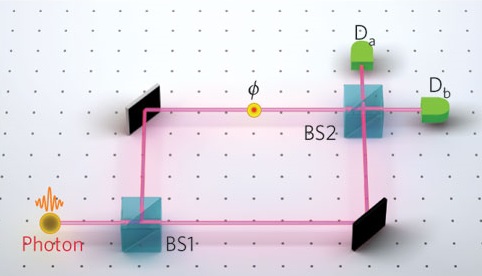
上図の気分をシュレーディンガー描像で説明しよう.
状態$u=\frac{1}{\sqrt{2}}( f_1+f_2 )$(正確には,
$\rho=|u \rangle \langle u |$
)を持つ光子$P$がハーフミラー1に突入するとしよう.
| $(D_1):$ |
$f_1$部分はハーフミラー1を通過して経路1に沿って運動してミラー2で反射する.
それから,ハーフミラー2を通過して光子カウンター$D_1$に向かう.
|
| $(D_2):$ |
$f_2$はハーフミラー1で反射して,$\sqrt{-1}f_2$となって経路2に沿って運動してミラー1で反射する(位相が90度ずれるので$\sqrt{-1}$を掛けたが,これを気にすることはない).それから,ハーフミラー2に反射して光子カウンター$D_1$に向かう.したがって,
離れ離れになった$f_1$と$f_2$は再会して合体して(すなわち,干渉して),光子カウンター$D_1$に向かう.
|
これをハイゼンベルグ描像で書けば,次の測定:
$
{\mathsf M}_{B({\mathbb C}^2)} (\Phi^2 {\mathsf O}_g, S_{[\rho]} )
$
を得る.
このとき,
| $(E):$ |
測定
$
{\mathsf M}_{B({\mathbb C}^2)} (\Phi^2 {\mathsf O}_g, S_{[\rho]} )
$
によって,$\left[\begin{array}{ll} \mbox{測定値 }1 \\ \mbox{ 測定値 }2 \end{array}\right]$
が得られる確率は
\begin{align}
\left[\begin{array}{ll}
{\mbox{Tr}}(\rho \cdot \Phi^2 G(\{1\}) )
\\
{\mbox{Tr}}(\rho \cdot \Phi^2 G(\{2\}) )
\end{array}\right]
=
\left[\begin{array}{ll}
\langle u, \Phi^2 G(\{1\})u \rangle
\\
\langle u, \Phi^2 G(\{2\}) u \rangle
\end{array}\right]
=&
\left[\begin{array}{ll}
| \langle u, UUg_1\rangle |^2
\\
| \langle u, UU g_2 \rangle|^2
\end{array}\right]
=
\left[\begin{array}{ll}
0
\\
1
\end{array}\right]
\\
&
\tag{11.23}
\end{align}
となる.
|
結局,光子カウンター$D_1$が
カウントされることになる.
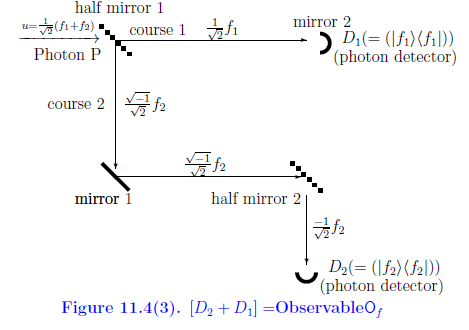
11.6.5: もう一つ付け加えると
次の図11.4(3)の状況を考えよう.
上図の気分をシュレーディンガー描像で説明しよう.
状態$u=\frac{1}{\sqrt{2}}( f_1+f_2 )$(正確には,
$\rho=|u \rangle \langle u |$
)を持つ光子$P$がハーフミラー1に突入するとしよう.
| $(F_1):$ |
$f_1$部分はハーフミラー1を通過して経路1に沿って運動して,
光子カウンター$D_1$に向かう.
|
| $(F_1):$ |
$f_2$はハーフミラー1で反射して,$\sqrt{-1}f_2$となって経路2に沿って運動してミラー1で反射する(位相が90度ずれるので$\sqrt{-1}$を掛けたが,これを気にすることはない).それから,ハーフミラー2に反射して光子カウンター$D_2$に向かう.
|
もちろん,これは
図11.7(1)の状況と等しい.
したがって,同じ測定
\begin{align}
{\mathsf M}_{B({\mathbb C}^2)} (\Phi^2 {\mathsf O}_f, S_{[\rho]} )
\tag{11.24}
\end{align}
を考えればよい.
したがって,(C)と同じだが,
| $(G):$ |
測定
$
{\mathsf M}_{B({\mathbb C}^2)} (\Phi^2 {\mathsf O}_f, S_{[\rho]} )
$
によって,$\left[\begin{array}{ll} \mbox{測定値 }1 \\ \mbox{測定値 }2 \end{array}\right]$
が得られる確率は,
\begin{align*}
\left[\begin{array}{ll}
{\mbox{Tr}}(\rho \cdot \Phi F(\{1\}) )
\\
{\mbox{Tr}}(\rho \cdot \Phi F(\{2\}) )
\end{array}\right]
=
\left[\begin{array}{ll}
\langle Uu, F(\{1\})Uu \rangle
\\
\langle Uu, F(\{2\}) Uu \rangle
\end{array}\right]
=
\left[\begin{array}{ll}
| \langle Uu, f_1 \rangle|^2
\\
| \langle Uu, f_2 \rangle|^2
\end{array}\right]
=
\left[\begin{array}{ll}
\frac{1}{2}
\\
\frac{1}{2}
\end{array}\right]
\end{align*}
で与えられる.
したがって,光子カウンター$D_1$が反応しなかったら,
確実に光子カウンター$D_2$が反応することが予期できる.
これは,光子を全く擾乱させずに測定できたことを意味する.
|
11.6.6: 結論
上述は「ウィーラーの遅延選択実験」と言われる有名なパラドックスで,
すなわち、
| $(\sharp):$ |
光子$P$が、"half-mirror 1"を通過して、「粒子」か「波」
が決定されてから、"half-mirror 2"を設置することを考えると、「粒子」ならば、"half-mirror 2"
を設置しても干渉するわけがない。 しかし、これでも干渉する(マッハ=ツェンダー干渉計)ということは、"half-mirror 2"を設置した
瞬間に、「粒子が波に逆戻り」したのだろうか?
|
というのが、ウィーラーの遅延選択実験である。
-
ウィーラーの説明を聞くと,遅延選択実験のパラドックスに納得してしまうかもしれない
しかし,これは,「ウィーラーの説明が量子言語でなされていない」からである.この節の量子言語による説明では,パラドックス的なことは現れない.
すなわち、量子言語の主張は、次のこと
だけである。
| $\quad$ |
$
\left\{\begin{array}{ll}
\mbox{
$\S$11.6.3 (Figure 11.4(1))
}: {\Phi} {\mathsf O}_f \quad & \xleftarrow[\mbox{ ハイゼンベルグ描像}]{\Phi} {\mathsf O}_f
\\
\mbox{
$\S$11.6.4 (Figure 11.4(2))
}:{\Phi^2} {\mathsf O}_g \quad & \xleftarrow[\mbox{ ハイゼンベルグ描像}]{\Phi^2} {\mathsf O}_g
\\
\mbox{
$\S$11.6.5 (Figure 11.4(3))
}:{\Phi^2} {\mathsf O}_g \quad & \xleftarrow[\mbox{ ハイゼンベルグ描像}]{\Phi^2} {\mathsf O}_f
\end{array}\right.
$
|
結局、
-
上の$(\sharp)$は、「盛り過ぎ」の説明である
教訓として
| $(H):$ |
パラドックス的文言があったら,それを量子言語で記述しようとすると、
記述できないことがしばしばある。
そうだとしたら、
それは「盛り過ぎ」の説明で、
すなわち、ウィトゲンシュタインの意味で、
という意味で、
パラドックスが解消されたことになる。
|
である,
| $\fbox{注釈11.3}$ |
言語的世界観の肝であるウィトゲンシュタインの有名な言葉:
語り得ぬことには、沈黙しなければならない
|
によって、「量子力学のパラドックス」を解消しようという試みは、
量子言語によってかなりの成功をしていると思う。
もちろん,超光速(非局所性)は,量子力学ではいつでも驚くべきパラドックスであって、これが量子言語で解消されることはないが、
他のパラドックスは、量子言語の記述により解消されると信じる。
.png)