${\mathbb C}^2$を二次元ヒルベルト空間とする.
すなわち,
${\mathbb C}^2$
$=$
$
\Big\{
\left[\begin{array}{ll}
z_1
\\
z_2
\\
\end{array}\right]
\;|
\;
z_1, z_2 \in {\mathbb C}
\Big\}$.
And put
\begin{align*}
e_1 =\left[\begin{array}{ll}
1
\\
0
\\
\end{array}\right],
\qquad
e_2 =\left[\begin{array}{ll}
0
\\
1
\\
\end{array}\right]
\end{align*}
$B({\mathbb C}^2)$
内の
観測量
${\mathsf O}_x=(\{-1, 1 \}, 2^{\{-1, 1 \}}, F_x )$
を次のように定める.
\begin{align*}
F_x(\{ 1 \} ) = \frac{1}{2}
\left[\begin{array}{ll}
1 & 1
\\
1 & 1
\\
\end{array}\right],
\quad
F_x(\{ -1 \} ) = \frac{1}{2}
\left[\begin{array}{ll}
1 & -1
\\
-1 & 1
\\
\end{array}\right],
\end{align*}
次は,明らか.
\begin{align*}
&
F_x(\{ 1 \} )e_1 = \frac{1}{2}(e_1 + e_2 ),
\quad
F_x(\{ 1 \} )e_2 = \frac{1}{2}(e_1 + e_2 )
\\
&
F_x(\{ -1 \} )e_1 = \frac{1}{2}(e_1 - e_2 ),
\quad
F_x(\{ -1 \} )e_2 = \frac{1}{2}(-e_1 + e_2 )
\end{align*}
また,$B({\mathbb C}^2)$内の存在観測量
${\mathsf O}_E=(\{ 1 \}, 2^{\{ 1 \}}, F_E )$
をいつものように,次で定める.
\begin{align*}
F_E(\{ 1 \} ) =
\left[\begin{array}{ll}
1 & 0
\\
0 & 1
\\
\end{array}\right]
\qquad
F_E(\emptyset ) =
\left[\begin{array}{ll}
0 & 0
\\
0 & 0
\\
\end{array}\right]
\end{align*}
$H$をヒルベルト空間とする.
たとえば,
\begin{align*}
H=L^2({\mathbb R}_q )
=
\Big\{ u: {\mathbb R}_q \to {\mathbb C } \;\Big|\;
\Big[\int_{{\mathbb R}_q } |u (q ) |^2 dq\Big]^{1/2} < \infty \Big\}
\end{align*}
とする.
$B(H)$内の観測量
${\mathsf O}=(X, {\mathcal F}, F)$を考える.
たとえば,$H=L^2({\mathbb R}_q )$,
$X={\mathbb R}$,
${\mathcal F}={\mathcal B}_{\mathbb R}$
として,
\begin{align*}
[F(\Xi)] (q)
=\begin{cases}
1 \qquad & (q \in \Xi \in {\mathcal F} )
\\
0 \qquad & (q \notin \Xi \in {\mathcal F})
\end{cases}
\end{align*}
とする.
$u_1, u_2 \in H$を正規直交系とする.
すなわち,
\begin{align*}
||u_1 ||_H = ||u_2 ||_{H} = 1,
\quad
\langle u_1, u_2 \rangle_H = 0
\end{align*}
とする.
11.7.2: 干渉あり
ここに,
第三項(干渉項)
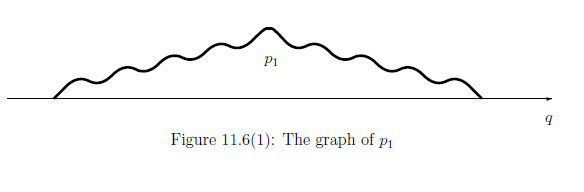
に注意せよ.さらに,次のように確率密度関数$\rho_1$を定める
この節は、以下の論文からの抜粋である。
$(\sharp):$
S. Ishikawa,
double-slit quantum eraser experimentsとHardy's paradox in quantum linguistic interpretation,
arxiv:1407.5143[quantum-ph],( 2014)
11.7.1: テンソルヒルベルト空間
テンソルヒルベルト空間${\mathbb C}^2 \otimes H $
を考える.
さて,
$\psi \in {\mathbb C}^2 \otimes H $
$($
を次のように定める.
\begin{align*}
\psi =
\alpha_1 e_1 \otimes u_1 + \alpha_2 e_2 \otimes u_2
\end{align*}
ここに,$\alpha_i \in {\mathbb C}$,
$| \alpha_1|^2 + |\alpha_2|^2=1$.
次の測定を考える:
\begin{align}
{\mathsf M}_{B({\mathbb C}^2 \otimes H )}
({\mathsf O}_x \otimes {\mathsf O} , S_{[| \psi \rangle \langle \psi |]} )
\tag{11.27}
\end{align}
言語ルール1(測定)より
\begin{align*}
&
\langle
\psi,
(F_x(\{ 1 \}) \otimes F(\Xi) )
\psi
\rangle
\\
=
&
\langle
\alpha_1 e_1 \otimes u_1 + \alpha_2 e_2 \otimes u_2,
(F_x(\{ 1 \} \otimes F(\Xi) ))
(
\alpha_1 e_1 \otimes u_1 + \alpha_2 e_2 \otimes u_2
)
\rangle
\\
=
&
\frac{1}{2}
\langle
\alpha_1 e_1 \otimes u_1 + \alpha_2 e_2 \otimes u_2,
\alpha_1 (e_1+e_2) \otimes F(\Xi) u_1 + \alpha_2 (e_1+ e_2) \otimes F(\Xi) u_2
\rangle
\\
=
&
\frac{1}{2}
\Big(
|\alpha_1|^2
\langle
u_1 ,
F(\Xi)u_1
\rangle
+
|\alpha_2|^2
\langle
u_2 ,
F(\Xi)u_2
\rangle
+
\overline{\alpha}_1\alpha_2
\langle
u_1 ,
F(\Xi)u_2
\rangle
+
{\alpha}_1 \overline{\alpha}_2
\langle
u_2 ,
F(\Xi)u_1
\rangle
\Big)
\\
=
&
\frac{1}{2}
\Big(
|\alpha_1|^2
\langle
u_1 ,
F(\Xi)u_1
\rangle
+
|\alpha_2|^2
\langle
u_2 ,
F(\Xi)u_2
\rangle
+
2
\mbox{[Real part]}
(
\overline{\alpha}_1\alpha_2
\langle
u_1 ,
F(\Xi)u_2
\rangle
)
\Big)
\\
\end{align*}
$(A_1):$
測定値
$(1, x ) (\in \{-1,1\} \times X )$
が,
$
\{1\} \times \Xi $
に属する確率は,次のように計算できる:
また,次を得る.
| $(A_2):$ | 測定値 $(-1, x ) (\in \{-1,1\} \times X )$ が, $ \{1\} \times \Xi $ に属する確率は,次のように計算できる: |
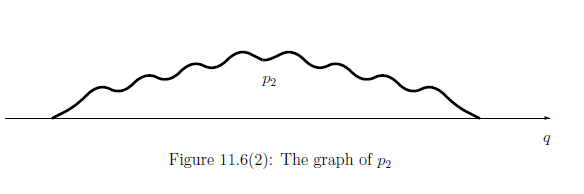
ここに, 第三項(干渉項) に注意せよ.さらに,次のように確率密度関数$\rho_2$を定める
\begin{align*} =: & \int_{\Xi} \rho_2 (q ) dq \qquad (\forall \Xi \in {\mathcal F} ) \end{align*}次の測定測定: \begin{align} {\mathsf M}_{B({\mathbb C}^2 \otimes H )} ({\mathsf O}_E \otimes {\mathsf O} , S_{[| \psi \rangle \langle \psi |]} ) \tag{11.29} \end{align} を考える. 言語ルール1(測定)から,
| $(A_3):$ | 測定値 $(1, x ) (\in \{1\} \times X )$ が $ \{1\} \times \Xi $ に属する確率は |
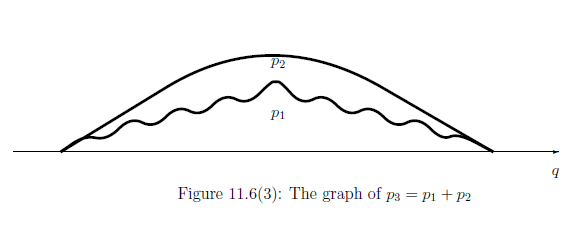
ここに, 第三項(干渉項) が無いことに注意せよ.さらに,次のように確率密度関数$\rho_3$を定める
\begin{align*} =: & \int_{\Xi} \rho_3 (q ) dq \qquad (\forall \Xi \in {\mathcal F} ) \end{align*}注意11.17
上で \begin{align*} \overset{{\mbox{(A$_3$)}}}{\underset{\mbox{干渉項なし}}{\fbox{$\quad \rho_3 \quad$}}} = \overset{{\mbox{(A$_1$)+(A$_2$)}}}{\underset{\mbox{干渉項が相殺}}{\fbox{$\quad \rho_1$+$\rho_2 \quad$}}} \end{align*} に注意せよ.