12.2 Double-slit experiment

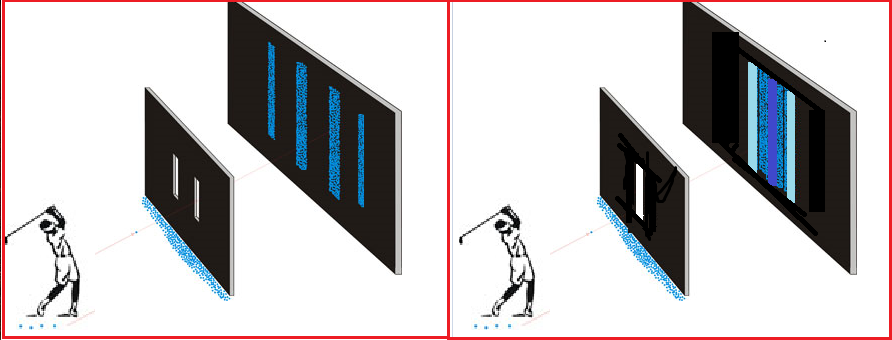
この節は、次の論文からの抜粋である：

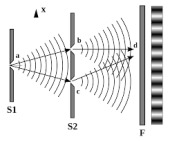
$(\sharp):$ S. Ishikawa, double-slit quantum eraser experiments and Hardy's paradox in quantum linguistic interpretation, arxiv:1407.5143[quantum-ph],( 2014)

12.2.1. 干渉あり
各$t \in T=[0, \infty )$　に対して, 量子基本構造を次のようにする： \begin{align*} [{\mathcal C}(H_t) \subseteq B(H_t) \subseteq B(H_t)] , \end{align*} ここに $H_t=L^2({\mathbb R}^2 )$ $(\forall t \in T)$.

初期波動関数$u_0 \in H_0 = L^2({\mathbb R}^2 )$ ($k_0>0$, small $\sigma > 0$) を以下に定める：

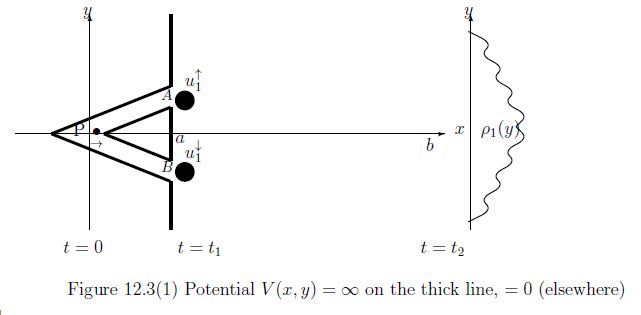
\begin{align*} u_0(x,y) \approx \psi_x(x,0) \psi_y (y,0) = \frac{1}{\sqrt{\pi^{1/2}\sigma }} \exp \Big(ik_0 x -\frac{x^2}{2\sigma ^2}\Big) \cdot \frac{1}{\sqrt{\pi^{1/2}\sigma }} \exp \Big(-\frac{y^2}{2\sigma^2}\Big), \end{align*} ここで、 平均運動量$(p^0_1,p^0_2)$は次のように計算できる： \begin{align*} (p^0_1,p^0_2)= \Big( \int_{\mathbb R} {\overline \psi}_x(x,0) \cdot \frac{\hbar \partial \psi_x(x,0)}{i \partial x} dx, \int_{\mathbb R} {\overline \psi}_y(y,0) \cdot \frac{\hbar \partial \psi_y(y,0)}{i \partial y} dy \Big) = (\hbar k_0, 0 ). \end{align*}

以下に、次図を説明しよう。
Picture 12.9 ${\mathsf M}_{B(H_0)} (\Phi_{0,t_2} {\mathsf O}_2=( {\mathbb R}, {\mathcal B}_{\mathbb R}, \Phi_{0,t_2} F_2), S_{[|u_0\rangle \langle u_0|]} )$
次のシュレーディンガー方程式を想定する： \begin{align*} i \hbar \frac{\partial}{\partial t } u_t(x,y) = {\mathcal H} u_t(x,y), \qquad {\mathcal H} = -\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2} - \frac{\hbar^2}{2m}\frac{\partial^2}{\partial y^2} + V(x,y) \end{align*}

したがって、$0 < s < t < \infty $として、 次の因果関係 $ \{ \Phi_{s,t}: B(H_{t}) \to B(H_s) \}_{0 < s < t < \infty } $ を得る。 ここで、

\begin{align*} & \Phi_{s,t} A =e^{ \frac{{\mathcal H} (t-s) }{i \hbar } } A e^{- \frac{{\mathcal H} (t-s) }{i \hbar } } \qquad (\forall A \in B(H_{t})=B(L^2({\mathbb R}^2 ) ) ) \end{align*} すなわち, Picture 12.9において、$(\Phi_{0,t_1})_* (u_0)= u_1^\uparrow + u_1^\downarrow$。

ここで、 ${\mathsf O}_2=( {\mathbb R}, {\mathcal B}_{\mathbb R}, F_2)$を$B(L^2({\mathbb R}^2 )$内の $y$方向に位置観測量とする。　すなわち、

\begin{align*} [F(\Xi )](x,y) = \chi_{\Xi}( y ) = \begin{cases} 1 \qquad & ( x,y ) \in {\mathbb R} \times \Xi \\ \\ 0 \qquad & ( x,y ) \in {\mathbb R} \times {\mathbb R} \setminus \Xi \end{cases} \end{align*}

したがって、測定 ${\mathsf M}_{B(H_0)} (\Phi_{0,t_2} {\mathsf O}_2=( {\mathbb R}, {\mathcal B}_{\mathbb R}, \Phi_{0,t_2} F_2), S_{[|u_0\rangle \langle u_0|]} )$ を得る。 言語ルール1( measurement: $\S$2.7) によれば、次が言える：

$(A):$ ${\mathsf M}_{B(H_0)} (\Phi_{0,t_2} {\mathsf O}, S_{|u_0\rangle \langle u_0|} )$ によって得られた測定値$a \in {\mathbb R} $ が$( - \infty , y ]$に属する確率は次で与えられる： $$ \langle u_0 , (\Phi_{0,t_2} F( ( - \infty , y ] )) u_0 \rangle = \int_{- \infty }^y \rho_1 ( y) dy $$

$\fbox{Note 12.3}$ もうすこし正確に言うと、以下のようになる。 $\Delta$, $\epsilon$ を小さい正数とする。 各正数$k \in {\mathbb Z}=\{k \; | \; k=0, \pm 1, \pm 2, \pm 3, ,,,,\}$に対して, 長方形$D_k$を次のように定める。 \begin{align*} & D_0=\{ (x,y) \in {\mathbb R}^2 \;|\; x < b \}, \\ & D_k = \{ (x,y) \in {\mathbb R}^2 \;|\; b \le x, (k-1) \Delta < y \le k \Delta \}, \quad k=1,2,3,... \\ & D_k = \{ (x,y) \in {\mathbb R}^2 \;|\; b \le x, k \Delta < y \le (k+1) \Delta \}, \quad k=-1,-2,-3,... \end{align*} ここで、$B(L^2({\mathbb R}^2 ))$内の観測量${\mathsf O}_2^\Delta =( {\mathbb Z} , 2^{\mathbb Z}, F_2^\Delta )$を次のように定める： $$ [F(\{k\})](x,y)= 1 \;\; ((x,y) \in D_k), \quad = 0 \;\; ((x,y) \in {\mathbb R}^2 \setminus D_k) \qquad ( k \in {\mathbb Z} ) $$ よって、次のように考えればよい。
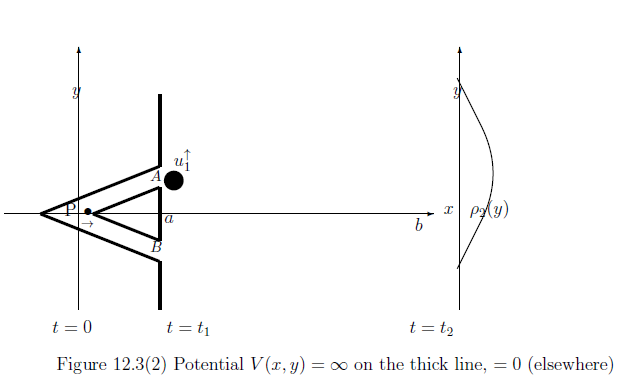
$\bullet$ 各時刻$t_n = t_2 + n \epsilon (n=0,1,2,...)$に対して, 射影観測量 ${\mathsf O}_2^\Delta$を 射影仮説11.7の意味で測定する。


12.2.2. Which-way path experiment (どっちのスリットを通ったか？) 次の図を説明しよう。
Picture 12.10 Which-way path experiment:$\;\;$ 測定${\mathsf M}_{B(L^2({\mathbb R}^2 ))} ( \Phi_{0, t_1 } ( \Psi( {\mathsf O}_G \otimes \Phi_{t_1, t_2 } {\mathsf O}_2)), S_{[| u_0 \rangle \langle u_0 |]} )$の測定値が $\{ \uparrow \} \times ( - \infty , y ]$に属した場合

$B(L^2( {\mathbb R}^2 ))$内の 射影観測量 ${\mathsf O}_1=( \{ \uparrow , \downarrow \}, 2^{ \{ \uparrow , \downarrow \}}, F_1 )$ を次のように定める：

\begin{align*} & [F_1 ( \{ \uparrow \} )](x,y ) = \begin{cases} 1 \qquad & y \ge 0 \\ 0 & y < 0 \end{cases} \\ & [F_1 ( \{ \downarrow \} )](x,y ) = 1- [F_1 ( \{ \uparrow \} )](x,y ) \end{align*}

射影仮説11.7 ( in Section 11.2)を使うために、 完全正規直交系$\{ e_1, e_2 \}$ $( \in {\mathbb C}^2 )$を固定する。 前共役作用素 $\Psi_*: Tr(L^2( {\mathbb R}^2 )) \to Tr({\mathbb C}^2 \otimes L^2( {\mathbb R}^2 ))$ を次のように定める：

$$ \Psi_* ( |u \rangle \langle u | ) = |(e_1 \otimes F_1 (\{ \uparrow \} ) u ) + (e_2 \otimes F_1 (\{ \downarrow \} ) u ) \rangle \langle (e_1 \otimes F_1 (\{ \uparrow \} ) u ) + (e_2 \otimes F_1 (\{ \downarrow \} ) u )| $$

よって、　因果作用素 $\Psi: B ({\mathbb C}^2 \otimes L^2( {\mathbb R}^2 )) \to B(L^2( {\mathbb R}^2 ))$ を $\Psi= (\Psi_* )^*$で得る。 $B({\mathbb C}^2)$内の観測量 ${\mathsf O}_G =( \{ \uparrow , \downarrow \}, 2^{ \{ \uparrow , \downarrow \}}, G )$ を次のように定める：

$$ G( \{ \uparrow \} )= | e_1 \rangle \langle e_1 |, \qquad G( \{ \downarrow \} )= | e_2 \rangle \langle e_2 | $$

よって、テンソル観測量 ${\mathsf O}_G \otimes \Phi_{t_1, t_2 } {\mathsf O}_2$ (in $B( {\mathbb C}^2 \otimes L^2({\mathbb R}^2 ))$) を得て、 測定 ${\mathsf M}_{B(L^2({\mathbb R}^2 ))} ( \Phi_{0, t_1 } ( \Psi( {\mathsf O}_G \otimes \Phi_{t_1, t_2 } {\mathsf O}_2)), S_{[| u_0 \rangle \langle u_0 |]} )$も得る。 言語ルール1 ( measurement: $\S$2.7) によって、次が言える：

$(B):$ 測定 ${\mathsf M}_{B(L^2({\mathbb R}^2 ))} ( \Phi_{0, t_1 } ( \Psi( {\mathsf O}_G \otimes \Phi_{t_1, t_2 } {\mathsf O}_2)), S_{[| u_0 \rangle \langle u_0 |]} )$ によって得られた測定値 $( \lambda , y ) \in \{\uparrow, \downarrow \} \times {\mathbb R} $ が $\{ \uparrow \} \times ( - \infty , y ]$に属する確率は 次のようになる： $$ \langle u_1^\uparrow , (\Phi_{t_1,t_2} F_2( ( - \infty , y ] )) u_l^\uparrow \rangle = \frac{1}{2} \int_{- \infty }^y \rho_2 ( y) dy $$

$\fbox{Note 12.4}$ 厳密に言えば, 「粒子$P$がホール$A$を通った」 という命題は量子言語では記述できないが、上の議論をもうすこし正確に言うならば、 次の手続き (i) and (ii)を考えればよい：
(i): 時刻$t_1$で, 射影観測量${\mathsf O}_1$を射影公準11.7の意味で 測定する
(ii): 各$t_n = t_2 + n \epsilon (n=0,1,2,...)$に対して, 射影観測量${\mathsf O}_2^\Delta$を射影公準11.7の意味で 測定する