本書では,
「統計学=動的システム理論」
─
微分方程式と確率論という数学の応用的手法
という意味では同じもの
─
と考えるが,
「推定問題」は統計学,
「制御問題」は動的システム理論
と仕切りがされていると考えるのが,普通かもしれない.
しかし,
この2つは
同類の問題である.
以下にこのことを説明して,
「統計学=動的システム理論」を再確認する.
13.1.1:推定問題(統計学)
問題13.1[推定問題と回帰分析]
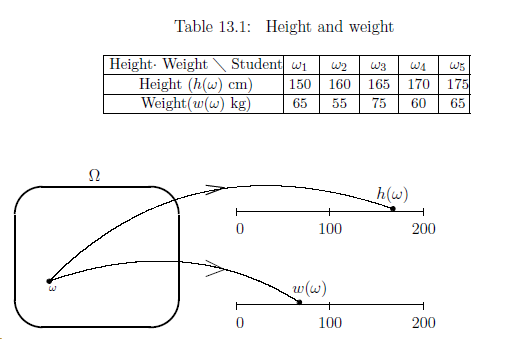
$\Omega $
${{=}}$
$\{ \omega_1 , \omega_2 ,\ldots , \omega_{N} \}$
をある高校の学生の集合とする.
身長関数$h : \Omega \to [{}100, 200{}]$
と
体重関数$w : \Omega \to [{}30, 110{}]$
を次のように定義する:
\begin{align}
\begin{cases}
h (\omega_n{}) =
\text{ "学生$\omega_n$の身長" }
\\
w (\omega_n{}) =
\text{ "学生$\omega_n$の体重" }
\end{cases}
\quad
\qquad
(n= 1,2,3,..., N{})
\tag{13.1)}
\end{align}
簡単のため,
$N=5$として,
たとえば,表13.1を仮定する.
次を仮定する:
| $(a_1):$ |
この高校では健康診断を実施しているので,
校長は,
表13.1のデータ
─
すべての学生の身長と体重
─
を正確に把握している.
|

更に,次の$(a_2)$を仮定する:
| $(a_2):$ |
ある日,この高校のある学生が川で溺れている少年を助けた.
しかし,その学生は名前も名乗らずにその場を立ち去った.
わかっていることは,
| $(ii):$ |
その学生の身長と体重はそれぞれ約165 cm
と約65 kgである.
|
|
ここで次の問題を考える:
| $(b):$ |
上の情報$(a_1)$と$(a_2)$から,
校長はその学生が誰かを如何に推定するか?
|
この推定問題(b)は回帰分析を使う典型的な例で,
測定理論の言葉によって解答13.5で答える.
13.1.2;制御問題(動的システム理論)
状態方程式
(一階連立微分方程式)
に,
測定方程式
$g: {\mathbb R}^3 \to {\mathbb R}$を加えて,
以下のように,動的システム理論(13.2)
を考える.
すなわち,
\begin{align}
\fbox
{
動的システム理論
}
=
\begin{cases}
{\rm{(i)}}:
\underset{
(初期条件 \omega(0)=\alpha)}{\frac{d \omega (t)}{dt} =
v(\omega(t), t{}, e_1(t), \beta)}
\; & \cdots \text{( 状態方程式)}
\\
\\
{\rm{(ii)}}:
x(t) = g(\omega(t), t{}, e_2 (t) ) \;
& \cdots
\mbox{(
測定方程式)}
\end{cases}
\tag{13.2}
\end{align}
とする.
ここに,
$\alpha, \beta $
はパラメータ,
$e_1 (t)$はノイズ,
$e_2 (t)$は測定誤差
とする.
以下の例は,
動的システム理論における
制御問題の中で,
最も簡単なものである.
問題13.2[制御問題と回帰分析]
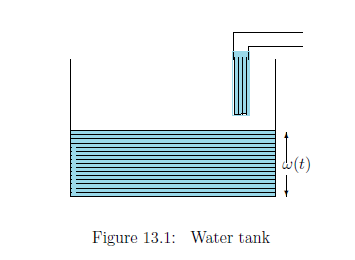
図7.1のように直方体の水槽に水を入れることを考える.
時刻$t$での水面の高さを関数 $\omega(t)$で表す.
流入速度を$\beta$として,
時刻$0$での初期水位を$\alpha$とする.
水位$\omega(t)$は次の状態方程式を満たす
(ここで,ノイズ$e_1(t)=0$とした).
\begin{align*}
\frac{d}{dt} \omega(t)
=
\beta
\cdots \text{(状態方程式) }
\end{align*}
$\omega (0)=\alpha$として,これを解けば,
\begin{align}
\omega(t) = \alpha + \beta t
\tag{13.3}
\end{align}
ここに,
$\alpha$
と
$\beta$
は
未知の固定されたパラメータと考える.
実際の測定値は誤差を含むので,測定方程式は次のようになる:
\begin{align*}
x(t) = \alpha + \beta t + e_2(t)
\cdots \mbox{(測定方程式) }
\end{align*}
ここに$e_2(t)$は測定誤差である.
次を仮定する:
\begin{align}
x(1)=1.9, \quad x(2)=3.0, \quad x(3)=4.7.
\tag{13.4}
\end{align}
この(13.4)を、以下のように二つの解釈(制御と推定)をする。
ここで次の制御問題を考える
(答えは測定理論の言葉で解答13.6(13.2節)で述べる):
| $(c_1):$ |
[制御問題]:
時刻$t=1,2,3$での
水位の目標測定データとして,次の
\begin{align*}
x(1)=1.9, \quad x(2)=3.0, \quad x(3)=4.7
\label{1data}
\end{align*}
を考えたい.
この目標測定データ
を得られるように
$\alpha$
と
$\beta$
を設定せよ.
|
である.
別の見方も重要で,この
$({\rm c}_1)$は次の推定問題$({\rm c}_2)$と同値である.
| $(c_2):$ |
[推定問題]:
時刻$t=1,2,3$での
水位の測定データが
\begin{align*}
x(1)=1.9, \quad x(2)=3.0, \quad x(3)=4.7
\end{align*}
が得られたとする.
このとき,
$\alpha$
と
$\beta$
を推定せよ.
|
ここで,
実質的には
(すなわち,測定理論のテクニカルな面としては),「(${\rm c}_1$)=(${\rm c}_2$)」なので,
| $(d):$ |
推定問題と制御問題は
同類の問題であり,
測定の逆問題である
|
ことに注意してもらいたい.
注意13.3 [動的システム理論についての注意]
(13.2)式に関して、以下に注意しよう:
| $(\sharp):$ |
ノイズ$e_1 (t)$
と測定誤差
$e_2 (t)$
は同じ数学構造
(確率過程)
を持つ.
|
これは動的システム理論(13.2)式
のウィーク・ポイントと考える。
異なる概念
(
ノイズ
と測定誤差
)
ならば、異なる数学構造で定式化された方が好ましい
と考えるからである。
ノイズ
と測定誤差
は混乱しやすいが、
量子言語においては
数学構造が異なるので、混乱を避けることができる。