木半順序集合を親写像表現
$(T{{=}} \{ t_0,t_1,$
$\ldots,$
$ t_N\} , \pi:
T \setminus \{ t_0 \} \to T)$
で表す.
因果観測量列
$[{}\{ {\mathsf O}_t \}_{ t \in T} ,
\{ \Phi_{\pi(t), t }{}: $
$L^\infty({\Omega}_{t}{})\to L^\infty({\Omega }_{\pi(t)}{}) \}_{ t \in T\setminus \{t_0\} }$
$]$の
実現因果観測量を
$\widehat{\mathsf O}_{T{}}$
${{=}} (
{{{\times}}}_{t \in T} X_t, $
${\boxtimes_{t \in T} {\cal F}_t}, $
$
{\widehat F}_{t_0})$
として,
測定
\begin{align*}
{\mathsf M}_{L^\infty (\Omega_{t_0})} (\widehat{\mathsf O}_{T{}} {{=}} (
{{{\times}}}_{t \in T} X_t, {\boxtimes_{t \in T} {\cal F}_t},
{\widehat F}_{t_0}), S_{[\ast]}{})
\qquad
\end{align*}
を考える.
この測定
${\mathsf M}_{L^\infty(\Omega_{t_0}{})}(\widehat{\mathsf O}_{T{}}, S_{[*]})$
により得られた測定値が
${\widehat \Xi}
\;(\in
{\boxtimes_{t \in T} {\cal F}_t}
)$
に属したとする.
このとき,
フィッシャーの最尤法(定理5.6)により,
次が推定できる:
\begin{align*}
[{}\ast{}]
=
{\omega_{t_0}}
\end{align*}
ここで,${\omega_{t_0}} \;(\in \Omega_{t_0})$
は
\begin{align*}
[\widehat F_{t_0} (
{\widehat \Xi}
)](\omega_{t_0}) =
\max_{\omega \in \Omega_{t_0}} [\widehat F_{t_0} (
{\widehat \Xi}
){}](\omega)
\end{align*}
によって定まる.
したがって、
一言で言えば、
\begin{align}
\textcolor{magenta}{\fbox{回帰分析}}
=
&
\textcolor{blue}{ \underset{(推定法)}{\fbox{フィッシャーの最尤法}} + \fbox{実現因果観測量}
}
\end{align}
である。
問題13.1
を測定理論の言葉
(すなわち,回帰分析(定理13.4))で答えよう.
木半順序集合を親写像表現
$(T{{=}} \{ 0,1,2\} , \pi:
T \setminus \{ 0 \} \to T)$
で表して,
$\pi(1)=\pi(2)=0$
とする.
状態空間を
$\Omega_0
=\{\omega_1, \omega_2,\ldots,\omega_5\}$,
$\Omega_1 = 区間
[100,200]$,
$\Omega_2 = 区間[30,110]$とおく.
もちろん,同一視:
\begin{align*}
\omega_n
・・・
\text{
「少年を助けたのが学生$\omega_n$である」
}
という状態
\quad
(n=1,2,...,5)
\end{align*}
を考える.
各
$t \;(\in \{ 1,2 \})$に対して,
決定的因果写像
$\phi_{0,t}{}: \Omega_0 \to \Omega_t $
を
$\phi_{0,1}=h$(身長関数),
$\phi_{0,2}=w$(体重関数)
と定める.
よって,
各
$t \;(\in \{ 1,2\})$に対して,
決定的因果作用素
$\Phi_{0,t}{}: L^\infty(\Omega_t) \to L^\infty(\Omega_0{}) $
は
次のように
定まる:
\begin{align*}
[\Phi_{0,t} f_t] (\omega)
= f_t (\phi_{0,t} (\omega){})
\qquad
(\forall \omega \in \Omega_0, \forall f_t \in L^\infty(\Omega_t))
\end{align*}
$t=1,2$
として,標準偏差$\sigma_t >0$を持つ
$C (\Omega_t)$内の{\it 正規観測量}
${\mathsf O}_{G_{\sigma_t}} =
({\mathbb R}, {\cal B}_{\mathbb R}, G_{\sigma_t})$,
すなわち,
\begin{align*}
[G_{\sigma_t}(\Xi)] (\omega) = \frac{1}{\sqrt{2 \pi \sigma_t^2}}
\int_{\Xi} e^{- \frac{(x - \omega)^2}{2 \sigma_t^2}} dx
\quad (\forall \Xi \in {\cal B}_{\mathbb R}, \forall \omega \in
\Omega_t
)
\end{align*}
十分に大きな自然数$N$に対して,区間
$\Xi_1, \Xi_2 \subset {\mathbb R}$
を,
${\mathsf M}_{L^\infty (\Omega_0)} (\widehat{\mathsf O}_{T{}},
S_{[\ast]}{})$により得られた測定値
は
(165,65) $ (\in {\mathbb R}^2)$
であるから,
測定値は
$\Xi_1 \times \Xi_2$
に属す.
ここで,
定理13.4[回帰分析]
(または,
フィッシャーの最尤法(定理5.6))
より,
問題
は,
よって,少年を助けたのは,
学生$\omega_4$と推定される.
問題13.2
では,離散時間
$T=\{0,1,2,3\}$
が
直列構造を持つと考えるのが自然で,
親写像$\pi :T\setminus\{0\} \to T$
を$\pi ( t ) = t-1$
$\;(t=1,2,3)$と定める.
4つの状態空間を,
たとえば,
$\Omega_0
= [0,\; 1]
\times [0,\; 2]
$,
$\Omega_1 =[0,\; 4] \times [0,\; 2]$,
$\Omega_2 = [0,,\; 6] \times [0,\; 2]$,
$\Omega_3 = [0, \; 8] \times [0,\; 2]$
更に,
$\sigma>0$を標準偏差として,
各
$t=1,2,3$に対して,
$L^\infty (\Omega_t)$内の
正規観測量
${\mathsf O}_{t} {{=}} ({\mathbb R}, {\cal B}_{\mathbb R}, G_{\sigma})$
を次のように定義する:
\begin{align*}
[G_{\sigma}(\Xi)] (\omega) = \frac{1}{\sqrt{2 \pi \sigma^2}}
\int_{\Xi} e^{- \frac{(x - \omega)^2}{2 \sigma^2}} dx
\quad (\forall \Xi \in {\cal B}_{\mathbb R}, \forall \omega \in \Omega_t
{{=}}
[{}0, \; 2t+2{}])
\end{align*}
よって,
決定的因果観測量列
$[ \{{\mathsf O}_{t}\}_{t=1,2,3}
,
\{\Phi_{\pi(t),t}{}: L^\infty(\Omega_{t}) \to L^\infty(\Omega_{\pi(t)}
)
\}_{t \in \{1,2,3\}}
]$
を得る.
このとき,
${L^\infty(\Omega_0{})}$内の
実現因果観測量
$\widehat{\mathsf O}_{T{}}$
${{=}}$
$({\mathbb R}^3, {\cal F}_{{\mathbb R}^3}, {\widehat F}_0)$
は,定理14.5より,
次のように定まる:
\begin{align*}
&
[{\widehat F}_0(\Xi_1 \times \Xi_2 \times \Xi_3{})]
(\omega_0)
=
\big[
\Phi_{0,1}
\big(G_{\sigma} ({\Xi_1})
\Phi_{1,2} (G_{\sigma} ({\Xi_2})
\Phi_{2,3} (G_{\sigma} ({\Xi_3})
))
\big)
\big]
(\omega_0)
\\
=
&
[\Phi_{0,1} G_{\sigma} ({\Xi_1})] (\omega_0)
\cdot
[\Phi_{0,2} G_{\sigma}({\Xi_2})] (\omega_0)
\cdot
[\Phi_{0,3} G_{\sigma}({\Xi_3})] (\omega_0)
\\
=
&
[G_{\sigma} ({\Xi_1})] (\phi_{0,1}(\omega_0){})
\cdot
[G_{\sigma} ({\Xi_2})] (\phi_{0,2}(\omega_0){})
\cdot
[G_{\sigma}({\Xi_3})] (\phi_{0,3}(\omega_0){})
\\
&
\qquad \qquad
(\forall \Xi_1, \Xi_2, \Xi_3 \in {\cal B}_{\mathbb R},
\;
\forall \omega_0 =(\alpha, \beta{}) \in \Omega_0
= [0, \; 1] \times [0, \; 2]{})
\end{align*}
さて,
問題13.2
(制御問題)は,
${\mathsf M}_{L^\infty (\Omega_0)} ($
$\widehat{\mathsf O}_{T{}}, $
$S_{[\ast]}{})$
によって,
測定値:
\begin{align*}
(1.9, \; 3.0, \; 4.7) \; (\in {\mathbb R}^3)
\end{align*}
よって,
目標測定値
$(1.9, \; 3.0, \; 4.7)$
を得るための,
$(\alpha, \beta)$
の制御状態$(0.4, \; 1.4)$
を得る.
以上であるが,
7.1.2節の
(d)で述べた
「制御問題$(c_1)$
と
推定問題$(c_2)$の
実質的同値性」
を再度確認してもらいたい.
念のために、確認すると、
である。
したがって、
統計学(推定が主)
と
動的システム理論(制御が主)
は本質的には同じと考える。
前章の結果
(すなわち,
言語ルール2(因果関係)
とフィッシャーの最尤法(定理5.6)
から
直ちに次を得る:
解答 13.5[問題13.1(推定問題)から続く)回帰分析]
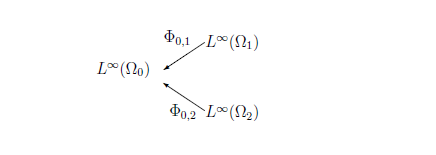
を考えて,
決定的因果観測量列
$[ \{{\mathsf O}_{G_{\sigma_t}}\}_{t=1,2}
,
\{
\Phi_{0, t}
:
L^\infty(\Omega_t) \to L^\infty(\Omega_0)\}_{t=1,2}
]$
を得る.
このとき,
${L^\infty(\Omega_0{})}$
内の
実現因果
観測量
$\widehat{\mathsf O}_{T{}}$
${{=}}$
$({\mathbb R}^2, {\cal F}_{{\mathbb R}^2}, {\widehat F}_0)$
を
次のように得る:
\begin{align*}
[{\widehat F}_0(\Xi_1 \times \Xi_2 {})]
(\omega)
&=
[\Phi_{0,1} G_{\sigma_1} ] (\omega)
\cdot
[\Phi_{0,2} G_{\sigma_2}] (\omega)
\\
&=
[G_{\sigma_1} ({\Xi_1})] (\phi_{0,1}(\omega){})
\cdot
[G_{\sigma_2} ({\Xi_2})] (\phi_{0,2}(\omega){})
\\
&
\qquad \qquad
(\forall \Xi_1, \Xi_2 \in
{\cal B}_{\mathbb R}
,
\;
\forall \omega \in \Omega_0
=
\{\omega_1, \omega_2,\ldots,\omega_5\}
)
\end{align*}
という問題に帰着される.
$N$は十分に大きいから,
\begin{align*}
({{\sharp}} )
\Longrightarrow
&
\max_{ \omega \in \Omega_0 }
\frac1{{\sqrt{(2 \pi)^2 \sigma_1^2 \sigma_2^2}{}}}
\mathop{
\int}_{
\Xi_1 \times \Xi_2 }
\exp
{
[
{}- \frac{
({}{x_1} - h(\omega){})^2
}{2 \sigma_1^2}
- \frac{
({}{x_2} - {}w(\omega){})^2
}{2 \sigma_2^2}
{}]
}
d {}{x_1} d {}{x_2}
\\
\Longrightarrow
&
\max_{ \omega \in \Omega_0 }
\exp
{
[
{}- \frac{
({}{165} - h(\omega){})^2
}{2 \sigma_1^2}
- \frac{
({}{65} - {}w(\omega){})^2
}{2 \sigma_2^2}
{}]
}
\\
\Longrightarrow
&
\min_{ \omega \in \Omega_0 }
{
[
\frac{
({}{165} - h(\omega){})^2
}{2 \sigma_1^2}
+ \frac{
({}{65} - {}w(\omega){})^2
}{2 \sigma_2^2}
{}]
}
\\
&
\text{(
簡単のため,
$\sigma_1=\sigma_2$と仮定して)}
\\
\Longrightarrow
&
\text{$\omega_4$のとき,最小値}\frac{
({}{165} - 170{})^2+({}{65} - 60{})^2
}{2 \sigma_1^2}
\text{を得る.}
\end{align*}
$(\sharp):$
$
[{\widehat F}_0(\{\Xi_1 \times \Xi_2)]
(\omega
)$
を最大とするような
$\omega_0$
$(\in \Omega_0)$
を見つけよ.
さて,次に
問題13.2
を測定理論の言葉
(すなわち,回帰分析(定理13.4))で解答しよう.
解答 13.6[(問題13.2(制御問題)から続く)回帰分析]

を得ることを期待しているのであった.
十分に大きな$N$に対して,
\begin{align*}
\Xi_1 =\left[{}1.9 - \frac1{N}, 1.9 + \frac1{N}\right],
\Xi_2 =\left[{}3.0 - \frac1{N}, 3.0 + \frac1{N}\right],
\Xi_3 =\left[{}4.7 - \frac1{N}, 4.7 + \frac1{N}\right]
\end{align*}
とおいて,
フィッシャーの最尤法(定理5.6)
より,
問題13.2
は
という問題に帰着される.
$N$は十分大きな自然数と仮定しているので,
\begin{align*}
({{\sharp}} )
\Longrightarrow
&
\max_{ (\alpha, \beta{}) \in \Omega_0 }
[{\widehat F}_0(\Xi_1 \times
\Xi_2
\times
\Xi_3
)]
(\alpha, \beta{})
\\
\Longrightarrow
&
\max_{ (\alpha, \beta{}) \in \Omega_0 }
\frac1{{\sqrt{2 \pi \sigma^2}{}}^3}
\mathop{
\int\int\int}_{
\Xi_1 \times \Xi_2 \times \Xi_3 }
e^{
[{}- \frac{
({}{x_1} - (\alpha + \beta{}){})^2 +
({}{x_2} - (\alpha + 2 \beta{}){})^2 +
({}{x_3} - (\alpha + 3 \beta{}){})^2
}{2 \sigma^2}{}]
}
\\
&
\times
d {}{x_1} d {}{x_2} d {}{x_3}
\\
\Longrightarrow
&
\max_{ (\alpha, \beta{}) \in \Omega_0 }
\exp(-J/(2 \sigma^2))
\\
\Longrightarrow
&
\min_{ (\alpha, \beta{}) \in \Omega_0 } J
\end{align*}
ここに
\begin{align}
J = (1.9 -(\alpha + \beta{}){})^2 +
(3.0 - (\alpha + 2 \beta{}){})^2 +
(4.7 - (\alpha + 3 \beta{}){})^2
\end{align}
(
$
\frac{\partial J}{\partial \alpha}=0,
\frac{\partial J}{\partial \beta}=0
\text{として}
$
)
\begin{align*}
\Longrightarrow
&
\begin{cases}
(1.9 -(\alpha + \beta{}){}) +
(3.0 - (\alpha + 2 \beta{}){}) +
(4.7 - (\alpha + 3 \beta{}){}) = 0
\\
(1.9 -(\alpha + \beta{}){}) +
2 (3.0 - (\alpha + 2 \beta{}){}) +
3 (4.7 - (\alpha + 3 \beta{}){}) = 0
\end{cases}
\\
\Longrightarrow
&
\quad
(\alpha, \beta{}) =
(0.4, 1.4)
\end{align*}
$(\sharp):$
$
[{\widehat F}_0(\Xi_1 \times
\Xi_2
\times
\Xi_3
)]
(\alpha, \beta{})$
を最大とするような
$(\alpha, \beta{})$
$(=\omega_0 \in \Omega_0)$
を見つけよ.
注意13.7
$\bullet$
理論的観点からは、
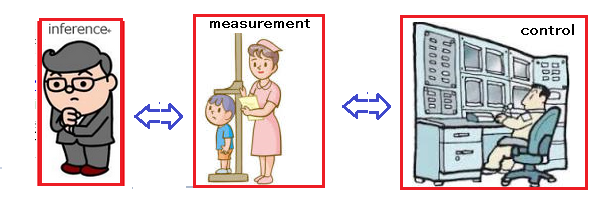
13.2:回帰分析=因果関係+フィッシャーの最尤法
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
定理 13.4 [回帰分析]
$\square \quad$
