木半順序集合
(in
12.1節(有限測定理論の因果関係)
の議論を無限測定理論に一般化する.
$(T,{{\; \leqq \;}})$ を木半順序集合, すなわち, 半順序集合で
\begin{align*}
\text{
"$t_1 {{\; \leqq \;}}t_3$
かつ
$t_2 {{\; \leqq \;}}t_3$" $\Longrightarrow$
"$t_1 {{\; \leqq \;}}t_2$
または
$t_2 {{\; \leqq \;}}t_1$"
}
\end{align*}
を満たすとする.
ただし,
ここ
では,
$T$は
有限集合とは限らないとする.
$T^2_{\leqq}= \{ (t_1,t_2) \in T^2{}: t_1 {{\; \leqq \;}}t_2 \}$
とおく.
要素 $t_0 \in T$が,
$t_0 {{\; \leqq \;}}t$ ($\forall t \in T$)
を
満たすとき,
ルート
と呼ぶ.
木半順序集合$T$はルートをもつとは限らないが,
ルートをもつ場合,しかもそれを明示したい場合は,
$T$
を
$T{(t_0)}$
と記す.
や通常の順序関係の下で,
非負実数全体$T(0)=\{ t \in {\mathbb R}
\;|\;
t {\; \geqq \;}0 \}$
とか
自然数全体$T(1)=\{1,2,\ldots
\}$
などを想定すればよい.
部分集合$T' (\subseteq T )$
が,
下に有界
とは,
$t_i {{\; \leqq \;}}t $
$(\forall t \in T')$
となる
$t_i \in T$
が存在するときを言う.
したがって,
もし$T$がルートをもつ場合は,
任意の$T' (\subseteq T )$
は,下に有界である.
統計学の本も量子力学の本も、普通は「数学でなくて算数で」書かれている。
これは、学ぶべきことで、量子言語も「算数で書かれている本・説明」が必要と考えている。
ぜひ誰かにこれを実行してもらいたい。
と考えるからである。そうでなければ、普及するわけがない。
しかし、今のところ、「以下のような数学的議論」を通過しなければ、著者にとっては気持ちが悪い。
説明される側にとっては、どうでもいいことなのかもしれないので、スキップしてもらっても構わない。
典型的な例としては,第6章
で述べた有限半順序集合:
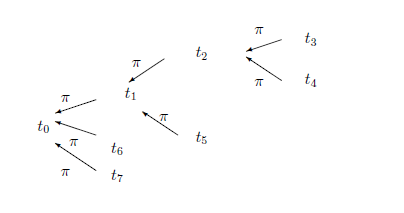
$T$は(木半順序集合の意味で)
完備
と仮定する.
すなわち,
任意の下に有界な部分集合$T' (\subseteq T )$
に対して,
次の
(i)と
(ii)を満たす${\rm Inf}_T ( T' ) (\in T )$が一意に存在すると仮定する.
$(i):$
${\rm Inf}_T ( T' ) {{\; \leqq \;}}t \qquad ( \forall t \in T' )$
ただし,
本書では,$T$の位相・距離についての
議論は省く.
$(ii):$
もし
$s {{\; \leqq \;}}t \; \; ( \forall t \in T' )$
ならば,
$s {{\; \leqq \;}}{\rm Inf}_T ( T' )$が成り立つ.
$(T{(t_0)}, {{\; \leqq \;}})$をルート$t_0$をもつ (有限または無限)木半順序集合とする. 各 ${t}\in{{T}}$に対して, 可分完備距離空間 $X_{t}$を定めて, $(X_{t} , {\cal F}_{{t}}{})$を そのボレル可測空間, ${\mathsf O}_t {{=}} (X_t, {\cal F}_t, F_t)$ を $\overline{\mathcal A}_t$ 内の 観測量 とする. すなわち, (無限)因果観測量列$[{}{\mathsf O}_{T(t_0)}{}]$ $=$ $[{}\{ {\mathsf O}_t \}_{ t \in T} , \{ \Phi_{t_1,t_2}{}: $ ${L^\infty (\Omega_{t_2}, \nu_{t_2})} \to {L^\infty (\Omega_{t_1}, \nu_{t_1})} \}_{(t_1,t_2) \in T^2_{\leqq}}$ $]$ を考える.
有限の場合 の因果観測量列(sequential causal observable)の実現化は簡単で、以下のように復習しておく:
ここで,
$\overline{\cal P}_0(T)$
$( =
\overline{\cal P}_0(T(t_0))
\subseteq {\cal P}(T) )$
を次のように定める:
\begin{align}
\overline{\cal P}_0(T(t_0))=
\{ {T'} \subseteq T \;|\;
{T'}
は有限集合,
t_0 \in T'
かつ
{\rm Inf}_{T'} S = {\rm Inf}_T S
\;\;
(\forall S \subseteq T')
\}
\tag{14.1}
\end{align}
${T'{(t_0)}} \in \overline{\cal P}_0(T{(t_0)} )$
とする.
$(T'(t_0), {{\; \leqq \;}})$
は,有限木半順序集合なので,
親写像を用いて,
$({T'} {{=}} \{ t_0, t_1,\ldots , t_N \},$
$ \pi{}: {T'} \setminus \{t_0\} \to T'{})$
と書ける.
さて,
因果観測量列
\begin{align*}
[{}\{ {\mathsf O}_t \}_{ t \in {T'}} ,
\{ \Phi_{\pi(t), t }{}:
\overline{\mathcal A}_{t}
\to
\overline{\mathcal A}_{\pi(t)}
\}_{ t \in {T'} \setminus \{t_0\} }
]
\end{align*}
を考えよう.
各 $s$
$(\in {T'}{})$に対して,
$T_s =\{ t \in T' \;|\; t {\; \geqq \;}s \}$
と定めて,
$\overline{\mathcal A}_{s}$
内の観測量
$\widehat{\mathsf O}_s {{=}} ({{{\times}}}_{t \in T_s } X_t, $
$\boxtimes_{t \in T_s } {\cal F}_t, {\widehat F}_s)$
を以下の規則で定める
($T'$が有限なので,前節と同じ議論で):
\begin{align}
\widehat{\mathsf O}_s
=
\begin{cases}
{\mathsf O}_s
\quad
&
\text{($ s \in {T'} \setminus \pi ({T'}) $ のとき)}
\\
\\
{\mathsf O}_s
{\times}
({
\underset{{t \in \pi^{-1} (\{ s \}{})}}{{{{\times}}}}
} \Phi_{ \pi(t), t}
\widehat {\mathsf O}_t{})
\quad
&
\text{($ s \in \pi ({T'}) $ のとき)}
\end{cases}
\tag{14.2}
\end{align}
これを逐次的に行なって(
量子系の場合は必ずしも可能とは限らないが),
$\widehat{\mathsf O}_{t_0}{{=}} ({{{\times}}}_{t \in T' } X_t, $
$\boxtimes_{t \in T' } {\cal F}_t, {\widehat F}_{t_0})$
を得る.これは${T'}$
$(\in \overline{\cal P}_0(T))$
に依存しているので,
\begin{align}
\widehat{\mathsf O}_{{T'}}{{=}} ({{{\times}}}_{t \in T' } X_t,
\boxtimes_{t \in T' } {\cal F}_t, {\widehat F}_{T'})
\nonumber%\tag{13.9}
\end{align}
とも記す.
無限の場合(上の有限の場合を無限に拡張)は、単なる数学的テクニックの問題で、スキップも可
たとえば、統計学だってその数学的基盤は「コルモゴロフの拡張定理」であるが、それを使いこなせる統計学者はほとんどいない。 使いこなせなくても、一流の統計学者はいくらでもいる。
- と言う意味で、以下はスキップ可
無限の場合(以下で,上の有限の場合を無限に拡張する)
任意の部分集合 $T_{1} \subseteq T_{2}( \subseteq {{T}}{})$ に対して, 自然な射影写像 $ \pi_{T_{1},T_{2}}: {{{\times}}}_{{t} \in T_{2}} X_{{t}} \longrightarrow {{{\times}}}_{{t} \in T_{1}} X_{{t}} $ を, \begin{align} {{{\times}}}_{t\in T_{2}}X_{t} \ni (x_t )_{t \in T_2 } \mapsto (x_t )_{t \in T_1} \in {{{\times}}}_{t\in T_{1}}X_{t} \tag{14.3} \end{align} によって定める.
上で定めた $ \overline{\mathcal A}_{t_0} $ 内の 観測量の族 \begin{align} \bigl\{ \widehat{\mathsf O}_{T'}{{=}} ({{{\times}}}_{t \in T' } X_t, \boxtimes_{t \in T' } {\cal F}_t, {\widehat F}_{T'}) ~|~ {T'}\in{\overline{\cal P}_0}({{T}}) \bigr\} \nonumber%\tag{13.11} \end{align}
は,
明らかに次の
一貫性条件
を満たす
(
定理4.1では,
${{\cal P}_0}({{T}})$を考えたが,
${\overline{\cal P}_0}({{T}})$
でも同様な議論ができる.)
すなわち,
| $\quad$ | $T_1 \subseteq T_2$を満たす 任意の$T_1, T_2$ ($\in$ ${\overline{\cal P}_0}({ {T}})$)に対して,次を満たす: |
したがって, 定理4.1[測定理論版のコルモゴロフの拡張定理] により, 次を満たす$\overline{\mathcal A}_{t_0}$内の観測量 ${\widehat{\mathsf O}}_{{{T}}}$ ${{=}}$ $\bigl({{{\times}}}_{{t} \in {T}}X_{{t}}, $ $\boxtimes_{{t}\in{{T}}} {\cal F}_{{t}},$ ${\widehat F}_{{T}} \bigr)$ が唯一存在する:
\begin{align} {\widehat F}_{{T}} \bigl( \pi_{{T_0, T}}^{-1}({\Xi}_{{T_0}}{}) \bigr) = {\widehat F}_{{T_0}} \bigl({\Xi}_{{T_0}} \bigr) \quad (\forall {\Xi}_{{T_0}} \in \boxtimes_{{t}\in{T_0}} {\cal F}_{{t}},~ \forall{T_0}\in{\overline{\cal P}_0}({{T}}){}) %%\t \tag{14.5} \end{align}この観測量 ${\widehat{\mathsf O}}_{{{T}}}$ ${{=}}$ $({{{\times}}}_{{t} \in {T}}X_{{t}}, $ $\boxtimes_{{t}\in{{T}}} {\cal F}_{{t}},$ ${\widehat F}_{{T}} )$ を, 因果観測量列 $[{}{\mathsf O}_{T(t_0)}{}]$ $=$ $[{}\{ {\mathsf O}_t \}_{ t \in T} ,$ $ \{ \Phi_{t_1,t_2}{}: $ ${L^\infty (\Omega_{t_2}, \nu_{t_2})} $ $\to {L^\infty (\Omega_{t_1}, \nu_{t_1})} \}_{(t_1,t_2) \in T^2_{\leqq}}$ $]$ の 実現因果観測量 と呼ぶ.
古典系に限れば、次のようにまとめることができる。
定理 14.2 [古典系における無限実現因果観測量の存在定理]
$T(=木半順序集合)$はルート$t_0$を持つとする. 各$t \in T(=木半順序集合)$に対して,古典基本構造: \begin{align*} [ C_0(\Omega_t ) \subseteq L^\infty(\Omega_t, \nu_t ) \subseteq B(L^2(\Omega_t, \nu_t ) ) ] \end{align*} を考える. 各 ${t}\in{{T}}$に対して, 可分完備距離空間 $X_{t}$, ボレル可測空間 $(X_{t} , {\cal F}_{{t}}{})$ を定める。 ここで、 因果観測量列$[{}{\mathsf O}_{T(t_0)}{}]$ $=$ $[{}\{ {\mathsf O}_t \}_{ t \in T} , \{ \Phi_{t_1,t_2}{}: $ $ L^\infty (\Omega_{t_2} ,\nu_{t_2} ) \to L^\infty (\Omega_{t_1} ,\nu_{t_1} ) \}_{(t_1,t_2) \in T^2_{\leqq}}$ $]$ を考える。 このとき、 次を満たす$L^\infty (\Omega_{t_0} ,\nu_{t_0} )$ 内の 実現因果観測量 ${\widehat{\mathsf O}}_{{{T}}}$ ${{=}}$ $\bigl(\times_{{t} \in {T}}X_{{t}}, $ $\boxtimes_{{t}\in{{T}}} {\cal F}_{{t}},$ ${\widehat F}_{{T}} \bigr)$ がただ一つ存在する:
\begin{align} {\widehat F}_{{T}} \bigl( \pi_{{{T'}, T}}^{-1}({\Xi}_{{{T'}}}) \bigr) = {\widehat F}_{{{T'}}} \bigl({\Xi}_{{{T'}}} \bigr) \quad (\forall {\Xi}_{{{T'}}} \in \boxtimes_{{t}\in{{T'}}} {\cal F}_{{t}},~ \forall{{T'}}\in{\overline{\cal P}_0}({{T}})) %%\t \tag{14.6} \end{align}
