14.2.1: 確率論におけるブラウン運動

この節では、定理14.2の応用として、ブラウン運動を量子言語で記述することを考える。 その前に、確率論の中でのブラウン運動の通常の定式化について復習しておく。







定義14.3[確率論の中でのブラウン運動の通常の定式化]


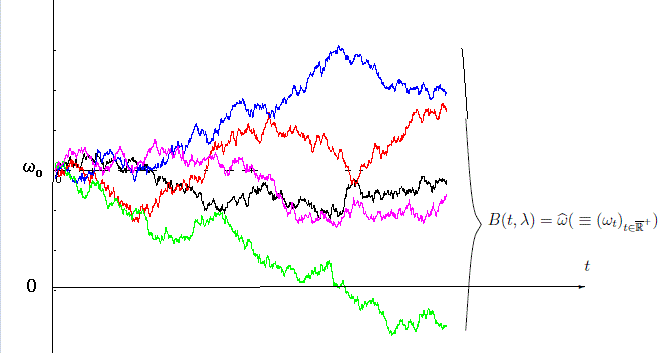
$(\Lambda, {\cal F}_\Lambda , P)$ を確率空間として， 各$\lambda \in \Lambda $ に対して， 実数値連続関数 $B(\cdot ,\lambda): T({{=}} [0, \infty)) \to {\mathbb R}$ が定まって，次を満たすとき， $B(t,\lambda)$， $( t \in T)$， を ブラウン運動 と呼ぶ． $t_0=0 < t_1 < t_2 < \cdots < t_n $ を任意として， \begin{align} & P(\{ \lambda \in \Lambda \;|\; B(t_k,\lambda) \in \Xi_k \in {\cal B}_{\mathbb R} \;\; (k=1,2,\ldots, n ) \}) \nonumber \\ =& \int_{\Xi_1 } \Big(\cdots (\int_{\Xi_{t_{n-1}}} (\int_{\Xi_{t_n}} {{{\times}}}_{k=1}^{n} G_{ \sqrt{t_{k} - t_{k-1}} } (\omega_{k} - \omega_{k-1}{}) d\omega_n) d\omega_{n-1}) \cdots \Big) d\omega_1 \tag{14.7} \end{align} ここに， $\omega_0 \in {\mathbb R}$， $ d\omega_k$ は${\mathbb R}$上のルベーグ測度， $G_{\sqrt{t}}(q) = \frac{1}{\sqrt{2\pi t}}\mbox{ exp}\left[{}- \frac{q^2}{2t} \right]$ とする.



14.2.2: 量子言語におけるブラウン運動

このブラウン運動を， 測定理論の中で定式化するならば， 以下のようになる． $({\mathbb R} , {\cal B}_{\mathbb R},m)$ をルベーグ測度空間とする． 拡散方程式： \begin{align*} \frac{\partial{\rho}_t (q)}{\partial t} = \frac{\partial^2{\rho}_t (q)}{\partial q^2}, \qquad (\forall q \in {\mathbb R}, \forall t \in T {{=}} [0,\infty ) \;) \end{align*}

を考えて， この解から， 前双対作用素列 $\{ [{}\Phi_{t_1, t_2}{}]_*$ $:$ $ L^1({\mathbb R} ,m{})$ $\to$ $ L^1({\mathbb R},m{})\}$ を次のように得る． すなわち， 任意の$\rho_1 \in L^1({\mathbb R} ,m{})$ に対して，

\begin{align*} & \big([{}\Phi_{t_1, t_2}{}]_{*} ({\rho}_{t_1}{}) \big) (q) = {\rho}_{t_2}(q) = \int_{-\infty}^{\infty} {\rho}_{t_1}(y) G_{\sqrt{t_2 - t_1} }(q - y) m(dy{}) \;\; \\ & \hspace{4cm} (\forall q \in {\mathbb R}, {}\forall (t_1 , t_2{}) \in T^2_{\leqq} {}) \end{align*} と定まる．

簡単のため，各 $t\in T {{=}} [0,\infty)$ に対して， $(\Omega_t, {\cal B}_t, d \omega_t{})$ $=$ $({\mathbb R}, {\cal B}_{\mathbb R}, m)$ とおく． $L^{\infty}(\Omega_t)$内の 精密観測量 ${\mathsf O}^{(e)}_t$ ${{=}}$ $(\Omega_t, {\cal B}_t, F^{\rm (e)}_t)$ を考える． $\Phi_{t_1 , t_2 }$ $=$ $([{}\Phi_{ t_1 , t_2 }{}]_*{})^*$ とおいて ( すなわち， $\Phi_{t_1 , t_2 }$ は ${}[{}\Phi_{ t_1 , t_2 }{}]_*{}$ の双対作用素 )， 因果精密観測量列

\begin{align*} [{}{\mathsf O}_T{}] = [{}\{ {\mathsf O}^{(e)}_t \}_{ t \in T} , \{ \Phi_{t_1,t_2}{}: {L^\infty (\Omega_{t_2}, d \omega_{t_2})} \to {L^\infty (\Omega_{t_1}, d \omega_{t_1})} \}_{(t_1,t_2) \in T^2_{\leqq}} ] \end{align*}

を得る． 定理4.1[測定理論版のコルモゴロフの 拡張定理 ] により， 実現因果観測量を$\widehat{\mathsf O}_{T}$ $=({{{\times}}}_{t \in T} \Omega_t, \boxtimes_{t \in T} {\cal B}_t,$ $ {\widehat F}_T )$ を構成して， 測定 ${{\mathsf M}}_{L^\infty(\Omega_0) } ( \widehat{\mathsf O}_{ T} , S_{[\omega_0]}{})$ を得る．
さて， 次を仮定する:

$\quad$ 測定 ${{\mathsf M}}_{L^\infty(\Omega_0) } ( \widehat{\mathsf O}_{ T} , S_{[\omega_0]}{})$ により 測定値 ${\widetilde x}$ $(=(x_t)_{t\in {T} } \in {{{\times}}}_{t\in T} \Omega_t ={\mathbb R}^T)$ が得られた．

ここで， 測定値 ${\widetilde x}$ $(=(x_t)_{t\in {T} } \in {\mathbb R}^T )$ の性質について考えよう．
$t_0=0 < t_1 < t_2 < \cdots < t_n $ として， $D=\{ t_1,t_2,\ldots,t_n\}$とおく． また， ${\widetilde\Xi}=\mbox{ ${{{\times}}}$}_{t\in {T} }^D\Xi_t$ $=$ $({{{\times}}}_{t\in D} \Xi_t ) \times ({{{\times}}}_{t\in T\setminus D} X_t ) $ $\bigl(\in{\cal B}_{\mathbb R}^{ {T} }\bigl)$ とおく． このとき， 測定値${\widetilde x} (=(x_t)_{t\in {T} }{}) $ が ${\widetilde\Xi} {{=}} \mbox{ ${{{\times}}}$}_{t\in T }^D\Xi_t$ に属する確率は，言語ルール1(2.7節)により，

\begin{align} & \bigl({\widehat F}_{T} ({\widetilde\Xi}) \bigr) (\omega_0) = \Big(F(\Xi_{0}) \Phi_{ 0 , t_1 } \Big(F(\Xi_{t_1}) \cdots \Phi_{ t_{n-2} , t_{n-1}} \Big( F(\Xi_{t_{n-1}}) \nonumber \\ & \hspace{6cm} \times \bigl(\Phi_{t_{n-1} , t_n} F(\Xi_{t_n} {}) \bigl) \Big) \Big) \Big)(\omega_0) \nonumber \\ =& \int_{\Xi_1 } \Big(\cdots (\int_{\Xi_{t_{n-1}}} (\int_{\Xi_{t_n}} {{{\times}}}_{k=1}^{n} G_{ \sqrt{t_{k} - t_{k-1}} } (\omega_{k} - \omega_{k-1}{}) d\omega_n) d\omega_{n-1}) \cdots \Big) d\omega_1 \tag{14.8} \end{align}

となる． ここで， (14.7)=(14.8) であるから， これは ブラウン運動$B(t, \lambda )$ と数学的には 同じであることがわかる． すなわち、つぎの同一視を得る：

\begin{align*} \overset{\mbox{ 確率論}}{\underset{\mbox{ ブラウン運動}}{\fbox{$ \Big( B(t, \cdot ) \Big)_{t \in T}$ }} } = \overset{\mbox{ 量子言語}}{\underset{\mbox{ 測定値}}{\fbox{$ \Big( \widehat{\omega}_t \Big)_{t \in T}$ }} } \end{align*}


$\fbox{注釈14.1}$ したがって， 測定理論の原則 に固執して言うならば，

$\bullet$ ブラウン運動は，「運動」ではなくて，精密測定値列ということになる。


パルメニデスの「運動は存在しない」を思い出そう． 繰り返しになるが 言語的コペンハーゲン解釈によれば、
$(\sharp_1):$ 「多数」を「単一」のように記述せよ。
$(\sharp_2):$ 「動いているもの」を「静止しているもの」のように 記述せよ。　時間経過などないように記述せよ。
である。 なぜ、$(\sharp_1)$や$(\sharp_2)$に固執しなければならないのかの理由は、結果論でしかないのかもしれない。 ただし、次の問題を考えてみよう：
$(\flat):$ 「怒られないと、勉強しない」 の対偶を述べよ
もちろん、高校生パズルで、そんなに難しくはないが、 それでも、
  • 「時間」と「論理」の相性の悪さを実感できる
だろう。