この節では、
ゼノンのパラドックス
---
最古の科学パラドックス
---
について議論する。
すなわち,
を議論する。
14.4.1: ゼノンのパラドックスとは何か?
ゼノンのパラドックスとしては、"アキレスと亀"と"飛ぶ矢"が有名かもしれないが、
他にも、
"二分法", "競技場"
などがある。
これらは、「すべて同じ種類の問題」と考える。
したがって、一つが解ければ、他も同様に解ける。
一番の傑作は、"飛ぶ矢"と思うが、"アキレスと亀"も有名なので、
この節では、この二つについて議論する。
以下は、ゼノンが提示した「ゼノンのパラドックス」である。
パラドックス14.9 [ゼノンのパラドックス]
 [飛ぶ矢]
[飛ぶ矢]
| $\bullet$ |
矢が飛んでいるとしよう.
この矢は,いつの時点でもその瞬間は止まっている.
いつの時点でもその瞬間は止まっているならば,
いつも止まっているわけで,
したがって,矢は止まっていて動かない.
|
[アキレスと亀]
「アキレスと亀のパラドックス」についてのゼノンの論法は以下の通りである:,
| $\bullet$ |
アキレスと亀の競争を考える.アキレス(
速い走者)のスタート点より,亀(遅い走者)のスタート点
は前方とする.
「よーい.ドン」で両者が同時にスタートしたとしよう.
このとき,
アキレスが亀に追い抜こうとするならば,
アキレスは, いま亀がいるところまで行かなければならない.
そうしたとしてもそのときは, 亀がもっと先に行ってるはずである.
アキレスは, 更にいま亀がいるところまで行かなければならない.
これを限りなく続けても,
決してアキレスは亀に追いつくことができない.
|
注意点
ゼノンのパラドックスは、現代的意味においても、哲学(世界記述)の主要テーマの一つであるが、
もちろん、「無限等比級数を理解できない馬鹿な哲学者が議論している」わけではない。
| $\bullet$ |
並の数学者よりは数学のできる哲学者が議論している
|
のである。
2500年以上も、哲学者たちの心を捉えつづけた未解決問題であるが、
その
「解答のパターン」は決まっている。 すなわち、
| $\bullet$ |
ある世界記述法を提案して、その記述法で、ゼノンのパラドックスを記述する
|
である。
これは、当然のことで、「哲学者の仕事=世界記述法の提案」だからである。
さて、
に答えるために、
本書の主張である次の図を確認しておこう。
もちろん、我々の主張は、
-
ゼノンのパラドックスは、この図(世界記述の発展史)無くして、解けない
だからである。
図14.10 [=図1.1 in $\S$1.1:
世界記述の発展史]
さて、
| $(A):$ |
デカルト=カント哲学や
言語哲学では、
ゼノンのパラドックス14.9
に答える力はない
|
ことは、明らかであるが、次の問いかけは考察するに値する:
| $(B_1):$ |
ゼノンのパラドックス14.9
をニュートン力学という言語で答えよ。
|
| $(B_2):$ |
ゼノンのパラドックス14.9
を量子力学という言語で答えよ。
|
| $(B_3):$ |
ゼノンのパラドックス14.9
を相対性理論という言語で答えよ。
|
| $(B_4):$ |
ゼノンのパラドックス14.9
を統計学(=動的システム理論)という言語で答えよ。
|
| $(B_5):$ |
ゼノンのパラドックス14.9
を量子言語で答えよ。
|
さて、上の(B$_1$)--(B$_5$)では、多少無理気味なものもあるが、それでも強引に答えることは可能だろう。そうならば、次の問いかけをしたくなる。
| $(C):$ |
上の(B$_1$)--(B$_5$)で、もっとも自然なのはどれか?
|
ここで、次のように考える:
| $(D):$ |
"ゼノンのパラドックス14.9
を解く"
$\Longleftrightarrow$
"問題(C)に答える"
|
もちろん、我々の主張は、
| $(E):$ |
問題(C)の答えは、
量子言語による解答(B$_5$)である
|
となる。
以上をまとめると:
問題14.11[ゼノンのパラドックスの意味]
ゼノンのパラドックスの意味
| $\quad$ |
$\qquad$"飛ぶ矢"と"アキレスと亀"を(古典)量子言語で記述せよ!
|
である。
14.4.2:$(B_4)$の解答(
動的システム理論によるゼノンのパラドックスの解答)
問題 14.11を解く前に、
問題(B$_4$)
--
動的システム理論による解答
--
を解いておく。
このために、
動的システム理論の基礎を述べておく。
14.4.2.1: 動的システム理論の定式化
動的システム理論(=統計学)は、主に工学として発展してきたので、「定式化」にあまり注意を払わないのが普通であるが、
大部分の研究者の共通部分的な定式化として、次は認めよう。
定式化14.12 [動的システム理論の定式化]
動的システム理論は次のように定式化される:
\begin{align}
\underset{\mbox{}}{\fbox{動的システム理論}}
=
\underset{\mbox{}}{\fbox{①:状態方程式}}
+
\underset{\mbox{}}{\fbox{②:測定方程式}}
\tag{14.9}
\end{align}
①
:
$
\underset{\mbox{}}{\fbox{状態方程式}}
$
は次のように定まる:
$T={\mathbb R}$を時間軸とする。
各$t ( \in T)$に対して、
状態空間を
$\Omega_t = {\mathbb R }^n$
($n$-次元実空間).とする。
このとき、
状態方程式
(第13章の(13.2)式)
は、次の連立一階微分方程式として定義される:
\begin{align}
&
\underset{\mbox{}}{\fbox{状態方程式}}
=
\begin{cases}
\frac{d\omega_1}{dt}{} (t)=v_1(\omega_1(t),\omega_2(t),\ldots,\omega_n(t),\epsilon_1(t), t)
\\
\frac{d\omega_2}{dt}{} (t)=v_2(\omega_1(t),\omega_2(t),\ldots,\omega_n(t),\epsilon_2(t), t)
\\
\cdots \cdots
\\
\frac{d\omega_n}{dt}{} (t)=v_n (\omega_1(t),\omega_2(t),\ldots,\omega_n(t), \epsilon_n(t),t)
\end{cases}
\tag{14.10}
\end{align}
ここに
$\epsilon_k(t)$
は雑音
($k=1,2, \cdots, n $).
②
:
$
\underset{\mbox{}}{\fbox{測定方程式}}
$
は次で定める:
$X = {\mathbb R }^m$
($m$-次元実空間)を測定空間とする。
測定方程式
(第13章の(13.2)式)
は次のように定める:
\begin{align}
&
\underset{\mbox{}}{\fbox{測定方程式}}
=
\begin{cases}
x_1(t)=f_1(\omega_1(t),\omega_2(t),\ldots,\omega_n(t),\eta_1(t), t)
\\
x_2(t)=f_2(\omega_1(t),\omega_2(t),\ldots,\eta_n(t),\eta_2(t), t)
\\
\cdots \cdots
\\
x_m(t) =f_m (\omega_1(t),\omega_2(t),\ldots,\eta_n(t), \eta_n(t),t)
\end{cases}
\tag{14.11}
\end{align}
ここに
$\eta_k(t)$
は測定誤差
($k=1,2, \cdots, m $).
$x(t)(=(x_1(t), x_2(t), \cdots, x_n(t)))$
は運動関数と呼ぶ。
14.4.2.2: 動的システム理論によるゼノンのパラドックスの解答(=小学生の解答=旅人算(距離=速さ$\times$時間))
運動関数(距離=速さ$\times$時間)を使う解法を、旅人算という。
解答 14.13[動的システム理論によるゼノンのパラドックス(飛ぶ矢)の解答]
時刻$t$における矢の位置を$q(t)$とする.
すなわち,
運動関数$x=q(t)$
を考える.
| $\bullet$ |
各時刻$t$において,矢の位置は$q(t)$となるとしても,
それが,
運動関数$q(t)$が定数関数であることを意味しない
|
よって,ゼノンの論法14.9は間違っている.
 解答 14.13[動的システム理論によるゼノンのパラドックス(アキレスと亀)の解答
(=小学生の解答)
]
解答 14.13[動的システム理論によるゼノンのパラドックス(アキレスと亀)の解答
(=小学生の解答)
]
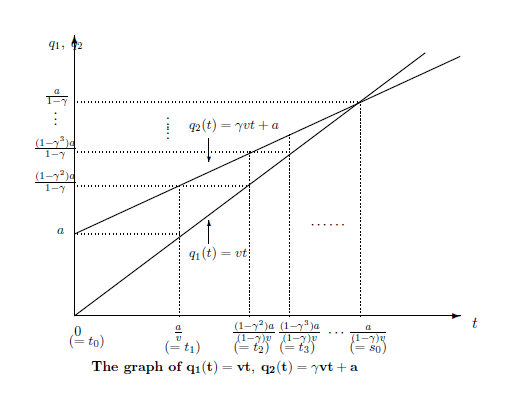
アキレスと亀の運動関数
\begin{align}
x=q_1(t)=vt, \qquad y=q_2(t)=\gamma vt +a
\tag{14.12}
\end{align}
とする
(ここに,
$0 < \gamma v < v$,
$a >0$).
(i):[代数的解答]
これを代数的に解くことは簡単で,
$q_1(s_0)=q_2(s_0)$の解は,
\begin{align*}
s_0=\frac{a}{(1- \gamma ) v}
\end{align*}
となるから,
時刻$s_0=\frac{a}{(1- \gamma ) v}$でアキレスは亀に追いつくことができる.
(ii):[無限等比級数による解答]
これを無限等比級数を使って、 次のように解くこともできる.
\begin{align}
s_0=\frac{a}{v}(1+\gamma + \gamma^2 + \gamma^3 +... )= \frac{a}{(1- \gamma ) v}
\tag{14.13}
\end{align}
と計算できる.
補足:
世界記述の観点からは、
問題点は(14.12)式以前である。
(14.12)式以後は、単なる計算に過ぎない。
14.4.2.3:なぜ解答14.13は、承認されないのか?: 量子言語による解答
解答14.13は間違っているわけではない。
というより、極めて常識的な解答だと思う。つまり、
と思う。
しかし、そうだとすると、次の疑問が出てくる。
| $(F):$ |
なぜ解答14.13(小学生の解答)は、ゼノンのパラドックスの決定的な解答として承認されないのか?
|
である。
疑問(F)に対しては、つぎの理由しかないと思う。
一言で言うと
-
旅人算(距離=速さ$\times$時間)は、形而上学だからダメ
である。
つまり、
| $(G_1):$ |
動的システム理論(=統計学)が世界記述法として承認されていない。
すなわち、
図14.10
(の統計学)が承認されていない。
|
または、同じ意味で、
| $(G_2):$ |
図14.10
の
言語的科学観が承認されていない。
|
である。事実、
「形而上学=非科学的」という迷信
が我々の科学観には蔓延している。
そうだとすると、
| $(H_1):$ |
本書の目的は、図14.10
の言語的科学観を主張すること
|
なのだから、本書の立場からすれば、
| $(H_2):$ |
もうすでに、ゼノンのパラドックスは
(動的システム理論という世界記述法によって)解決されている
|
と主張するしかない。
さらに、
なにか付け加えることがあるとしたら、ゼノンのパラドックス
を(動的システム理論の最終形態である)
量子言語で記述することだけで、
これを下記で述べる。
解答 14.14 [ゼノンのパラドックスに対する量子言語による解答]
問題14.11の解答
または、
問題14.9(飛ぶ矢)の解答:
系14.7(in $\S$14.4)の中で、
\begin{align*}
q(t)=y_t( = f_t(\phi_{{t_0},t } (\omega_{t_0} )))
\end{align*}
とおいて、運動関数
$q(t)$
を定めればよい。
また、
"アキレスと亀"等の解答も同様なので、
"飛ぶ矢"の解答だけで十分だろう。
| $\fbox{注釈14.2}$ |
したがって、
本書の立場では、
次の
($\sharp_1$)
と($\sharp_2$)
を
同値
と考える:
| $(\sharp_1):$ |
図14.10(右図)を受け入れる
|
| $(\sharp_2):$ |
解答14.14をゼノンのパラドックスの最終解答として受け入れる
|

ゼノン(BC. 490-430)はも昔のギリシャの哲学者なのだから、
| $(\sharp_3):$ |
"ゼノンが如何に考えたか?"
は重要とは思わない。本書は、科学哲学史の本ではない。
しかし、ゼノンはパルメニデスの弟子なのだから、
「世界記述と運動」以外のことを考えるわけがない。
|
もちろん、
| $(\sharp_4):$ |
重要なことは、
"ゼノンのパラドックスを我々が如何に考えるか?"
である
|
単純に考えて、
-
2500年間も考え続けるに値する問題は、
世界記述の問題
と
食糧問題
しかない。
すなわち、
ゼノンのパラドックスについては、多くの哲学者が議論しているが、
図14.10の提案なしには、正解はないと考える。
|