(15.3)式を
$\beta_0$と
$\beta_1 $
で偏微分して,
そして,
次の方程式
(i.e.,
"正規方程式"
)
を得る.
\begin{align}
&
\frac{\partial \sigma_{}^2
(\beta_1, \beta_2)}{\partial \beta_0}
=
{\sum_{{i}=1}^{n} ({}x_{i} - \beta_0 - \beta_1 {a}_{i}{})}=0,
\quad
({i}=1,...,{n})
\tag{15.4}
\\
&
\frac{\partial \sigma_{}^2
(\beta_1, \beta_2)}{\partial \beta_1}
=
{\sum_{{i}=1}^{n} ({}x_{i} - \beta_0 - \beta_1 {a}_{i}{}){a}_{i}}=0,
\quad
({i}=1,...,{n})
\tag{15.5}
\end{align}
これを解いて,次を得る.
\begin{align}
&
\hat{\beta}_1
=
\frac{s_{{a}x}}{s_{{a}{a}}},
\quad
\hat{\beta}_0 =
\overline{x}-\frac{s_{{a}x}}{s_{{a}{a}}}\overline{{a}},
\quad
\hat{\sigma}^2
(
=
\frac{1}{{n}}
\sum_{{i}=1}^{n}
(
x_{i} -( \hat{\beta}_1 {a}_{i} + \hat{\beta}_0 ))^2
\Big)
=
s_{xx} - \frac{s_{{a}x}^2}{s_{{a}{a}}}
\tag{15.6}
\end{align}
ここで,
\begin{align}
&
{\bar {a}}=\frac{{a}_1 + \cdots + {a}_{n}}{{n}}, \qquad
{\bar x}=\frac{x_1 + \cdots + x_{n}}{{n}},\qquad
\tag{15.7}
\\
&
s_{{a}{a}}=\frac{({a}_1 -{\bar {a}})^2 + \cdots + ({a}_{n} - {\bar {a}})^2}{{n}},
\quad
s_{xx}=\frac{(x_1 -{\bar x})^2 + \cdots + (x_{n} - {\bar x})^2}{{n}},
\quad
\tag{15.8}
\\
&
s_{{a}x}=\frac{({a}_1 -{\bar {a}})(x_1 -{\bar x}) + \cdots +
({a}_{n} - {\bar {a}})(x_{n} - {\bar x})}{{n}}.
\tag{15.9}
\end{align}
「最小二乗法」の意味は,「小話・小技」としては誰もが気分としてわかっていることと思う. しかし,「統計学」という「大きな物語」の中での「最小二乗法」の意味づけはそんなに簡単なことではないが,この意味づけが,「(統計学的)回帰分析」である. しかし,
この講義全体を通しての主張は,
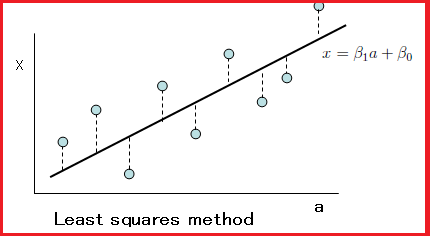 15.1:最小二乗法(簡単すぎて,かえって難しい)
15.1:最小二乗法(簡単すぎて,かえって難しい)
初等的とされている「最小二乗法」から始めよう.
2次元平面${\mathbb R}^2(\equiv \{(a,x)\;:\; a,x \in {\mathbb R} \})$内の点列
\begin{align*}
\{ ({a}_{i}, x_{i} )\}_{{i}=1}^{n}
\end{align*}
を考える.
任意の二つ実数$\beta_1$と$\beta_2$に対して,一次関数
$\phi^{(\beta_1, \beta_2)}: {\mathbb R} \to {\mathbb R}$
を以下のように定める.
\begin{align}
{\mathbb R} \ni a \mapsto
x= \phi^{(\beta_1, \beta_2)}({a})
=\beta_1 {a} + \beta_0 \in {\mathbb R}
\tag{15.1}
\end{align}
ここで,対
$(\beta_1, \beta_2) (\in {\mathbb R}^2 )$
は未知としよう.
さて,誤差$\sigma$
を次のように定める.
$\quad$
次の(15.3)式を満たす$(\hat{\beta}_0, \hat{\beta}_1)$
$( \in {\mathbb R}^2 )$を見つけよ.
\begin{align}
&
\sigma_{}^2
(\hat{\beta}_0, \hat{\beta}_1)
=
\min_{(\beta_1, \beta_2)
\in {\mathbb R}^2
}
\sigma_{}^2
(\beta_1, \beta_2)
\Big(
\equiv
\frac{1}{{n}}
\min_{(\beta_1, \beta_2)
\in {\mathbb R}^2
}
\sum_{{i}=1}^{n}
(
x_{i} -( \beta_1 {a}_{i} + \beta_0 ))^2
\Big)
\\
&
\tag{15.3}
\end{align}
この解
$(\hat{\beta}_0, \hat{\beta}_1)$
のことを
"単純回帰係数"
とよぶ.
中学生でも出来る簡単な問題であるが、偏微分を使った方が
簡単に解くことができるので、これを以下に示そう。
注意15.2 [応用数学]
さて、
であった.
そうならば,この章のすべきことは,
$\bullet$
すべてを(統計学ではなくて)量子言語で記述せよ
である.
つまり、
$\bullet$
「最小二乗法」という技法を量子言語の言葉で意味づけをせよ.
のである。
もっと正確に言えば、
である。
15.1 最小二乗法(簡単すぎて,かえって難しい)
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
問題15.1:[最小二乗法]
