栤戣15.8:[堦斒壔慄宍儌僨儖偺(検巕尵岅偵傛傞)掕幃壔]
忬懺
$
(\beta_0, \beta_1,\cdots, \beta_n, \sigma_{}^2
)$
偼枹抦偲偟偰,
應掕
${\mathsf M}_{L^\infty (\Omega_{0} \times {\mathbb R}_+)}(
{\mathsf O} \equiv (X, {\cal F}, F)
, S_{[(\beta_0, \beta_1,\cdots, \beta_n, \sigma_{}^2
)]}
{}
)$偵傛偭偰,
應掕抣
$x=\begin{bmatrix}
x_1
\\
x_2
\\
\vdots
\\
x_n
\end{bmatrix}
( \in X={\mathbb R}^n )$
偑摼傜傟偨偲偟傛偆(偙偺應掕抣偺偙偲傪丄
栚揑曄悢
偲偄偆).丂
偙偺偲偒,忬懺
$
(\beta_0, \beta_1,\cdots, \beta_n, \sigma_{}^2
)$
傪應掕抣$
x=(
x_1, x_2, \ldots, x_n )
(\in {\mathbb R}^{n})$偐傜悇掕偣傛.
変乆偺栚揑偼,堦斒慄宍壔儌僨儖傪栤戣15.8
偲偟偰,掕幃壔偡傞偙偲偱偁傞.
偟偨偑偭偰,夝摎偼懠彂傪傒傛.
拲堄15.9
夞婣暘愅偺堦斒壔偲偟偰,変乆偼堦斒慄宍壔儌僨儖偵偨偳傝拝偄偨.
夞婣暘愅偺奼挘偲偟偰乽應掕岆嵎儌僨儖(measurement error model, cf.
暥專S. Ishikawa,
Mathematical Foundations of Measurement Theory,
Keio University Press Inc.
2006.
偺5.5愡(117儁乕僕))乿傕桳椡偱偁傞丅
偡側傢偪
\begin{align}
\underset{\mbox{}}{\fbox{夞婣暘愅}}
\xrightarrow[\mbox{堦斒壔}]{}
\begin{cases}
嘆:
\underset{\mbox{}}{\fbox{堦斒慄宍壔儌僨儖}}
\\
嘇:\underset{\mbox{}}{\fbox{應掕岆嵎儌僨儖}}
\end{cases}
\label{eq15.46}
\end{align}
偱偁傞丅
偟偐偟丄
堦斒慄宍壔儌僨儖偑杮嬝偱偁傞.
廤崌$T=\{ 0,1,2, \cdots, i , \cdots, n \}$偼
師偺敿弴彉峔憿傪帩偮偲偟傛偆.
\begin{align*}
0 < i
\qquad(i=1,2, \cdots, n)
\end{align*}
摨偠堄枴偱,栘峔憿
$(T, \tau: T \setminus \{0\} \to T )$
偵偍偄偰,幨憸$\tau: T \setminus \{0\} \to T$偑師傪枮偨偡丗
\begin{align}
\tau(i)=0
\qquad
(\forall i =1,2, \cdots, n)
\tag{15.36}
\end{align}
偲峫偊偰傕傛偄.
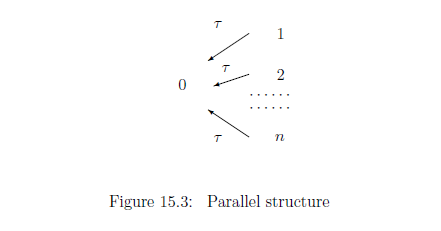
奺 $i \in T$偵懳偟偰,
嬊強僐儞僷僋僩嬻娫 $\Omega_i$傪師偺傛偆偵掕傔傞.
\begin{align}
&
\Omega_{0}={\mathbb R}^{m+1}
=
\Big\{
\beta
=\begin{bmatrix}
\beta_0 \\
\beta_1 \\
\vdots
\\
\beta_m
\end{bmatrix}
\;:\;
\beta_0, \beta_1, \cdots, \beta_m \in {\mathbb R}
\Big\}
\quad
\tag{15.37}
\\
&
\Omega_{i}={\mathbb R}
=
\Big\{
\mu_i
\;:\;
\mu_i \in {\mathbb R}
\Big\}
\quad(i=1,2, \cdots, n )
\tag{15.38}
\end{align}
擇廳悢楍
$\{ a_{ij} \}_{i=1, \cdots, n, \; j=1,\cdots, m}$傪屌掕偡傞.
偡側傢偪,
\begin{align}
a_{ij} \in {\mathbb R}
\qquad
(i=1,2, \cdots, n, \;\;j=1,2, \cdots, m, (m+1 \le n) )
\tag{15.39}
\end{align}
\begin{align}
a_i \in {\mathbb R}
\qquad
(i=1,2, \cdots, n ),
\nonumber%\tag{15.39}
\end{align}
奺$\{a_{ij} \}_{j=1, \cdots, m}$(偙傟偼捠忢偺摑寁妛偱偼
乽愢柧曄悢乿
偲屇偽傟傞)偵懳偟偰,寛掕場壥幨憸
$\psi_{a_{i \tiny{\bullet}}}: \Omega_0(={\mathbb R}^{m+1})
\to
\Omega_{i} (={\mathbb R})$
傪埲壓偺傛偆偵掕傔傞.
\begin{align}
&
\Omega_0={\mathbb R}^{m+1} \ni \beta =(\beta_0, \beta_1, \cdots, \beta_m ) \mapsto
\psi_{a_{i \tiny{\bullet}}} ( \beta_0, \beta_1, \cdots, \beta_m )
=
\beta_0 + \sum_{j=1}^m \beta_j a_{ij}= \mu_i \in \Omega_i ={\mathbb R}
\tag{15.40}
\\
&
\qquad \qquad \qquad \qquad
\qquad \qquad \qquad \qquad
(i=1,2, \cdots, n)
\nonumber
\end{align}
偙傟傪傑偲傔偰彂偔偲,
\begin{align}
\beta=
\begin{bmatrix}
\beta_0 \\
\beta_1
\\
\beta_2 \\
\vdots
\\
\beta_m
\end{bmatrix}
\mapsto
\begin{bmatrix}
\psi_{a_{1 \tiny{\bullet}}} ( \beta_0, \beta_1, \cdots, \beta_m) \\
\psi_{a_{2 \tiny{\bullet}}} ( \beta_0, \beta_1, \cdots, \beta_m)
\\
\psi_{a_{3 \tiny{\bullet}}} ( \beta_0, \beta_1, \cdots, \beta_m) \\
\vdots
\\
\psi_{a_{n \tiny{\bullet}}} ( \beta_0, \beta_1, \cdots, \beta_m)
\end{bmatrix}
=
\begin{bmatrix}
1 & a_{1{1}} & a_{12} & \cdots & a_{1m}
\\
1 & a_{2{1}} & a_{22} & \cdots & a_{2m}
\\
1 & a_{3{1}} & a_{32} & \cdots & a_{3m}
\\
1 & a_{4{1}} & a_{42} & \cdots & a_{4m}
\\
\vdots & \vdots & \vdots & \vdots & \vdots
\\
1 & a_{n{1}} & a_{n2} & \cdots & a_{nm}
\end{bmatrix}
\cdot
\begin{bmatrix}
\beta_0 \\
\beta_1
\\
\beta_2 \\
\vdots
\\
\beta_m
\end{bmatrix}
\tag{15.41}
\end{align}
偲側傞.
傑偨,偙傟偼師偺寛掕儅儖僐僼 嶌梡慺
$\Psi_{a_{i \tiny{\bullet} }}:
L^\infty(\Omega_{i}) \to L^\infty(\Omega_0)$
偲摨抣偱偁傞.
\begin{align}
[{\Psi_{a_{i \tiny{\bullet} }}}(f_i)](\omega_0)
=
f_i( \psi_{a_{i \tiny{\bullet} }} (\omega_0))
\quad
(\forall f_i \in L^\infty(\Omega_{i}),
\;\;
\forall \omega_0 \in \Omega_0,
\forall i \in 1,2, \cdots, n)
\tag{15.42}
\end{align}
偟偨偑偭偰,摨堦帇丗$\{a_{ij} \}_{j=1, \cdots, m} \Leftrightarrow \Psi_{a_{i \tiny{\bullet}}}$偺壓偱,
"愢柧曄悢"偼場壥娭學傪昞偡偲峫偊傞.

偟偨偑偭偰, 師偺娤應検
${\mathsf O}_{0}^{a_{i \tiny{\bullet} }} {{\equiv}} ({\mathbb R}, {\cal B}_{{\mathbb R}}, \Psi_{a_{i \tiny{\bullet} }}G_{\sigma_{}})$
( in
$L^\infty (\Omega_{0}(\equiv
{\mathbb R}^{m+1}))$
)傪摼傞.
\begin{align}
&
[\Psi_{a_{i \tiny{\bullet} }}(G_{\sigma_{}}(\Xi))] (\beta ) =
[(G_{\sigma_{}}(\Xi))] (\psi_{a_{i \tiny{\bullet} }}(\beta ))
=
\frac{1}{(\sqrt{2 \pi \sigma_{}^2})}
\underset{\Xi}{\int} \exp
\Big[{- \frac{ (x - (\beta_0 + \sum_{j=1}^m a_{i{j}} \beta_j ))^2}{2 \sigma_{}^2}}
\Big] dx
\\
&
\qquad
\qquad
(\forall \Xi \in {\cal B}_{{\mathbb R}}, \forall
\beta
=(\beta_0, \beta_1, \cdots, \beta_m )\in \Omega_{0} (\equiv {\mathbb R}^{m+1}
))
\tag{15.43}
\end{align}
傛偭偰, 偙傟傜偺摨帪娤應検
${\mathop{\mbox{ $\times$}}}_{i=1}^n{\mathsf O}_{0}^{a_{i \tiny{\bullet} }} {{\equiv}} ({\mathbb R}^n, {\cal B}_{{\mathbb R}^n}, {\mathop{\mbox{ $\times$}}}_{i=1}^n \Psi_{a_{i \tiny{\bullet} }}G_{\sigma_{}})$
(in
$L^\infty (\Omega_{0}(\equiv
{\mathbb R}^{m+1}))$)
偑師偺傛偆偵掕傑傞.
\begin{align}
&
[({\mathop{\mbox{ $\times$}}}_{i=1}^n \Psi_{a_{i \tiny{\bullet} }}G_{\sigma_{}})
({\mathop{\mbox{ $\times$}}}_{i=1}^n \Xi_i)](\beta)
=
{\mathop{\mbox{ $\times$}}}_{i=1}^n \Big(
[\Psi_{a_{i \tiny{\bullet} }}G_{\sigma_{}})
(\Xi_i)](\beta)\Big)
\nonumber
\\
=
&
\frac{1}{(\sqrt{2 \pi \sigma_{}^2})^n}
\underset{{\mathop{\mbox{ $\times$}}}_{i=1}^n \Xi_i}{\int \cdots \int} \exp
\Big[{- \frac{ \sum_{i=1}^n (x_i - (\beta_0 + \sum_{j=1}^ma_{i{j}} \beta_j ))^2}{2 \sigma_{}^2}}
\Big] dx_1 \cdots dx_n
\tag{15.44}
\\
&
\qquad
\qquad
(\forall {\mathop{\mbox{ $\times$}}}_{i=1}^n \Xi_i \in {\cal B}_{{\mathbb R}^n}, \forall
\beta
=(\beta_0, \beta_1, \cdots, \beta_m )
\in \Omega_{0} (\equiv {\mathbb R}^{m+1} ))
\nonumber
\end{align}
偙偙偱,$\sigma$傪僷儔儊乕僞曄悢偲尒偰,師偺娤應検
${\mathsf O}=
\Big({\mathbb R}^n(=X) , {\mathcal B}_{{\mathbb R}^n}(={\mathcal F}),
F \Big)$
(in $L^\infty ( \Omega_0 \times {\mathbb R}_+ )$)
傪摼傞.
\begin{align}
&
\small{
[F({\mathop{\mbox{ $\times$}}}_{i=1}^n \Xi_i )](\beta, \sigma_{})
=
[({\mathop{\mbox{ $\times$}}}_{i=1}^n \Psi_{a_{i \tiny{\bullet} }}G_{\sigma_{}})
({\mathop{\mbox{ $\times$}}}_{i=1}^n \Xi_i)](\beta)
\quad
(\forall {\mathop{\mbox{ $\times$}}}_{i=1}^n \Xi_i \in {\cal B}_{{\mathbb R}^n},
\forall
(\beta , \sigma_{} ) \in {\mathbb R}^{m+1} (\equiv \Omega_0) \times {\mathbb R}_+ )
}
\\
&
\tag{15.45}
\end{align}
傛偭偰,師偺栤戣傪摼傞.
15.4:堦斒壔慄宍儌僨儖
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
丂
丂丂
