17.1: テストの信頼性(心理統計)

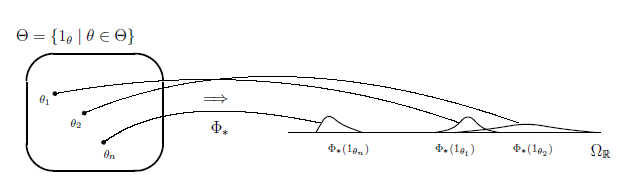
まず、 生徒グループに対する(数学の)テストの信頼性について考える。 生徒の集合を、 $\Theta := \{\theta_1,\theta_2,\dots,\theta_n\}$とする。 $\Theta$内の個数測度$\nu_c$を \begin{align*} \nu_c(\{\theta_i\}) = 1 \quad (i=1,2,\dots,n) \end{align*} で定める。 $\Theta$を状態空間と見なす。 各$\theta_i \;(\in \Theta)$に対して、 関数$1_{\theta_i} \;(\in L_{+1}^1(\Theta,\nu_c))$を次のように定める： \begin{align*} 1_{\theta_i}(\theta) = 1 \;(\text{if } \theta = \theta_i), \;\; = 0 \;(\text{if }\theta \ne \theta_i) \end{align*} まずは、簡単な場合, すなわち、 ある生徒$\omega_i$ ($\in \Theta $) に関するテストについて考えよう。 $\Omega_{\mathbb R} = {\mathbb R}$として、 ルベーグ測度空間$(\Omega_{\mathbb R},{\cal F}_{\Omega_{\mathbb R}},d\omega)$を考える。

例 17.1 (学生$\theta_i$に対するテスト)

(ある生徒$\theta_i$に対する数学のテスト) \; 生徒の集合$\Theta := \{\theta_1,\theta_2,\dots,\theta_n\}$と状態空間とする。 各生徒$\theta_i \;(\in \Theta)$に対して、 混合状態$\Phi_\ast(1_{\theta_i}) \;(\in L_{+1}^1(\Omega_{\mathbb R},d\omega))$ ($i=1,2,\dots,n$)が定まると仮定しよう。 すなわち、 マルコフ因果作用素$\Phi : L^\infty(\Omega_{\mathbb R},d\omega) \to L^\infty(\Theta,\nu_c)$ が定まっていて、その前共役作用素$\Phi_\ast : L^1(\Theta,\nu_c) \to L^1(\Omega_{\mathbb R},d\omega)$を考える。

$L^\infty(\Omega_{\mathbb R},d\omega)$ 内の観測量 ${\mathsf O} := (X_{\mathbb R},{\cal F}_{X_{\mathbb R}},F)$ を考える。 混合言語ルール$^{\mbox{(m)}}$ 1 ($\S$9.1) に従えば、次が言える。

注意17.2 上で、次が気になるかもしれない：

注意17.3 分散$\sigma_i^2$ を次のように定義しよう。 \begin{align} \sigma_i^2 := \int_{\Omega_{\mathbb R}} (\omega-\mu_i)^2 \, [\Phi_\ast(1_{\theta_i})](\omega) \, d\omega \quad (i=1,2,\dots,n), \tag{17.1} \end{align} ここで、$\mu_i$ は分布$\Phi_\ast(1_{\theta_i})$の期待値で、 \begin{align} \mu_i := \int_{\Omega_{\mathbb R}} \omega \, [\Phi_\ast(1_{\theta_i})](\omega) \, d\omega \quad (i=1,2,\dots,n). \tag{17.2} \end{align} とする。 本章では、 $\sigma_i^2$ は$\theta_i$に依存しないとは 仮定しない。

上では、 ある生徒$\theta_i \;(\in \Theta)$に対するテストを考えたが、 次に、 クラス(生徒のグループ)$\Theta (=\{\theta_1, \theta_2, ..., \theta_n \})$ に対するテストを議論しよう。 上と同様に、 $ \Omega_{\mathbb R}^n={\mathbb R}^n $ として、 $n$次元ルベーグ測度空間 $(\Omega_{\mathbb R}^n,{\cal F}_{\Omega_{\mathbb R}^n},d\omega^n)$を考える。 さらに、同様に、観測量${\mathsf O} := (X_{\mathbb R},{\cal F}_{X_{\mathbb R}},F)$ の混合測定${\mathsf M}_{L^\infty(\Omega_{\mathbb R},d\omega)}({\mathsf O},$ $ S_{[\ast]}(\Phi_\ast(1_{\theta_i})))$ ($i=1,2,\dots,n$)を考えよう。 したがって、$L^\infty(\Omega_{\mathbb R}^n,d\omega^n)$内の並行測定${\mathsf M}_{L^\infty(\Omega_{\mathbb R}^n,d\omega^n)} (\widehat{\mathsf O}, S_{[\ast]}(\widehat{\rho}))$ where $\widehat{\mathsf O} := (X_{\mathbb R}^n,{\cal F}_{X_{\mathbb R}^n},\widehat{F})$を得る。 すなわち、 \begin{align*} [\widehat F (\Xi_1 \times \Xi_2 \times \cdots \times \Xi_n)](\omega_1,\omega_2,\dots,\omega_n) = [F(\Xi_1)](\omega_1) \cdot [F(\Xi_2)](\omega_2) \cdots [F(\Xi_n)](\omega_n), \end{align*} で、 \begin{align*} \widehat{\rho} (\omega_1,\omega_2,\dots,\omega_n) = [\Phi_\ast(1_{\theta_1})](\omega_1) \cdot [\Phi_\ast(1_{\theta_2})](\omega_2) \cdots [\Phi_\ast(1_{\theta_n})](\omega_n), \end{align*} よって、並行測定${\mathsf M}_{L^\infty(\Omega_{\mathbb R}^n,d\omega^n)} (\widehat{\mathsf O}, S_{[\ast]}(\widehat \rho))$は次のように定義できる： \begin{align*} \otimes_{\theta_i \in \Theta} {\mathsf M}_{L^\infty(\Omega_{\mathbb R},d\omega)}({\mathsf O}, S_{[\ast]}(\Phi_\ast(1_{\theta_i}))). \end{align*} ここで、以下のようなテンソル積を使った。 \begin{align*} \otimes_{k=1}^n L^\infty(\Omega_{\mathbb R},d\omega) = L^\infty(\Omega_{\mathbb R}^n,d\omega^n) \quad \text{and} \quad \otimes_{k=1}^n L^1(\Omega_{\mathbb R},d\omega) = L^1(\Omega_{\mathbb R}^n ,d\omega^n). \end{align*} 次の定義から始める。

各生徒$\theta_i \;(\in \Theta)$に対するテスト観測量の測定$ {\mathsf M}_{L^\infty(\Omega_{\mathbb R},d\omega)}({\mathsf O}_\tau, S_{[\ast]}(\Phi_\ast(1_{\theta_i}))) $ を略して、 ${\mathsf M}_{{\mathsf O}_\tau}^{(i)}$と記す。 すなわち、 \begin{align} {\mathsf M}_{{\mathsf O}_\tau}^{(i)} := {\mathsf M}_{L^\infty(\Omega_{\mathbb R},d\omega)}({\mathsf O}_\tau, S_{[\ast]}(\Phi_\ast(1_{\theta_i}))). \tag{17.4} \end{align} とする。

ここに, $(X_{\mathbb R}, {\cal F}_{X_{\mathbb R}}, P_i)$は、測定 ${\mathsf M}_{{\mathsf O}_\tau}^{(i)}$のサンプル空間である。

ここで、$W: X_{\mathbb R}^n \to {\mathbb R}$を統計量(すなわち、可測関数)として、 その期待値${\cal E}_{{\mathsf M}_{{\mathsf O}_\tau}^\otimes}[W]$を 次のように定める：

定義17.6 $L^\infty(\Omega_{\mathbb R},d\omega)$内の テスト観測量${\mathsf O}_\tau := (X_{\mathbb R},{\cal F}_{X_{\mathbb R}},F_\tau)$を考える。
(i: 生徒$\theta_i$の得点) 生徒$\theta_i \;(\in \Theta)$に対するテスト ${\mathsf M}_{L^\infty(\Omega_{\mathbb R},d\omega)}({\mathsf O}_\tau, S_{[\ast]}(\Phi_\ast(1_{\theta_i})))$ (or in short, ${\mathsf M}_{{\mathsf O}_\tau}^{(i)}$)を考える。 その得点の期待値、分散は次のように定める。

グループテスト$\otimes_{\theta_i \in \Theta} {\mathsf M}_{L^\infty(\Omega_{\mathbb R},d\omega)}({\mathsf O}_\tau, S_{[\ast]}(\Phi_\ast(1_{\theta_i})))$ (or in short, ${\mathsf M}_{{\mathsf O}_\tau}^\otimes$)の測定値を $(x_1, x_2, ..., x_n )$とする。 このとき、期待値 $\frac1n (x_1+x_2+\cdots+x_n)$ と分散を次のように定める。

ここに、${\mathsf O}_E := (X_{\mathbb R},{\cal F}_{X_{\mathbb R}},E)$は$L^\infty(\Omega_{\mathbb R},d\omega)$内の精密観測量。