たとえば、次のような「確率」が意味を持つのだろうか? または、統一的に議論できるだろうか?
$(A1):$ 日本が、次のFIFAワールドカップで優勝する確率 $(A2):$ 明日雨になる確率 $(A3):$ 源義経がジンギスカンになった確率 $(A4):$ サイコロを投げて3の目がでる確率 $(A5):$ 二人でジャンケンをしたとき相手がパーを出す確率
また、「等確率の原理」を正当化できるのだろうか?
ここで、「等確率の原理」とは次の習慣のことである:
たとえば、
と考える習慣のことを
「等確率の原理」と言う。
$(B):$
今可能な状況が$A_1$, $A_2$,...,$A_n$と$n$個あるとして、どれが起このか積極的な理由を知らないときに、
いずれの状況も確率$1/n$で起こる
この節では、 第9章で述べた次の混合測定の枠組みの中で、 すなわち、 \[ \underset{\mbox{ (=量子言語)}}{\fbox{混合測定理論 (A)}} := \underbrace{ \textcolor{red}{ \underset{\mbox{ (\(\S\)9.1)}}{ \overset{ [\mbox{ (混合) 言語ルール1}] }{\fbox{混合測定}} } } \quad + \quad \underset{\mbox{ ( \(\S \)10.3)}}{ \overset{ [{\mbox{ 言語ルール2}}] }{\fbox{因果関係}} } }_{\mbox{ 一種の呪文 (アプリオリな総合判断)}} + \underbrace{ \underset{\mbox{ (\(\S\)3.1) }} { \overset{ {}}{\fbox{言語的解釈}} } }_{\mbox{ 呪文の使い方のマニュアル}} \tag{9.2} \] の枠組みの中で、 上の二つの(A)と(B)に答える。
18.1.1:簡単な例; 量子言語で「確信・信念」を記述できるか?
次の簡単な例(問題9.4の 復習 ) から始めよう。
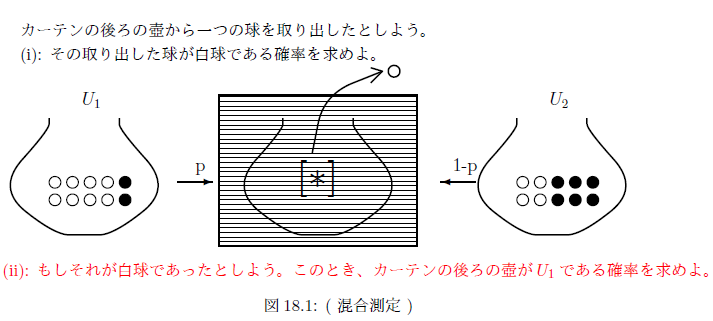
| $(C):$ | あなたは、カーテンの後ろの壺が$U_1$か$U_2$かどうかは 知らないが、その「確率」が$p$と$1-p$であることは知っている。 |
解答 18.2 (=解答 9.13)
離散距離空間 $\Omega=\{ \omega_1, \omega_2 \}$ に 個数測度$\nu_c$を仮定する。 したがって、 $C_0(\Omega)$ $=C(\Omega )$ $= L^\infty (\Omega, \nu_c )$ と考えてよい。 $C(\Omega)$内の 二つの観測量 ${\mathsf O} = ({} \{ {{{W}},} {{B}} \},$ $ 2^{\{ {{W}}, {{B}} \} } ,$ $ F{})$ と ${\mathsf O}_U = ({} \{ {{{U_1}},} {{U_2}} \},$ $ 2^{\{ {{U_1}}, {{U_2}} \} } ,$ $ G_U{})$ を次のように定める: \begin{align*} & F({}\{ {{W}} \}{})(\omega_1{})= 0.8, F({}\{ {{B}} \}{})(\omega_1{})= 0.2, F({}\{ {{W}} \}{})(\omega_2{})= 0.4, F({}\{ {{B}} \}{})(\omega_2{})= 0.6 \\ \\ & G_U({}\{ {{U_1}} \}{})(\omega_1{})= 1,% G_U({}\{ {{U_2}} \}{})(\omega_1{})= 0,% G_U({}\{ {{U_1}} \}{})(\omega_2{})= 0,% G_U({}\{ {{U_2}} \}{})(\omega_2{})= 1 \end{align*}
こkで、"$W$"と"$B$" はそれぞれ"白" と "黒"を意味する。 同一視 $U_1 \approx \omega_1$ と $U_2 \approx \omega_2$ の下に、 上の状況を表す混合状態 $\rho^{(p)}_{\mbox{prior}} ( \in {\mathcal M}_{+1} (\Omega))$ は次のようになる: \begin{align*} \rho^{(p)}_{\mbox{ prior}} = p \delta_{\omega_1} + (1-p) \delta_{\omega_2} \end{align*} ここに$\delta_{\omega}$は 点$\omega$における点測度とする。 したがって、次の混合測定を考えればよい。 \begin{align} & {\mathsf M}_{C (\Omega)}({\mathsf O} \times {\mathsf O}_{U} := ({} \{ {{{W}},} {{B}} \} \times \{U_1, U_2\} ,2^{ \{ {{{W}},} {{B}} \} \times \{U_1, U_2\} } , F \times G_U{}), S_{[*]}( \rho^{(p)}_{\mbox{ prior}} )) \\ & \tag{18.2} \end{align}
混合言語ルール$^{\mbox{(m)}}$ 1 ($\S$9.1)に従えば、問題18.1の(i)の解答は、以下のようになる:
| $(D):$ | 混合測定 ${\mathsf M}_{C (\Omega)}({\mathsf O} \times {\mathsf O}_{U}, S_{[*]}( \rho^{(p)}_{\mbox{ prior}} ))$ によって得られる測定値 $(x,y)$が $\{W \} \times \{U_1, U_2 \}$ に属する確率は、 次で与えられる: \begin{align*} {}_{{\mathcal M}(\Omega)}(\rho^{(p)}_{\mbox{ prior}}, F(\{W\}) )_{C_{}(\Omega )} = 0.8 p + 0.4 (1-p). \end{align*} |
さらに、白球を取り出したと仮定しよう。 このときは解答9.13 (=ベイズの定理 ) によって、測定後の 新しい混合状態$\rho^{(p)}_{\mbox{ post}} (\in {\mathcal M}_{+1}(\Omega ))$ は以下のようになる: \begin{align} \rho^{(p)}_{\mbox{ post}} & % = \frac{ F({}\{ {{W}}\} {}) \rho^{(p)}_{\mbox{ prior}} }{\int_\Omega [F( \{ {{W}}\} )](\omega) \rho^{(p)}_{\mbox{ prior}}(d \omega )} = \frac{\displaystyle 0.8 p }{\displaystyle 0.8p+0.4(1-p) } \delta_{\omega_1} + \frac{\displaystyle 0.4(1- p) }{\displaystyle 0.8p+0.4(1-p) } \delta_{\omega_2} \\ & \tag{18.3} \end{align} したがって、 問題(ii)の解答は次のようになる: \begin{align*} {}_{{\mathcal M}(\Omega)}(\rho^{(p)}_{\mbox{ post}}, G_U(\{ U_1 \}) )_{C_{}(\Omega )} = \frac{\displaystyle 0.8 p }{\displaystyle 0.8p+0.4(1-p) } \end{align*}
問題18.1
(簡単のため,
$
p=1/4, \;\; 1-p = 3/4
$
と置く
)を参考にして、以下のようにな議論をする。
100人の集団を考えよう。
次の状況(E)を想定する。
100人のうち、
\begin{align*}
\mbox{(E)}
\;
\begin{cases}
\text{「$[\ast]= U_1$
(i.e.,カーテンの後ろの壺は
$U_1$)」と25人が信じている(投票する)
}
\\
\text{「$[\ast]= U_2$
(i.e.,カーテンの後ろの壺は
$U_2$)」と75人が信じている(投票する)
}
\end{cases}
\end{align*}
この状況を以下のように図示しておく
(図18.1):
ここで、次の問題を考察する:
問題18.3 状況(E)と状況(C) ( $ p=1/4, \;\; 1-p = 3/4 $ ) を比較しよう。 さて、次の問題を考える。
| $(F_1):$ | 確信 [状況(E)]を 確率 [状況(C)]のように理解できるか? |
| $(F_2):$ | 確信 [状況(E)]は、混合測定 (i.e., 混合言語ルール$^{\mbox{(m)}}$ 1 ($\S$9.1) ) で、 したがって、量子言語で記述できるか? |
18.1.2: 問題18.3への肯定的解答
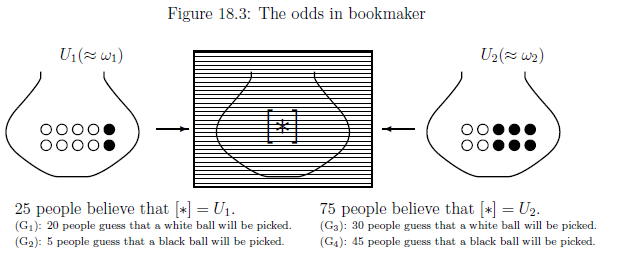
100人は、 図18.2 の状況を把握しているので、 次の(G)(=図18.3)を仮定するのは自然である。
| $(G):$ | $ \begin{cases} \text{25人が「$[\ast]= U_1$」を信じる} \\ \quad \Longrightarrow \begin{cases} \text{(G$_1$):20人が「白球が取り出される」方に賭ける } \\ \text{(G$_2$): 5人が「黒球が取り出される」方に賭ける } \end{cases} \\ \text{75人が「$[\ast]= U_2$」を信じる} \\ \quad \Longrightarrow \begin{cases} \text{(G$_3$):30人が「白球が取り出される」方に賭ける } \\ \text{(G$_4$): 45人が「黒球が取り出される」方に賭ける } \end{cases} \end{cases} $ |
さて、
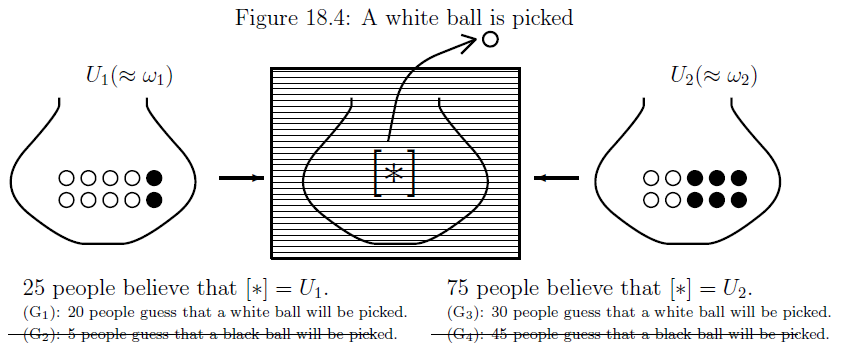
| $\bullet$ | 上図で、白玉が得られたとしよう。 すなわち、次図の状況を想定しよう |
このときは、上の (G$_2$)と(G$_4$)は、賭けに負けたことになる。 したがって、
となり、結局、次の最終図をえる。
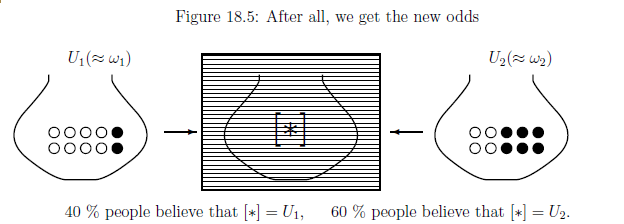
したがって、次を得る。 \begin{align} \overset{{\mbox{ (事前状態)}}}{\underset{\frac{1}{4} \delta_{\omega_1} + \frac{3}{4} \delta_{\omega_2}}{\fbox{ 図18.3}}} \xrightarrow[{\mbox{$\qquad \qquad$}}]{} \overset{{\mbox{(白球が取り出された)}}}{\fbox{図18.4}} \xrightarrow[{\mbox{$\qquad \qquad$}}]{} \overset{{\mbox{(事後状態)}}}{\underset{\frac{2}{5} \delta_{\omega_1} + \frac{3}{5} \delta_{\omega_2}}{\fbox{ 図18.5}}} \tag{18.4} \end{align}
次の混合測定 (i.e., 式(18.2) ($p=1/4$, $1-p=3/4$) ):
\begin{align} & (18.2) = {\mathsf M}_{C_{} (\Omega)}({\mathsf O} \times{\mathsf O}_U = ({} \{ {{{W}},} {{B}} \} \times \{U_1, U_2\},2^{ \{ {{{W}},} {{B}} \} \times \{U_1, U_2\} } , F\times G_U{}) , S_{[*]}( \rho^{(1/4)}_{\mbox{prior}} )) \\ & \tag{18.5} \end{align} を考えたとき、 上の(18.4)式は、 ベイズの結果 (18.3) と等しいことに注意せよ。ここで、次の(H)を考える:
| $(H):$ |
100人の中から一人を無作為に選び、彼/彼女に次のように質問する:
|
この(H)と測定(18.5)と同一視できることを、以下に示そう: 状態空間$\Theta=\{ \theta_1, \theta_2, ..., \theta_{100} \}$を設定して、基本構造 \begin{align*} C(\Theta) \subseteq L^\infty(\Theta ) \subseteq B(L^2(\Theta )) \end{align*} を考えよう。 $C(\Theta)$内の 観測量 $\widehat{\mathsf O}= ( \{W,B \}, 2^{\{W,B \} },$ $ \widehat{F})$ と $\widehat{\mathsf O}_{U}= ( \{U_1, U_2 \}, 2^{\{U_1, U_2 \} }, \widehat{G}_U)$ を次のように定める。 \begin{align} & [\widehat{F} (\{W\})](\theta_k)=4/5,\;\; [\widehat{F}(\{B\})](\theta_k)=1/5, \;\; (k=1,2,...,25) \nonumber \\ & [\widehat{F}(\{W\})](\theta_k)=2/5,\;\; [\widehat{F}(\{B\})](\theta_k)=3/5, \;\; (k=26,27,...,100) \tag{18.6} \\ & [\widehat{G}_{U}(\{ U_1 \})](\theta_k)=1,\;\; [\widehat{G}_{U}(\{ U_2 \})](\theta_k)=0, \;\; (k=1,2,...,25) \nonumber \\ & [\widehat{G}_{U}(\{ U_1 \})](\theta_k)=0,\;\; [\widehat{G}_{U}(\{ U_2 \})](\theta_k)=1, \;\; (k=26,27,...,100) \tag{18.7} \end{align} この 同時観測量 を $ \widehat{\mathsf O} \times \widehat{\mathsf O}_{U} $ とする。 ここで、
- 混合状態$\nu_0(\in {\mathcal M}_{+1}(\Theta))$を $\nu_0= (1/100) \sum_{k=1}^{100} \delta_{\theta_k} (\in {\mathcal M}_{+1}(\Theta))$
のように定める。 この決定因果作用素 $\Phi:C(\Omega) \to C(\Theta)$の下に、 測定(18.8)は 測定(18.5)と同一視できる: すなわち、
\begin{align*} \underset{\mbox{}}{ \fbox{(H)=(18.8): ハイゼンベルグ描像} } \xleftarrow[\mbox{同一視}]{\Phi} \underset{\mbox{}}{ \fbox{(18.5): シュレーディンガー描像} } \end{align*} よって、問題18.3に肯定的に答えることができた。| $(I_1):$ | 確信 [状況(E)]を 確率 [状況(C)]のように理解できる. |
| $(I_2):$ | 確信 [状況(E)]は、 「100人の中から無作為に一人を選ぶ」という解釈を添付して、 混合測定 (i.e., 混合言語ルール$^{\mbox{(m)}}$ 1 ($\S$9.1) ) で、 したがって、量子言語で記述できる。 |
この節の、最初の問い掛け(A):
| $(A)$ | 日本が、次のFIFAワールドカップで優勝する確率 |