次の公準を主張する。

公準18.4 [等確率の原理(=等重率)] 有限状態空間 $\Omega=\{\omega_1,\omega_2,\ldots,$ $\omega_n\}$ (離散距離空間) を考える。 ${\mathsf O}=(X, {\cal F}, F)$ を $C_{} (\Omega)$内の観測量 とする。 ここで、 測定 $ {\mathsf M}_{C_{} (\Omega )}({\mathsf O} , S_{[ \ast]} ) $ は、混合測定 $ {\mathsf M}_{C_{} (\Omega )}({\mathsf O} , S_{[ \ast]}(\rho_{\mbox{e} }) ) $ によって代用できると考えることも一理ある。 ここで、 \begin{align} \rho_{\mbox{ e}} = \frac{1}{n} \sum_{k=1}^n \delta_{\omega_k} \tag{18.9} \end{align}

説明 各$\omega_k \in $$\{\omega_1,\omega_2,\ldots,$ $\omega_n\}$に取り立てた差異がないときは、 賭けと考えれば, 誰もが、 一番人気のない状態 (たとえば、 $\omega_{k_0} \in \Omega$ ) を選ぶだろう。 したがって、人気の分布は一様分布(18.9)になると 考えることは自然である。 前節で述べたように、 人気・信念を混合測定 $ {\mathsf M}_{C_{} (\Omega )}({\mathsf O} , S_{[ \ast]}(\rho_{\mbox{e}}) ) $ と特徴つけできる。 混合測定 $ {\mathsf M}_{C_{} (\Omega )}({\mathsf O} , S_{[ \ast]}(\rho_{\mbox{ e} }) ) $ は測定 $ {\mathsf M}_{C_{} (\Omega )}({\mathsf O} , S_{[ \ast]} ) $ の代用として使える。 念を押すと、

$(J):$ 言語ルール　1 (or 言語ルール$^{(m)}$　1 ) の文脈の中で整合性があえば、 「確率」という言葉は自由に使える
したがって、 等確率の原理(B)、 再掲すると、

$(B):$ 今可能な状況が$A_1$, $A_2$,...,$A_n$と$n$個あるとして、どれが起このか積極的な理由を知らないときに、 いずれの状況も確率$1/n$で起こると考える習慣
には理がある。
$\square \quad$


現在においても、等重率の正統性がまだ承認されていない歴史があるとしたら、 上の(J)が未だ常識化されていないことに起因すると考える。

$\fbox{注釈18.1}$ さて、
$(\sharp):$ 本書では、三種類の「等確率の原理(=等重率)」を扱った。 すなわち、
$(\sharp_1):$ 定理5.19の等確率の原理(cf. $\S$5.6)
$(\sharp_2):$ 定理9.18の等確率の原理(cf. $\S$9.7)
$(\sharp_3):$ 公準18.4の等確率の原理(cf. $\S$18.2)
である。

二つの等確率の原理 (($\sharp_2$) と($\sharp_3$)) の理解を深めるために、 次の問題18.5 を補足しておく。 この問題と 問題5.14(cf. $\S$5.5) と 問題9.17(cf. $\S$9.7) とを比較検討してもらいたい。

問題18.5 [モンティホール問題; 問題5.14 ;等重率]
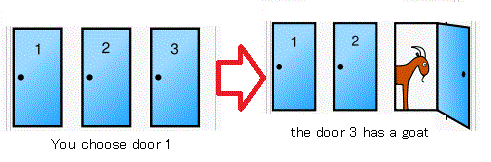
$\quad$ あなたはゲームショーに出演している． 3つのドア (すなわち，「1番」， 「2番」， 「3番」 ) のうちの 1つのドアの後ろには{自動車(当り)}, 他の2つのドアの後ろには 羊(はずれ)が隠されている． 司会者は，どのドアの後ろに自動車が隠されているかを知っている． しかし， あなたはそれを知らない． 司会者は問う「どのドアの後ろが自動車だと思いますか？」

さて，あなたはあるドアを選んだと仮定する． たとえば, 1番のドアを選んだとする． このとき， 司会者が 「実は，3番ドアの後ろは羊です」 と言う． 更に，司会者は問う． 「あなたは1番のドアを選んでしまいましたが， 今からでも変更可能ですよ． 2番のドア に変更しますか？ 」と． さて，あなたはどうするか？


  • Figure 18.6: モンティホール問題


解答

公準18.4 より、 測定 $ {\mathsf M}_{C_{} (\Omega )}({\mathsf O} , S_{[ \ast]} ) $ は、混合測定 $ {\mathsf M}_{C_{} (\Omega )}({\mathsf O} , S_{[ \ast]}(\rho_{\mbox{ prior} }) ) $ によって代用しても良いのだから、 問題5.14 (フィッシャーの最尤法) を 問題9.16 (ベイズの方法) に帰着できて、問題9.16の解答に従えばよい。

$\square \quad$