$(C_1)$
$
\underset{\mbox{ (=�ʎq����)}}{\fbox{�������藝�_ (A)}}
:=
\underbrace{
\underset{\mbox{ (\(\S\)2.7)}}{
\overset{
[\mbox{ (����) ���ꃋ�[��1}]
}{\fbox{��������}}
}
\quad + \quad
\underset{\mbox{ ( \(\S \)10.3)}}{
\overset{
[{\mbox{ ���ꃋ�[��2}}]
}{\fbox{���ʊW}}
}
}_{\mbox{ ���̎��� (�A�v���I���ȑ������f)}}
+
\underbrace{
\underset{\mbox{
(\(\S\)3.1)
}}
{
\overset{
{}}{\fbox{����I����}}
}
}_{\mbox{ �����̎g�����̃}�j���A��}}
$
$(C_2)$
$
\underset{\mbox{ (=�ʎq����)}}{\fbox{�������藝�_ (A)}}
:=
\underbrace{
\color{red}{
\underset{\mbox{ (\(\S\)9.1)}}{
\overset{
[\mbox{ (����) ���ꃋ�[��1}]
}{\fbox{��������}}
}
}
\quad + \quad
\underset{\mbox{ ( \(\S \)10.3)}}{
\overset{
[{\mbox{ ���ꃋ�[��2}}]
}{\fbox{���ʊW}}
}
}_{\mbox{ ���̎��� (�A�v���I���ȑ������f)}}
+
\underbrace{
\underset{\mbox{
(\(\S\)3.1)
}}
{
\overset{
{}}{\fbox{����I����}}
}
}_{\mbox{ �����̎g�����̃}�j���A��}}
$
19.2.1: �ʎq����̑S�̑�
���̓����,�ȉ��̂悤�ɂȂ�.
$(B):$
$
\underset{(=\mbox{ �ʎq����})}{\mbox{���藝�_}}
\left\{\begin{array}{ll}
\underset{\mbox{($\sharp_1$)}}{
\mbox{�����n}}
\left\{\begin{array}{ll}
\!\!
\mbox{�ÓT�V�X�e��}
:
\mbox{ �t�B�b�V���[���v�w}
\\
\!\!
\mbox{ �ʎq�V�X�e��}
:
\mbox{
�ʏ�̗ʎq�͊w
}
\\
\end{array}\right.
\\
\\
\underset{\mbox{($\sharp_2$)}}
{\mbox{�����n}}
\left\{\begin{array}{ll}
\!\!
\mbox{ �ÓT�V�X�e��}
:
\mbox{�x�C�Y���v�w, }\\
\qquad \qquad \mbox{�J���}���t�B���^}
\\
\!\!
\mbox{ �ʎq�V�X�e��}
:
\mbox{ �ʎq�f�R�q�[�����X
}
\\
\end{array}\right.
\end{array}\right.
$
������,���ꃋ�[��1��2�͕K�v�s���ł��邪,
����I����(���ꃋ�[��1��2�̎g�����}�j���A��)�̐�����,����($E_1$)��($E_2$)�̂���������ł���.
$(E_1):$
���ꃋ�[��1��2�����s����Ŏg�������Ă����,
����I���߂͎��R�ɉ�ł�����̂�,�Ƃ肽�ĂĖ{���ŏ����K�v���Ȃ�����

$\qquad \qquad \qquad $���E�L�q�j�̐}��
$(E_2):$
�{���̓}�j���A���{(�N�b�N�u�b�N)�ł�����,�{���ŏ��������ׂĂ�����I���߂ł���.�Ƃ͌����Ă�,���ɏd�v�Ȃ̂�,
�ł���.
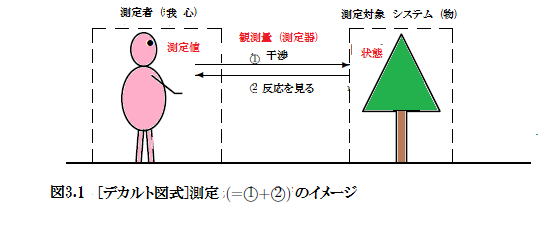
�}��19.1(�E�})�̇H��M����Ȃ�A�m���_�̊�{���_�u�m����Ԃ͈�����v���A�ʎq����́u�����,����v�Ɉ����p�����ƍl����͎̂��R�Ǝv���B
�܂�,
���Ƃ͕K�R�Ǝv��.
$(E_3):$
�N�w�̖{��(�_�I�ϔO�_)�̌n��(�E�̐}��19.1�̇@---�E---�G)�̓��B�_���ʎq����Ƃ����咣�Ȃ̂�����,
�M���V���ȗ��̓N�w�҂̋����̑�����,����I���߂̈ꕔ���\�����Ă���
19.2.2 �ʎq����̓���
�ʎq����͎��̓��������F
�ʎq����̓���
$(F_1):$
�m���E���A���e�B(�`����w):
�ʎq�����,�u���߂Ɍ��t���肫�v�̐��_��
����I�Ȋw�ςɏ������Ă���`����w�ł���.
����������,�ʎq����̂��ׂĂ��u�v�Z�ׂ̈̓���v�ł���.
$(F_2):$
����ɂ��g�����̎��k�͂Ȃ�:
�u����͈���v�Ȃ̂�,�����̏ɂ��Ă̏��邱�Ƃ��ł��Ȃ�.
����������,�����̂��Ƃ͈�؉�������Ȃ�.
�u(�G��E�f����ςĂ���悤�Ȃ��̂�)�ϋq�͕���ɏオ��Ȃ��v�̂�����A
�g�����̎��k�͈Ӗ��������Ȃ��B
�������Ȃ���A
"�ˉe���� 11.6 ( in Section 11 )"�̈Ӗ��ŁA"�g���̎��k"��ʎq����ŋL�q�ł���B
$(F_3):$
�B�ꂽ�ϐ��̔�d�v��:
�B�ꂽ�ϐ��̖��ӎ����̂��d�v�Ƃ����킯�ł͂Ȃ�.
�Ƃ������́A
��X�́A�u�ʎq�͊w�ɂ�,�{���̖��͑��݂��Ȃ��v�ƌ��_�����̂�����A
�B�ꂽ�ϐ��ɂ��ĉ������y�ł��Ȃ��B
���������A�u�B�ꂽ�ϐ��v�̈Ӗ����疾�m�ł͂Ȃ����A����m������K�v���Ȃ���
�l����B
$(F_4):$
��I:
�ÓT�n�̓��I�V�X�e�����_�ł́A
��I�ߒ�(=�}���R�t�ߒ�)���l���邱�Ƃ́A���ʂł���B
����āA�ʎq����ɂ����Ă��A
����I���ʍ�p�f�����łȂ���,
�}���R�t���ʍ�p�f���l����.
����������,�V�����[�f�B���K�[�������Ƃ��j���[�g�������������łȂ��ʎq�f�R�q�[�f�����X�Ƃ��g�U�������������B
����ɂ��ʎq����̋L�q�͂����債��,�ʎq����Łu�V�����[�f�B���K�[�̔L�v�̋L�q���\�ɂȂ�.

$(F_5):$
����҂̖���:
�ʎq����́C[�����]��[���肳������]�̓�ō\�������_�I����ł���.
���������āC���ۂ͈ꌳ�I�ł��邪�C������L�q���錾��͓_�I�ɂȂ�D�Ⴆ�Č����Ȃ�A��l�̏����E���M�@�@(������鏬���E���M)�ł��邪�A�����o��l���ł����Ă͂Ȃ�Ȃ�(�ϋq�͕���ɏオ��Ȃ�)�B�܂��́A�u�G��E�f��̊��z�����v�Ǝv���悢�B
$(F_6):$
�p���h�b�N�X�E���������̉���:
�����̃p���h�b�N�X�E��������肪�������ꂽ�B
$(a)$
�L�q���錾�ꂪ�����������Ƃɂ��p���h�b�N�X�F
�m��, ���ʊW�A����Ƃ͉����H�@�[�m���̃p���h�b�N�X�A���d���A�ÓT�O�i�_�@

$(b)$
�L�q�͂����債�����Ƃʼn��������p���h�b�N�X�F
�V�����[�f�B���K�[�̔L�A
$(c)$
�L�q�͂����m�����ꂽ���Ƃʼn��������p���h�b�N�X(��蓾�ʂ��Ƃ́A���ق��Ȃ���Ȃ�Ȃ�)�F
�E�B�O�i�[�̗F�l�A�x���I�������A(�K���}���������ɂ��)�n�C�[���x���O�̕s�m�萫����
$(d)$
���ʂ����ǂ��Ȃ������ƂŖ��m�����ꂽ���ƁF
���v�w�̏����(�Ŗޖ@�A�x�C�Y�̕��@�A�������̓���(�M����ԁA��������AANOVA), ��A���́A�J���}���t�B���^)
$(F_7):$
��Ǐ����E������:
���u��p(= ��Ǐ����E������)��F�߂�. ���ꂪ,�B��̃p���h�b�N�X�ł���.
19.2: �v��(�ʎq����)
This web-site is the html version of "Linguistic Copehagen interpretation of quantum mechanics; Quantum language [Ver. 4]" (by Shiro Ishikawa; [home page] )
PDF download : KSTS/RR-18/002 (Research Report in Dept. Math, Keio Univ. 2018, 464 pages)
�@
�@�@
���藝�_
(= �ʎq���� )
�͈ȉ��̂悤��,���ނł���
