偙偺儁乕僕偩偗偱丄検巕尵岅(=應掕棟榑)偺偡傋偰偑傢偐傞
忋偺尵岅揑僐儁儞僴乕僎儞夝庍$(B_1) \sim (B_7)$偼偡傋偰乽偄偐偑傢偟偄乿偲巚偆偐傕偟傟側偄丅丂挊幰偼丄幚偼丄
偩偲巚偭偰偄傞丅偟偐偟丄検巕椡妛偺僐儁儞僴乕僎儞夝庍偼暔棟妛側偺偩偐傜丄偁傑傝儊僠儍僋僠儍側偙偲偼尵偊側偄丅
暔棟妛撪偺庡挘偩偲偟偨傜$(B_1) \sim (B_7)$偺偳傟傕庴偗擖傟偑偨偄偐傜偱丄丂
懡彮偺儃僇僔(傗曄宍丒柪嵤)傪巤偟偰乽検巕椡妛偺僐儁儞僴乕僎儞夝庍乿偼捠忢偼採帵偝傟偰偄傞偺偩偑丄偦偺儃僇僔偵傛偭偰偝傜偵暘偐傝偵偔偟偰偄傞
偲傕尵偊傞丅丂偟偐偟丄検巕尵岅偺尵岅揑僐儁儞僴乕僎儞夝庍偺応崌偼丄
忋偱弎傋偨傛偆偵丄丂偙傟傪幃(1)偺傛偆偵暔棟壔偡傞偲, 僥僋僯僢僋$(B_1) \sim (B_7)$傪暔棟尰徾偲尒傞偙偲偵側傝,
乽(暔棟揑偵)偄偐偑傢偟偄乿偙偲偵側傞偑丄
偙傟偑乽(暔棟妛偺)検巕椡妛偺夝庍栤戣乿偑偄偮傕僋儗乕僕乕側尨場偲峫偊傞丅
偡側傢偪丄検巕尵岅偼
§1.摴嬶庡媊偲偟偰傕検巕尵岅
摴嬶庡媊偲偼丄丂尰徾偺攚屻偵偁傞幚嵼偺恀偺巔傪捛媶偡傞偙偲傪偟側偄偱丄壢妛棟榑傪尰徾傪婰弎偡傞偨傔偺尵岅( 偲偐慻怐壔丒梊應偡傞偨傔偺宍幃揑側摴嬶丒憰抲)偱偁傞偲尒側偡棫応偱偁傞丅丂検巕椡妛偺応崌偼丄R. 僼傽僀儞儅儞(検巕揹帴婥妛偺憂巒幰偵堦恖)偺桳柤側尵梩丗
乽偦偙丄丂怺偔峫偊偨傜傾僇儞乿
傪拤幚偵幚峴偡傟偽丄乽摴嬶庡媊偲偟偰偺検巕椡妛乿偑摼傜傟傞丅丂挊幰偼丄偙傟偑乽検巕椡妛偺僐儁儞僴乕僎儞夝庍乿偺堦偮偺懁柺偱偁傞偲峫偊丄乽摴嬶庡媊偲偟偰偺検巕椡妛乿傪
偲柤晅偗偨丅摴嬶庡媊偼丄棟榑偺桪楎偑偦偺桳梡惈偵傛偭偰寛傑傞偲峫偊傞偺偱丄検巕椡妛傪桳梡側傛偆偵嶌傝曄偊偰丄偦偺寢壥偲偟偰弌棃忋偑偭偨棟榑偑暔棟妛偱側偔側偭偰傕椙偟偲偡傞丅丂帠幚丄乽検巕尵岅乿偼暔棟妛(宍帶壓妛[=幚尡偵傛偭偰敀崟偮偗傞偙偲偑偱偒傞妛栤])偱側偔偰丄尵岅(宍帶忋妛[=宍帶壓妛偺懳媊岅])偵側傞丅
§2.悽奅婰弎巎偺拞偱偺検巕尵岅
寢榑傪愭偵弎傋傞偲丄悽奅婰弎巎偺拞偱偺"検巕尵岅"偺埵抲偼壓恾偺傛偆偵側傞丅

忋偱丄幚嵼揑壢妛娤偼暔棟妛偲巚偊偽傛偄丅丂尵岅揑壢妛娤偼埲壓偱愢柧偡傞丅
尵岅揑夝庍偼丄僜僔儏乕儖傗僂傿僩僎儞僔儏僞僀儞摍偵傛偭偰側偝傟偨乽嘐偺揮夞乿(尵岅榑揑揮夞: 擣幆偐傜尵岅傊偺揮夞)偵戝偒側塭嬁傪庴偗偰偄傞丅丂幚嵼揑偱偼側偔丄擣幆揑偱傕側偔偰丄尵岅揑偱偁傞丅
忋恾(i.e., ⑦--⑨)偐傜丄 "検巕尵岅"偼師偺摿挜傪帩偮丗
§3.挊幰偺婅朷: 乽弶傔偵検巕尵岅偁傝偒乿偱乽検巕椡妛亖検巕椡妛偺暔棟壔乿偲巚偄偨偄
乽桞堦偺椙偄宍帶忋妛偼悢妛偱偁傞乿偼働儖償傿儞嫧偺尵梩偱偁傞偑丄揘妛偺挏棊偑業傢偵側偭偨崱擔偱偼丄旕忢偵愢摼椡偺偁傞尵梩偱扤傕偑擺摼偟偰偟傑偆偐傕偟傟側偄丅丂悢妛埲奜偺宍帶忋妛偵偼丄乽偄偐偑傢偟偝乿傗乽僋儗乕僕乕偝乿偑晅偒傑偲偆偲峫偊傞偐傕偟傟側偄丅
偦偆偩偲偟偰傕丄検巕椡妛偺夝庍(僐儁儞僴乕僎儞夝庍丄懡悽奅夝庍丄儃乕儉偺旕嬊強揑塀傟偨曄悢夝庍摍)傕偙偲偛偲偔僋儗乕僕乕側偺偩偐傜丄
検巕尵岅偲憡惈偑僺僢僞儕偲崌偭偰偄傞偐傕偟傟側偄丅
偝偰丄
偲偐丄
偵埲壓偺傛偆偵摎偊偨偄丅
挊幰偑婅朷偡傞僗僩乕儕乕偼師偺[$(A_1)+(A_1)$]偱偁傞丅
$(A_1):$
傑偢丄検巕尵岅偲偄偆尵岅偑偁傞丅丂偟偐偟丄検巕尵岅偼宍帶忋妛偱丄懡彮偺僋儗乕僕乕偝傪撪憼偟偰偄傞丅
$(A_2):$
偙偺検巕尵岅傪暔棟妛偲尒側偟偰丄検巕椡妛傪嶌傝忋偘偨偲偡傞丅丂偙偺偲偒丄乽検巕尵岅偺尵岅揑僋儗乕僕乕偝(壓偺§9偵彂偔)乿偼夝徚偣偢偵丄
検巕椡妛偺夝庍(偨偲偊偽丄僐儁儞僴乕僎儞夝庍)偺僋儗乕僕乕偝偲偟偰巆偭偰偟傑偭偨丅
偱偁傞丅 偡側傢偪丄
\begin{align}
\overset{\mbox{ (尵岅揑僋儗乕僕乕偝)}}{
\underset{\mbox{ (宍帶忋妛, 尵岅)}}{
{\fbox{検巕尵岅}}
}
}
\xrightarrow[\mbox{暔棟壔}]{}
\overset{\mbox{ (僐儁儞僴乕僎儞夝庍偺僋儗乕僕乕偝)}}{
\underset{\mbox{ (暔棟妛)}}{
{\fbox{検巕椡妛}}
}
}
\tag{1}
\end{align}
偱偁傝丄扨側傞埨捈側暔棟壔偱偁偭偨偐傜偱偁傞偲峫偊傞丅(Fig. 1.1偺嘍偱姰惉偝傟傞偱偁傠偆検巕暔棟妛偼,
(1)幃偺傛偆側峔恾偱惗傑傟偨傕偺偱偼側偄偲怣偠傞).
§4. 検巕尵岅偺懍廗偺堊偵偼乽検巕尵岅亖検巕椡妛偺尵岅壔乿偲巚偊偽傛偄
傕偟検巕椡妛偺抦幆傪懡彮帩偭偰偄傞側傜偽丄乽検巕尵岅偺懍廗乿偵偼丄(1)幃偺媡傪峫偊傞偺堦斣
庤偭庢傝憗偄丅
偡側傢偪丄
\begin{align}
\overset{\mbox{ (懡彮偺尵岅揑僋儗乕僕乕偝)}}{
\underset{\mbox{ (宍帶忋妛, 尵岅)}}{
{\fbox{検巕尵岅}}
}
}
\xleftarrow[\mbox{尵岅壔丒偙偲傢偞壔}]{}
\overset{\mbox{ (僐儁儞僴乕僎儞夝庍偺僋儗乕僕乕偝)}}{
\underset{\mbox{ (暔棟妛)}}{
{\fbox{検巕椡妛}}
}
}
\tag{2}
\end{align}
偱偁傞丅
(2)幃偺堄枴傪愢柧偟傛偆丅
師偺椙偔抦傜傟偨(僐儁儞僴乕僎儞棳偺)検巕椡妛:
\begin{align}
&
\underset{\mbox{}}{\fbox{検巕椡妛}}
:=
\underbrace{
\underset{\mbox{ }}{
\overset{
[\mbox{ 儃儖儞}]
}{\fbox{検巕應掕應掕}}
}
\quad
+
\quad
\underset{\mbox{ }}{
\overset{
[{\mbox{ 僴僀僛儞儀儖僌, 僔儏儗乕僨傿儞僈乕}}]
}{\fbox{検巕塣摦曽掱幃}}
}
}_{\mbox{ (暔棟朄懃)}}
\quad
+
\quad
\underbrace{
\underset{\mbox{
}}
{
\overset{
{}}{\fbox{僐儁儞僴乕僎儞夝庍}}
}
}_{\mbox{ 暔棟朄懃偺巊偄曽偺儅僯儏傾儖}}
\tag{3}
\end{align}
傪尵岅壔(庺暥壔)偟偰丄師偺検巕尵岅傪偊傞丅
\begin{align}
&
\underset{\mbox{ (=検巕尵岅)}}{\fbox{應掕棟榑}}
:=
\underbrace{
\underset{\mbox{ ($\S$2.7)}}{
\overset{
[\mbox{尵岅儖乕儖1}]
}{\fbox{弮悎應掕}}
}
\quad
+
\quad
\underset{\mbox{ ($\S$10.3)}}{
\overset{丂
[{\mbox{ 尵岅儖乕儖2}}]
}{\fbox{場壥娭學}}
}
}_{\mbox{ 堦庬偺庺暥 (傾僾儕僆儕側憤崌敾抐)}}
\quad
+
\quad
\underbrace{
\underset{\mbox{
($\S$3.1)
}}
{
\overset{
{}}{\fbox{尵岅揑僐儁儞僴乕僎儞夝庍}}
}
}_{\mbox{ 庺暥偺巊偄曽偺儅僯儏傾儖}}
\tag{4}
\end{align}
検巕尵岅偼尵岅偱偁偭偰丄暔棟妛偱偼側偄丅偟偨偑偭偰丄忋偺尵岅儖乕儖 (i..e., 尵岅儖乕儖1偲2)偼暔棟朄懃偱偼側偄丅堦庬偺庺暥(偍宱, 宍帶忋妛揑柦戣)偱偁偭偰丄
幚尡専徹偡傞偙偲偼偱偒側偄丅
師偵尵岅儖乕儖偲2傪彂偄偰偍偙偆丅
§5. 尵岅儖乕儖1
師偼丄儃儖儞偺検巕應掕棟榑偺尵岅壔(庺暥壔丄偙偲傢偞壔丄悢妛揑堦斒壔)偱偁傞丅検巕椡妛偲嶌梡慺戙悢偺愱栧壠側傜偽丄捈偪偵棟夝壜擻偐傕偟傟側偄偑丄
偦偆偱側偄側傜偽丄懡彮偺弨旛偑昁梫偐傕偟傟側偄(壓偺曗懌傪嶲徠)丅
 尵岅儖乕儖1(應掕) 弮悎宯${\mathsf M}_{\overline{\mathcal A}} \big({\mathsf O}{},
S_{[\rho] }\big)$
尵岅儖乕儖1(應掕) 弮悎宯${\mathsf M}_{\overline{\mathcal A}} \big({\mathsf O}{},
S_{[\rho] }\big)$
偁傜備傞僔僗僥儉偼偁傞婎杮峔憿
$[ {\mathcal A} \subseteq \overline{\mathcal A}]_{B(H)}$撪偱掕幃壔偱偒傞.
$[ {\mathcal A} \subseteq \overline{\mathcal A}]_{B(H)}$
撪偱掕幃壔偝傟偨$W^*$-應掕
${\mathsf M}_{\overline{\mathcal A}} \big({\mathsf O}{{=}} (X, {\cal F} , F),
S_{[\rho] } \big)$
$\Big($
傑偨偼,
$C^*$-應掕}
${\mathsf M}_{{\mathcal A}} \big({\mathsf O}{{=}} (X, {\cal F} , F),
S_{[\rho] } \big)$
$\Big)$
傪
峫偊傛偆丏
偙偺偲偒,
$W^*$-應掕
${\mathsf M}_{\overline{\mathcal A}} \bigl({\mathsf O} , S_{[\rho] } \bigl)$
$\Big($
傑偨偼,
$C^*$-應掕
${\mathsf M}_{{\mathcal A}} \big({\mathsf O}{{=}} (X, {\cal F} , F),
S_{[\rho] } \big)$
$\Big)$
偵傛傝摼傜傟傞
應掕抣$ x$
$(\in X )$
偑丆
$ \Xi $
$(\in {\cal F})$
偵懏偡傞
妋棪
偼丆
\begin{align}
\rho( F(\Xi))
(\equiv _{{{\mathcal A}^*}}(\rho, F(\Xi) )_{\overline{\mathcal A}} )
\end{align}
偱梌偊傜傟傞
§6.尵岅儖乕儖2
師偼丄検巕塣摦曽掱幃偺尵岅壔(庺暥壔丄悢妛揑堦斒壔)偱偁傞丅
 尵岅儖乕儖 2 (場壥娭學)
尵岅儖乕儖 2 (場壥娭學)
$T$傪栘敿弴彉廤崌偲偡傞丅丂奺 $t (\in T)$偵懳偟偰, 婎杮峔憿 $[{\mathcal A}_t \subseteq \overline{\mathcal A}_t]_{ B(H_t)}$傪峫偊傞.
偙偺偲偒,
場壥娭學
偺楢嵔偼
場壥嶌梡慺楍
$ \{ \Phi_{t_1,t_2}: $
${\overline{\mathcal A}_{t_2}} \to {\overline{\mathcal A}_{t_1}} \}_{(t_1,t_2) \in T^2_{\leqq}}$
偵傛傝昞尰偝傟傞丏
§7. 検巕尵岅偺庡挘
偙偙偱,
偟偨偑偭偰丄乽棟夝乿偼晄梫偱偁傞丅
検巕尵岅偺庡挘偼丄
偱偁傞丅
偙偺庺暥偺尵梩尛偄偱彅尰徾傪婰弎偣傛!
$\quad$
乽擇偮偺尵岅儖乕儖乿傪娵埫婰偟偨側傜偽, 偁偲偼,丂幚愴偱偁傞丅
嵟弶偼,堄枴晄柧偵巚偆偐傕偟傟側偄偑,
偦偺偆偪忋払偟偰,
検巕尵岅傪巊偄偙側偣傞傛偆偵側傞. 偮傑傝丄
傑偨偼丄
§8. 墡傕栘偐傜棊偪傞

$\Large{\mbox{墡偑}}
\left\{\begin{array}{ll}
\Large{\mbox{峅朄戝巘}}
\\
\small{\mbox{(峅朄傕昅偺岆傝)}}
\\
\\
\Large{\mbox{壨摱}}
\\
\small{\mbox{(壨摱偺愳棳傟)}}
\\
\\
\cdots
\end{array}\right\}
\mbox{偵傕側傞}
$
検巕尵岅偺応崌偼丄丂Fig1.1偱帵偟偨傛偆偵丄
§9. 尵岅揑僐儁儞僴乕僎儞夝庍(=庺暥偺巊偄曽偺儅僯儏傾儖)偲偼壗偐丠
幃(3)偺暔棟妛偺僐儁儞僴乕僎儞夝庍(=暔棟朄懃偺巊偄曽偺儅僯儏傾儖)偺曽偼丄彫偝偄嶨懡側暔棟朄懃偺傛偆側傕偺偱丄
巊偆懁偱寛傔傜傞傛偆側傕偺偱偼側偔乽揤偐傜梌偊傜傟偨寛傑傝乿偱偁傞丅
堦曽丄幃(4)偺尵岅揑僐儁儞僴乕僎儞夝庍(=庺暥偺巊偄曽偺儅僯儏傾儖)偼丄庺暥偺桳梡惈偑廫暘偵敪婗偱偒傞傛偆偵
巊偆懁偑寛傔傟偽偄偄丅
偝偰丄忋偱弎傋偨傛偆偵丄
偟偨偑偭偰丄幃(4)偺尵岅揑僐儁儞僴乕僎儞夝庍(=庺暥偺巊偄曽偺儅僯儏傾儖)偼昁梫晄壜寚偲偄偆傢偗偱偼側偄偑丄
偁偭偨傎偆偑曋棙偱偁傞丅埲壓偵偙傟偵偮偄偰婔偮偐偺拲堄揰傪弎傋偰偍偔丅
偦偺偆偪忋払偟偰,
検巕尵岅傪巊偄偙側偣傞傛偆偵側傞.
僨僇儖僩恾幃3.1傪擮摢偵抲偄偰丄尵岅揑夝庍偲偄偆儅僯儏傾儖(B$_1$)-(B$_7$)偺壓偵丄
尵岅儖乕儖1偲2偺尵梩尛偄偱偡傋偰偺尰徾傪婰弎偣傛両
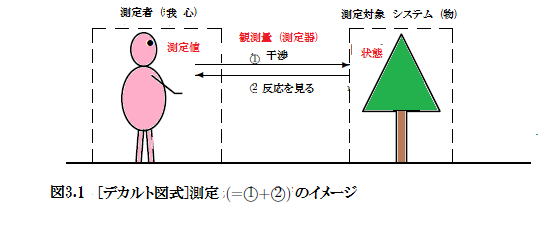
摍.
偄傠偄傠偲偁偭偰嶨懡側姶偠偑偡傞偐傕
偟傟側偄偑丆偦傟偼乽岞棟丒儖乕儖乿偲偄偆傛傝乽尵岅儖乕儖偺巊偄曽偺巜帵(儅僯儏傾儖)乿
偱偁傞偨傔偱,丂嵶偐偄偙偲傪尵偊偽,愗傝偑側偄.丂
$(B_1):$ 乽変(=應掕幰)乿偲乽暔(=應掕懳徾)乿偺俀偮偐傜惉傞
擇尦榑偱丆
摉慠丆
乽変(=應掕幰)乿偲乽暔(=應掕懳徾)乿
偼姰慡暘棧偱丄偙偺擇偮傪崿摨偟偰偼側傜側偄.
歡偊偰尵偆側傜偽丆
乽娤媞偼晳戜偵忋偑傜側偄乿
偱偁傞丅丂乽変乿偑乽変乿傪應掕偡傞側偳偲偄偆愝掕傪峫偊偰偼側傜側偄(cf. 8.4愡丗僐僊僩柦戣).
$(B_2):$
乽暔(=應掕懳徾)乿偺曽偵偼丆帪娫丒嬻娫傪憐掕偡傞偑丆
乽変(=應掕幰)乿偵偼丆帪娫丒嬻娫傪憐掕偟側偄丏
偟偨偑偭偰丆應掕棟榑偵偼丆乽應掕帪崗,應掕屻,應掕偟偨弖娫乿,乽帪惂乿偺奣擮偑側偄偺偱丆
應掕棟榑偱婰弎偝傟傞彅壢妛偵傕乽帪惂乿偺奣擮偼側偄
$(B_3):$
應掕偼,
乽変(=應掕幰)乿偲乽暔(=應掕懳徾)乿偺憡屳嶌梡[嘆偲嘇]偲僀儊乕僕偟偰傕傛偄偑丆
憡屳嶌梡偺偙偲傪梲偵偼尵傢側偄
$(B_4):$
應掕偼堦夞偩偗.丂
偟偨偑偭偰丄忬懺偼堦偮偩偗丄
偟偐傕丆
應掕屻偺忬懺偼峫偊側偄丏偮傑傝丄丂攇懇偺廂弅偼柍偄丅
$(B_5):$
應掕側偔偟偰丆妋棪側偟
$(B_6):$
忬懺偼曄壔偟側偄.丂偟偨偑偭偰丄僔儏儗乕僨傿儞僈乕昤憸偼峫偊偢丄僴僀僛儞儀儖僌昤憸偟偐峫偊側偄丅
傑偨,杮彂偺庡挘(忋偺§2 偺嘒)偼
側偺偱丄
偲巚偭偰傕傛偄偩傠偆.
(B$_7$)偼怣偠擄偄婏愓偱偁傞偑,
$(B_7):$ 僊儕僔儍埲棃偺揘妛幰偨偪偺嬥尵偺懡偔偼,尵岅揑僐儁儞僴乕僎儞夝庍偺堦晹偵側偭偰偄傞
$(C):$ 僨僇儖僩=僇儞僩揘妛偲検巕尵岅偼嫟偵丄栚揑偼悽奅婰弎偱偁傝丄偦偺曽朄偼
擇尦榑揑娤擮榑(怱恎擇尦榑丒暔怱擇尦榑丒宍帶忋妛)偱摨偠側偺偩偐傜丄
偲峫偊側偄曽偑偍偐偟偄丅偡傋偰偺揘妛幰偑攏幁偲偄偆偙偲傕側偄偩傠偆丅
傕偪傠傫丄僨僇儖僩亖僇儞僩揘妛偼幐攕偟偨傢偗偩偑丄偦偺攕場偼丄乽尵岅乿偱側偔偰乽擣幆乿傪捛媶偟偨偙偲偱丄丂旂擏傪崬傔偰尵偆側傜偽丄乽尵岅儖乕儖乿傪抦傜偢偵丄偦偺巊偄曽偺儅僯儏傾儖傪捛媶偟偨偙偲偩傠偆丅
偝偰丄
偦偺偆偪忋偺$(B_1) \sim (B_7)$摍傪夛摼偟偰,検巕尵岅傪巊偄偙側偣傞傛偆偵側傞.
傪妝娤揑偲巚偆偐傕偟傟側偄偑丄帋峴嶖岆偱挊幰偼$(B_1) \sim (B_7)$摍傪夛摼偟偨丅丂傕偪傠傫丄壜擻惈偲偟偰偼丄
偼怱攝偵側傞丅崱偺偲偙傠丄塃偺僒僀僪僶乕[栚師]掱搙偺偙偲偼僇僶乕偟偰偄傞偲偟偐尵偊側偄偑丄妝娤揑偵乽偦偺偲偒偼丄$(B_8)$傪
晅偗壛偊傟偽偄偄乿偲巚偭偰偄傞丅
$(D):$
尵岅揑僐儁儞僴乕僎儞夝庍偱僇僶乕偱偒側偄検巕尰徾丒僷儔僪僢僋僗偑偁傞偐傕偟傟側偄
側偺偩偐傜丄乽(暔棟揑偵)偄偐偑傢偟偄乿偙偲傪婥偵偡傞偙偲偼側偄丅宍帶忋妛偲偼丄乽婥妝側傕偺乿偱偁傞丅
偵夝摎傪梌偊傞丅
- 検巕尵岅偼巊傢傟側偗傟偽堄枴偑側偄
偐傜偱丄宍帶忋妛傕娒偄傢偗偱偼側偄丅丂偟偐偟丄偙傟偼戝忎晇偩傠偆丅丂検巕椡妛偲摑寁妛偺椉曽傪崌傢偣偨偖傜偄僷儚僼儖側偺偩偐傜丅
曗懌
棟岺宯偺戝妛懖側傜偽丄悢妛偺僸儖儀儖僩嬻娫榑偺弶曕(悢妛壢4擭掱搙)傪妛傋偽丄乽尵岅儖乕儖1偲2乿傪撉傔傞傛偆偵側傞偩傠偆丅偟偐偟丄杮彂傪撉傓応崌偼丄娙扨側椺傪懡悢梡堄偟偰偄傞偺偱丄偦偺椺傪捠偟偰乽尵岅儖乕儖1偲2乿偵姷傟偰偄偗偽傛偄丅偨偲偊偽丄杮彂 § 5.5偺乽儌儞僥傿丒儂乕儖栤戣乿側偳崱偱傕偡偖撉傔偰丄應掕偺宍帶忋妛揑懁柺傪捈偪偵棟夝偱偒傞偲巚偆丅
検巕椡妛偺懡彮偺抦幆傪帩偭偰偄傞撉幰側傜偽丄師偺暥專傪愭偵撉傓偙偲傪姪傔傞丗
| [1]: | S. Ishikawa, 乬A New Interpretation of quantum mechanics,Journal of Quantum Information Science,乭 Vol. 1 No. 2, 2011, pp. 35-42. doi: 10.4236/jqis.2011.12005 ( download free) |
| [2]: | S. Ishikawa, 乬Quantum mechanics and the Philosophy of Language: Reconsideration of Traditional Philosophies," Journal of quantum information science, Vol. 2, No. 1, 2012, pp.2-9.doi: 10.4236/jqis.2012.21002 ( download free) |
| [3]: | S. Ishikawa,丂The linguistic nterpretation of quantum mechanics; quantum mechanics,乭arXiv:1204.3892v1[physics.hist-ph], (2012) ( download free) |
検巕椡妛偺娤應丒夝庍栤戣偼條乆側娤揰偐傜尋媶偝傟傞傋偒偙偲偼摉慠偱偁傞偑丄嵟傕挧愴偡傞壙抣偺偁傞栤戣偼
| $(\sharp):$ | 幩塭壖愢(=攇懇偺廂弅)偺柍偄夝庍傪尒偮偗弌偡偙偲 |
偱偁傞偲挊幰偼怣偠偰偄傞丅 傕偪傠傫丄昗弨揑僐儁儞僴乕僎儞夝庍偑偍悽帿偵傕旤偟偄偲偼尵偊側偄幩塭壖愢傪嵦梡偟偰偄傞偺偵偼丄偦傟側傝偺棟桼偑偁傞偺偩偲巚偆丅
偟偐偟丄検巕椡妛偵偼丄壗偑婲偙傞偺偐梊憐偱偒側偄柺敀偝偑偁傞丅検巕椡妛偺楌巎偺拞偱偼丄扤傕偑怣偠偰偄偨偙偲偑斲掕偝傟偨偙偲側偳枃嫇偵偄偲傑偑側偄丅 偦偆峫偊偰丄挊幰偼(幩塭壖愢(=攇懇偺廂弅)偺柍偟偺)検巕尵岅傪採彞偟偨丅丂杮彂偱帵偟偨傛偆偵丄検巕尵岅偼嫮椡側婰弎椡傪桳偡傞偺偱丄 攋抅偡傞壜擻惈偼彮側偄偲怣偠傞偑丄傗偼傝懡偔偺尋媶幰偺僠僃僢僋偑昁梫偩傠偆丅丂崱屻丄崕暈偱偒側偄傪崲擄傪抦偭偨偲偒偵偼丄捈偪偵偙偺応偱曬崘偡傞丅
